Механические колебания. Гармонические колебания. Дифференциальное уравнение гармонических колебаний материальной точки презентация
Содержание
- 2. МАТЕМАТИЧЕСКАЯ СПРАВКА Большинство реальных колебательных процессов не являются строго периодическими. Однако, экспериментально любые сложные колебания можно
- 3. Теоретически сложные колебания можно представить с помощью рядов (и интегралов) Фурье. Согласно теореме Ж. Фурье (1822
- 4. Согласно теории рядов Фурье, всякая периодическая функция f(t), ограниченная на отрезке и имеющая конечное число экстремумов
- 5. Для четной функции f(-t)= f(t) все коэффициенты ак равны нулю. Для нечетной ф -ии f(-t)= -
- 6. Для решения этой задачи могут использоваться комплексные ряды Фурье в виде: ( 5 ) где п
- 7. В разложении (5) представлен дискретный спектр частот: Непериодическая функция f(t) представляется в виде комплексного интеграла Фурье:
- 8. Когда частоты колебаний неодинаковые, то при различных амплитудах и начальных фазах получается сложное колебание, как это
- 9. Разложение сложного колебательного движения на составляющие простые гармоники с кратными частотами: 1—1,— основная гармоника ( β1
- 10. По теореме Фурье любую периодическую функцию можно представить в виде суммы нескольких гармонических функций с кратными
- 11. Сложный периодический процесс, например ряд чередующихся импульсов затухающих колебаний от периодических толчков (биение вала), представляется сериальным
- 12. Отдельный апериодический, затухающий импульс от удара (непериодическая функция времени) представляется сплошным, или непрерывным, спектром, т. е.
- 13. В зависимости от характера воздействия, вызывающего и поддерживающего колебательный процесс, колебания классифицируют как свободные (или собственные),
- 14. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Гармонические колебания представляют собой наиболее простой вид колебаний. Пусть х — динамическая переменная, характеризующая
- 15. А — амплитуда колебаний, т. е. наибольшее положительное отклонение величины х от ее значения в состоянии
- 16. Величины ϕ = ωt +ϕ01 и ϕ = ωt +ϕ02 называются фазами колебаний. Фаза характеризует текущее
- 17. Произвольное гармоническое колебание может быть представлено и иным образом. Преобразуем ,например, х = Аsin (ωt +
- 19. Решение многих вопросов, в частности, сложение нескольких колебаний одинакового направления, облегчается и становится наглядным, если изображать
- 20. Для этого из точки О, взятой на оси х, под углом φ откладывается вектор А, модуль
- 21. По характеру изменения амплитуды различают незатухающие, затухающие, нарастающие , амплитудно-модулированные колебания , а также частотно-модулированные колебания.
- 22. 3) Период Т = 1/γ, с, − длительность полного колебания. 4)Число колебаний к моменту времени t
- 24. Для гармонического движения системы мгновенная скорость Мгновенное ускорение колебательной системы определяется второй производной s = Acosφ
- 25. 2.Энергия гармонического колебания Энергия системы, колеблющейся без затухания,постоянна .Она складывается из кинетической Ек и потенциальной Еп
- 26. 3. Гармонический и ангармонический осциллятор Пружинный маятник является примером свободного механического осциллятора,без энергетических потерь Математический маятник
- 27. Наряду с гармоническим осциллятором существует понятие ангармонического (нелинейного) осциллятора. Его колебания отличаются от гармонических. Их основная
- 28. Разность фаз δ не зависит от времени и равна
- 29. Когда |ω1–ω2| Результирующее колебание, с медленно и периодически меняющейся амплитудой, называется биения. Амплитуда колебаний описывается формулой
- 30. Промежуток времени между соседними моментами, когда амплитуда а максимальна , называют периодом биений τ б. За
- 31. 2)Сложение взаимно перпендикулярных колебаний одинаковой частоты
- 32. Фигура Лиссажу есть траектория, получаемая от соединения линией результирующих смещений в различные моменты времени на плоскости
- 33. Если частоты взаимно перпендикулярных колебаний не одинаковы и относятся как целые числа, то траектории результирующего движения
- 34. Фигуры Ж. Лиссажу можно наблюдать при подаче на пластины осциллографа двух электрических сигналов, один из которых
- 35. При сложении взаимно-перпендикулярных колебаний полная энергия т. е. складывается из энергий каждого колебания (в отличие от
- 36. Fx= – r , Из основного уравнения динамики следует, что на частицу массы m действует кроме
- 37. Это уравнение при условии β где а0 и α — постоянные, определяемые начальными условиями х (0)
- 38. Энергия затухающих колебаний Эта энергия складывается из потенциальной и кинетической: После подстановки сюда выражений х (t)
- 39. Характеристики затухания. Кроме коэффициента β , затухание колебаний характеризуют величинами: 1) Время релаксации — это время,
- 40. 3) Добротность осциллятора − При малом затухании β«ω0 добротность равна Логарифмический декремент затухания λ (при малом
- 41. Вынужденные колебания.Уравнение вынужденных колебаний Потери энергии, обусловленные силами сопротивления (трения), можно компенсировать, воздействуя на систему переменной
- 42. Если на колеблющуюся частицу будут действовать одновременно три силы:квазиупруггая ( − kx ), сила сопротивления (
- 43. Опыт показывает, что по истечении некоторого времени с момента начала действия вынуждающей силы в системе устанавливаются
- 44. Учитывая фазовые сдвиги между х, и , представим это равенство с помощью векторной диаграммы для случая
- 45. по теореме Пифагора =
- 46. Резонанс На рисунке приведены графики зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы а(ω) для трех
- 47. Зависимость фазового сдвига φ от частоты ω показана для двух значений коэффициента затухания β .
- 48. Среднее значение мощности колебаний за период равно максимально-му значению при ω = ω0 независимо от коэффициента
- 49. Энергия вынужденных колебаний. Так как Е = U+ К , то учтено, что
- 50. График зависимости E(t) для случая ω > ω0 показан на следующем рисунке. Амплитуда колебаний энергии Е
- 51. Зависимость полной энергии механической системы от времени , – диссипативная функция , − мощность внешнего источника
- 53. Скачать презентацию
 Природа света. Законы отражения и преломления света. Законы освещенности. Урок №22
Природа света. Законы отражения и преломления света. Законы освещенности. Урок №22 Ремонтный процесс Standox Nissan KAB Ultimate Metal Silver. Тренинговая информация
Ремонтный процесс Standox Nissan KAB Ultimate Metal Silver. Тренинговая информация Подъемно-транспортное оборудование
Подъемно-транспортное оборудование Деление ядер урана. Цепные ядерные реакции
Деление ядер урана. Цепные ядерные реакции Знакомство с бытовой швейной машиной
Знакомство с бытовой швейной машиной Айнымалы ток
Айнымалы ток Молекулярна фізика. Явища переносу в газах
Молекулярна фізика. Явища переносу в газах Параллельное и последовательное соединение
Параллельное и последовательное соединение Спектроскопические методы анализа. Методы атомной и молекулярной спектроскопии
Спектроскопические методы анализа. Методы атомной и молекулярной спектроскопии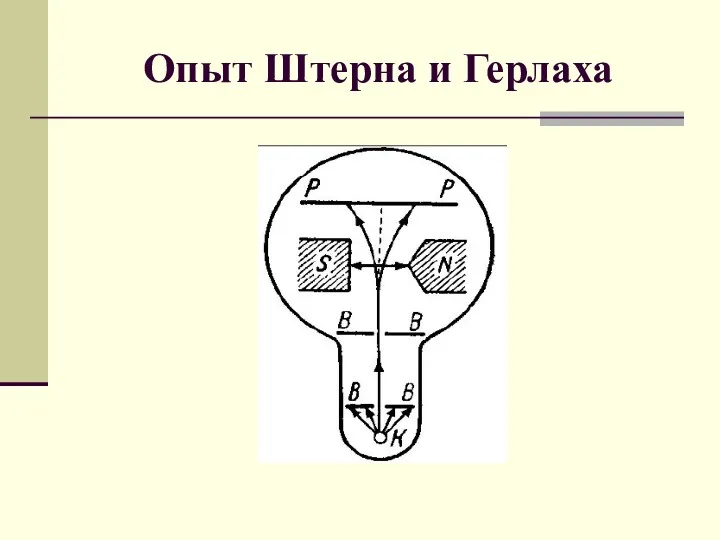 Опыт Штерна и Герлаха
Опыт Штерна и Герлаха Двигатель танка Т-72
Двигатель танка Т-72 Клиновые и шлифтовые соединения
Клиновые и шлифтовые соединения Простые механизмы и их использование в машинах
Простые механизмы и их использование в машинах Радиотелескоп
Радиотелескоп Эксперимент. Что такое эксперимент?
Эксперимент. Что такое эксперимент? Поршеньді компрессорларды жөндеу
Поршеньді компрессорларды жөндеу Возникновение атомистической гипотезы строения вещества и ее экспериментальные доказательства. Идеальный газ
Возникновение атомистической гипотезы строения вещества и ее экспериментальные доказательства. Идеальный газ Энергия. Виды энергии
Энергия. Виды энергии Методы и средства наблюдения и контроля за состоянием природной среды
Методы и средства наблюдения и контроля за состоянием природной среды Организация технического обслуживания и ремонта автомобиля Урал-4320
Организация технического обслуживания и ремонта автомобиля Урал-4320 Лекция 3. Работа pn-перехода. pn-переход в состоянии термодинамического равновесия
Лекция 3. Работа pn-перехода. pn-переход в состоянии термодинамического равновесия Механизм газораспределения
Механизм газораспределения Буксовый узел электровоза ВЛ-11
Буксовый узел электровоза ВЛ-11 Детали машин и основы конструирования. Цепные передачи. (Лекция 6)
Детали машин и основы конструирования. Цепные передачи. (Лекция 6) Линзы. Ход лучей в линзах
Линзы. Ход лучей в линзах Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Давление твердых тел. Единицы давления. 7 класс
Давление твердых тел. Единицы давления. 7 класс Явище поляризація світла. Оптична активність речовин
Явище поляризація світла. Оптична активність речовин