Содержание
- 2. Вступление Многие не знают, что такое матрица, но еще больше людей не знают, как применять матричный
- 3. Матрица представляет собой математический объект, который записывается в формате прямоугольной таблицы с элементами внутри. Впервые матрица
- 4. Цель исследовательской работы: рассмотреть матричную алгебру в экономике на примере решения задач адаптированных к социально-экономическим реалиям
- 5. Линейная алгебра Линейная алгебра – это раздел математики, в рамках которого изучаются самые разнообразные объекты линейной
- 6. Что такое матрицы и операции над ними? Прямоугольная таблица А, содержащая m строк и n столбцов,
- 7. Существуют основные операции над матрицами. Сложение (вычитание). Эта операция определена для матриц происходит сложение (вычитание) их
- 8. Существуют основные операции над матрицами. . Пример: Найти произведение матриц A = и B = Решение:
- 9. Существуют основные операции над матрицами. Транспонирование. Для того чтобы транспонировать матрицу необходимо сформировать новую матрицу, обозначается
- 10. Ранг матрицы Рангом матрицы А называется наибольший из порядков ее миноров, не равных нулю. Обозначается ранг
- 11. Определитель матрицы Определитель матрицы или детерминант матрицы - это одна из основных численных характеристик квадратной матрицы,
- 12. Метод Крамера Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель
- 13. Метод Гаусса Иногда он также называется методом исключения. Условно состоит из двух этапов. Первый из них,
- 14. Пример решения задания методом Крамера Пример. Решить систему уравнений, используя правило Крамера. Решение. Найдем главный определитель
- 15. Пример решения задания методом Гаусса Пример. Решить систему уравнений, используя правило Гаусса. Решение: Переставив первое и
- 16. Решение задач по экономике с помощью матриц Типография производит печать продукции трех видов: газеты, журналы, книги.
- 17. Выводы В своей работе я доказала, что матрицы могут быть применимы в обыденной жизни, что алгебра
- 19. Скачать презентацию
 Презентация к уроку математики по теме Периметр прямоугольника
Презентация к уроку математики по теме Периметр прямоугольника Решение показательных уравнений и неравенств
Решение показательных уравнений и неравенств Кайсы фигура артык?
Кайсы фигура артык? Проверка качества уравнения регрессии
Проверка качества уравнения регрессии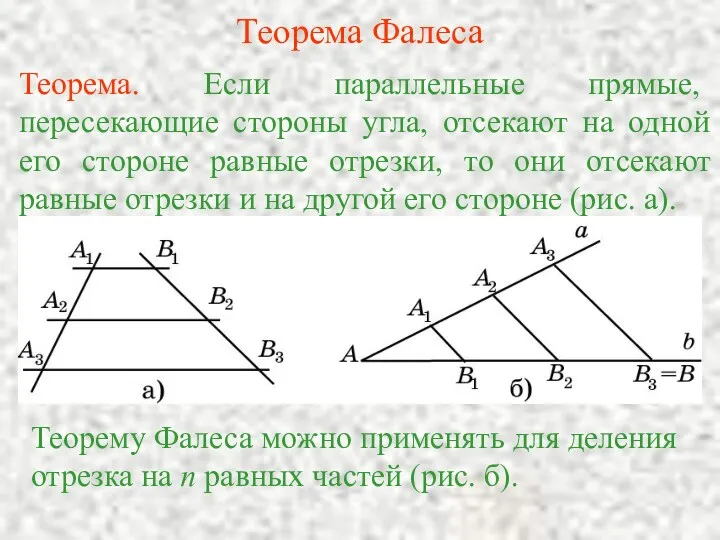 Теорема Фалеса
Теорема Фалеса Решение задач на составление уравнений
Решение задач на составление уравнений Подготовка к ОГЭ по геометрии
Подготовка к ОГЭ по геометрии Умножение на однозначное число
Умножение на однозначное число Расстояние от точки до фигуры
Расстояние от точки до фигуры Табличное умножение и деление.
Табличное умножение и деление. Математическая раскраска Колобок
Математическая раскраска Колобок Забавная арифметика
Забавная арифметика Урок -презентация по математике по теме Проценты в 5 кл.
Урок -презентация по математике по теме Проценты в 5 кл. Задачи на части и проценты
Задачи на части и проценты Способы задания и свойства числовых последовательностей
Способы задания и свойства числовых последовательностей Число и цифра 6.
Число и цифра 6. Задачи с практическим содержанием по теме: Решение треугольников 9 класс
Задачи с практическим содержанием по теме: Решение треугольников 9 класс Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32)
Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32) Решение задач.
Решение задач. Тренажер по математике для учащихся 1 класса Приключение богатырей
Тренажер по математике для учащихся 1 класса Приключение богатырей Положительные и отрицательные числа
Положительные и отрицательные числа Геометрическая интерпретация комплексных чисел
Геометрическая интерпретация комплексных чисел Пентамино
Пентамино Урок закрепления по теме : Сложение и вычитание вида +1,-1.
Урок закрепления по теме : Сложение и вычитание вида +1,-1. Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Задачи по геометрии
Задачи по геометрии Письменные приёмы сложения
Письменные приёмы сложения Формализм задачи линейной оптимизации на примере транспортной задачи
Формализм задачи линейной оптимизации на примере транспортной задачи