Содержание
- 2. 1. Логические функции Логический нуль – лог.0 Логическая единица – лог.1 Функции алгебры логики – функция
- 3. Способы задания логических функций Два способа Аналитический Запись формулой Табличный Таблицы значений функции
- 4. Способы задания логических функций Функция алгебры логики одного или двух аргументов, в логическом выражении которой содержится
- 5. Элементарные функции Существуют 4 элементарных функции алгебры логики 1 аргумента и 16 элементарных функций 2-х аргументов.
- 6. Элементарные функции Таблица истинности функций двух аргументов
- 7. 4 функции одного аргумента 1) f0(x) = 0 – константа нуля Реализуется генератором нуля - соединение
- 8. Таблица истинности функций двух аргументов
- 9. 2. Основные логические операции И – логическое умножение, ИЛИ – логическое сложение, НЕ – логическое отрицание.
- 10. Логическое сложение (дизъюнкция) Таблица истинности: Обозначение: ∨, + УГО: Реализуется логическим элементом ИЛИ
- 11. Логическое умножение (конъюнкция) Реализуется логическим элементом И Таблица истинности: Обозначение: & , ∧, · , x
- 12. Логическое отрицание (инверсия) Реализуется логическим элементом НЕ Таблица истинности: УГО: Обозначение: ¬A, Ā. Если А –
- 13. Стрелка Пирса Реализуется логическим элементом ИЛИ-НЕ. Таблица истинности: Обозначение: X ↓ Y, УГО: 1
- 14. Штрих Шеффера Реализуется логическим элементом И-НЕ. Таблица истинности: Обозначение: X | Y , УГО:
- 15. Исключающее ИЛИ (сложение по модулю 2) Таблица истинности: Обозначение: X Y УГО: + =1
- 16. Логическая равнозначность (эквиваленция) Таблица истинности: УГО: =1 Обозначение: ≡ , ↔,
- 17. Импликация Таблица истинности: Обозначение: →, ⊃ A → B = Y A ⊃ B = Y
- 18. Условно-графическое обозначение x1 x2 x3 F=x1⋅x2⋅x3= = x1∧x2∧x3 & & 1 x1 x3 x2 x4 x1
- 19. Приоритет выполнения логических операций (если нет скобок)
- 20. Пример Упростить заданное выражение: A∨B∧C→C∧A~B ⊕ C⊕A Последовательность выполнения логических операций: (((A)∨(B∧C))→(C∧A))~((B⊕C)⊕A) 1 3 2 5
- 21. Алгоритм построения таблиц истинности для сложных выражений Определить количество строк: количество строк = 2n + строка
- 22. Пример Составить таблицу истинности логического выражения: D = А ∧ (B ∨ C). Решение. Определить количество
- 23. Заполнить столбцы с учетом таблиц истинности логических операций.
- 24. Доказать справедливость тождества A ˅ B ˄ C = (A ˅ B) ˄ (A ˅ C)
- 25. Алгоритм построение логических схем Определить число логических переменных. Определить количество базовых логических операций и их порядок.
- 26. Логическая функция: Y = a ˅ b ˄ c Логическая схема для данной функции: Алгоритм построение
- 27. Пример Определить сигнал на выходе 1 0 1 1 1 1 1 1 1 0 1
- 28. 3. Свойства логических операций. Аксиомы алгебры логики Конъюнкция 0 ˄ 0 = 0 0 ˄ 1
- 29. Свойства логических операций. Теоремы алгебры логики 1. Теоремы исключения констант х ∨ 1 = 1 х
- 30. Свойства логических операций. Законы алгебры логики 1. Сочетательный (ассоциативный) х1 ˅ (х2 ˅ х3) = (х1
- 31. 4. Законы де Моргана (Закон общей инверсии) х1 ˅ х2 = х1 ˄ х2 х1 ˅
- 32. Формулы де Моргана Левая часть обращается в лог.1 только в том случае, если: Для этого: и
- 33. Правило применения формул де Моргана Инверсия любого сложного выражения, в котором аргументы (либо их инверсии) связаны
- 34. 4. Выражение элементарных функций через операции И, ИЛИ, НЕ. Операция запрета
- 35. Выражение элементарных функций через операции И, ИЛИ, НЕ. Сумма по модулю 2
- 36. Выражение элементарных функций через операции И, ИЛИ, НЕ. Операция ИЛИ-НЕ
- 37. Выражение элементарных функций через операции И, ИЛИ, НЕ. Логическая равнозначность Импликация
- 38. Выражение элементарных функций через операции И, ИЛИ, НЕ. Операция И-НЕ
- 39. 5. Базис Базис – набор простейших логических функций, позволяющих реализовать любую другую логическую функцию. Минимальный базис
- 40. Базис И-НЕ: ИЛИ-НЕ:
- 41. Минимизация логических функций
- 42. Этапы синтеза 1. Синтез комбинационных цифровых устройств
- 43. Дизъюнктивная нормальная форма (ДНФ) содержит элементарные конъюнкции, связанные между собой операцией дизъюнкции. 2. Совершенная дизъюнктивная нормальная
- 44. 2. Совершенная дизъюнктивная нормальная форма (СДНФ) нет двух одинаковых элементарных конъюнкций; ни одна элементарная конъюнкция не
- 45. Переход от ДНФ к СДНФ Для перехода от ДНФ к СДНФ необходимо в каждый из членов,
- 46. Переход от ДНФ к СДНФ Пример
- 47. Правило записи СДНФ по таблице истинности Выделить в таблице истинности все наборы переменных, на которых функция
- 48. Конъюнктивная нормальная форма (КНФ) содержит элементарные дизъюнкции, связанные между собой операцией конъюнкции. 3. Совершенная конъюнктивная нормальная
- 49. нет двух одинаковых элементарных конъюнкций; ни одна элементарная конъюнкция не содержит двух одинаковых переменных; ни одна
- 50. Переход от КНФ к СКНФ Для перехода от ДНФ к СДНФ необходимо в каждый из членов,
- 51. Правило записи СКНФ по таблице истинности Выделить в таблице истинности все наборы переменных, на которых функция
- 52. 4. Минимизация логических функций методом карт Вейча Для функций двух аргументов Для функций трех аргументов Для
- 53. Правила получения минимальной дизъюнктивной нормальной формы (МДНФ) Все клетки, содержащие 1, объединяются в замкнутые области. При
- 54. 4. Минимизация логических функций методом карт Вейча Таблица истинности для логической функции 1. Карта Вейча 2.
- 55. 4. Минимизация логических функций методом карт Вейча. Примеры Записать МДНФ для функции, заданной картой Вейча 1)
- 56. Синтез логических устройств в базисах ИЛИ-НЕ, И-НЕ
- 57. Синтез логического устройства в базисе ИЛИ-НЕ, реализующего функцию в таблице: Карта Вейча: Минимальная КНФ функции: Функция
- 58. Схема логического устройства
- 59. Синтез логического устройства в базисе И-НЕ, реализующего функцию в таблице: Карта Вейча: Минимальная ДНФ функции: Функция
- 60. Схема логического устройства
- 62. Скачать презентацию
 Парная линейная регрессионная модель
Парная линейная регрессионная модель Решение задач по темам Нахождение числа по его дроби, Нахождение дроби от числа
Решение задач по темам Нахождение числа по его дроби, Нахождение дроби от числа Геометрия мәселелері
Геометрия мәселелері Шар в задачах ЕГЭ
Шар в задачах ЕГЭ Сокращение дробей. Задание для устного счета. Упражнение 6. 6 класс
Сокращение дробей. Задание для устного счета. Упражнение 6. 6 класс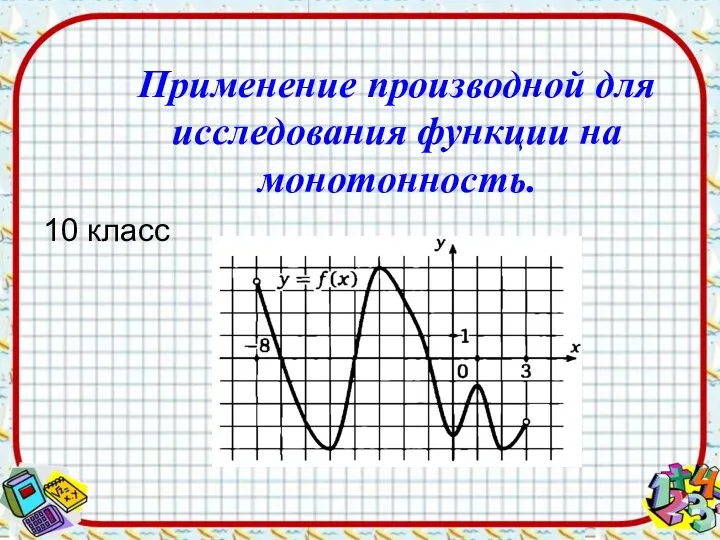 Применение производной для исследования функции на монотонность
Применение производной для исследования функции на монотонность УМК Возможности системы заданий учебников по математике (1-4 классы) для формирования и развития основ логического мышления
УМК Возможности системы заданий учебников по математике (1-4 классы) для формирования и развития основ логического мышления 20231120_skalyarnoe_proizvedenie_vektorov_v_prostranstve
20231120_skalyarnoe_proizvedenie_vektorov_v_prostranstve Освобождение от иррациональности в знаменателе дроби
Освобождение от иррациональности в знаменателе дроби Презентация Задачи осени. Диск
Презентация Задачи осени. Диск Составление числовых выражений с презентацией. УМК Начальная школа 21 века.
Составление числовых выражений с презентацией. УМК Начальная школа 21 века. Математика. 1 класс. Урок 35. Числа 1-6 - Презентация
Математика. 1 класс. Урок 35. Числа 1-6 - Презентация Вагоны и вагонное хозяйство. Надёжность подвижного состава. Статистическое толкование показателей надёжности. (Тема 4)
Вагоны и вагонное хозяйство. Надёжность подвижного состава. Статистическое толкование показателей надёжности. (Тема 4) Методика изучения геометрических величин. Лекция №6
Методика изучения геометрических величин. Лекция №6 Воспитание гражданина на уроках математики
Воспитание гражданина на уроках математики Обыкновенные дроби. Смешанные числа
Обыкновенные дроби. Смешанные числа Освоение величин в дошкольном возрасте как условие познания окружающего мира
Освоение величин в дошкольном возрасте как условие познания окружающего мира Қалпына келетін жуйелер. Интегродифференциалды сенімділік теңдігі
Қалпына келетін жуйелер. Интегродифференциалды сенімділік теңдігі Зачет по теме Квадратные уравнения
Зачет по теме Квадратные уравнения Урок по математике Деление круглых чисел 3 класс ОС Школа 2000...
Урок по математике Деление круглых чисел 3 класс ОС Школа 2000... Задачи на движение ( схемы)
Задачи на движение ( схемы) Неопределенный интеграл
Неопределенный интеграл Сложение вида: +4, +5. 1 класс
Сложение вида: +4, +5. 1 класс Применение производной к исследованию функции. Задания В9, В15 ЕГЭ
Применение производной к исследованию функции. Задания В9, В15 ЕГЭ Тест по теме: Перпендикулярные прямые в пространстве. Перпендикулярность прямой и плоскости
Тест по теме: Перпендикулярные прямые в пространстве. Перпендикулярность прямой и плоскости Неравенства с одной переменной
Неравенства с одной переменной Итоговый тест по математике (2 класс)
Итоговый тест по математике (2 класс) Разложение разности квадратов на множители
Разложение разности квадратов на множители