Однако, при решении обратной задачи можно поступить по-другому. Для этого составляют
обратную зависимость, считая заданное значение данной функции аргументом этой зависимости. Сделать это можно двумя способами:
Выразить из формулы данной функции х через у. В нашем случае:
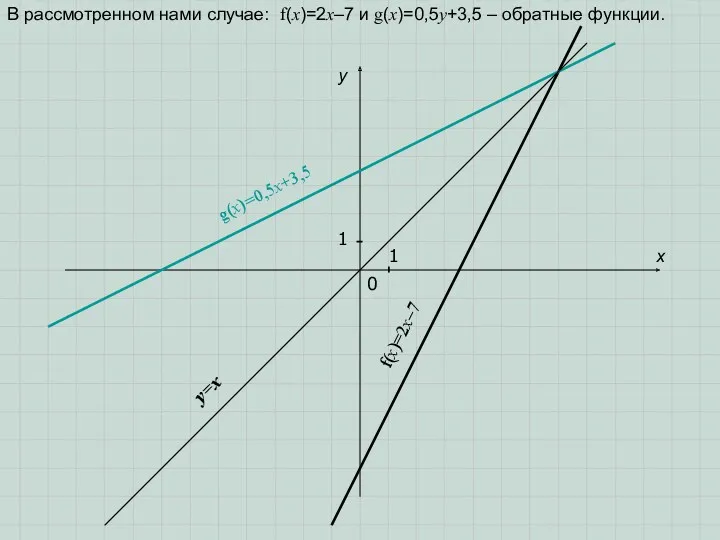
y=2x–7 ⇒ 2х=у+7 ⇒ х=0,5у+3,5. А теперь записать эту зависимость, как новую функцию, в привычном для нас виде: у=0,5х+3,5. Или
2) Поменять в формуле данной функции х и у. В нашем случае:
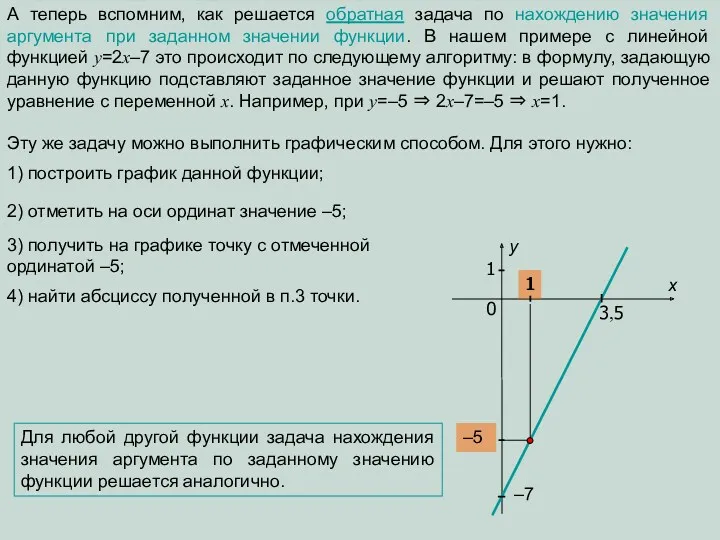
y=2x–7 ⇒ х=2у–7. А теперь записать эту зависимость, как новую функцию, в привычном для нас виде, выразив у через х : 2у=х+7 ⇒ у=0,5х+3,5.
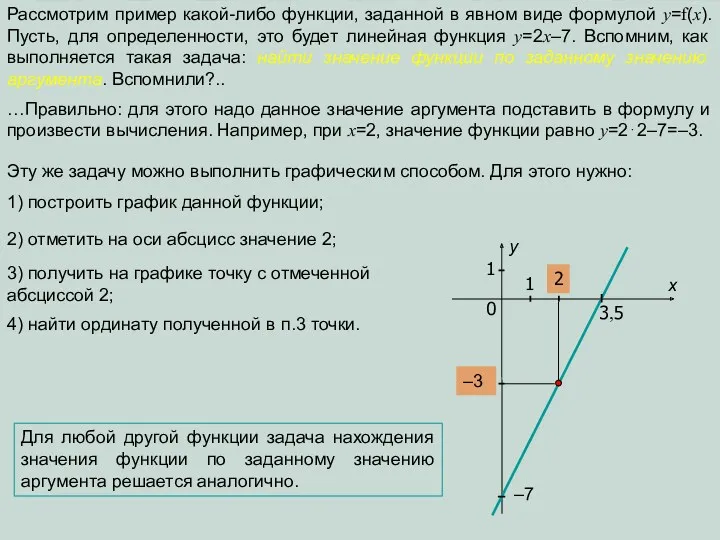
умножить на 2 и вычесть 7
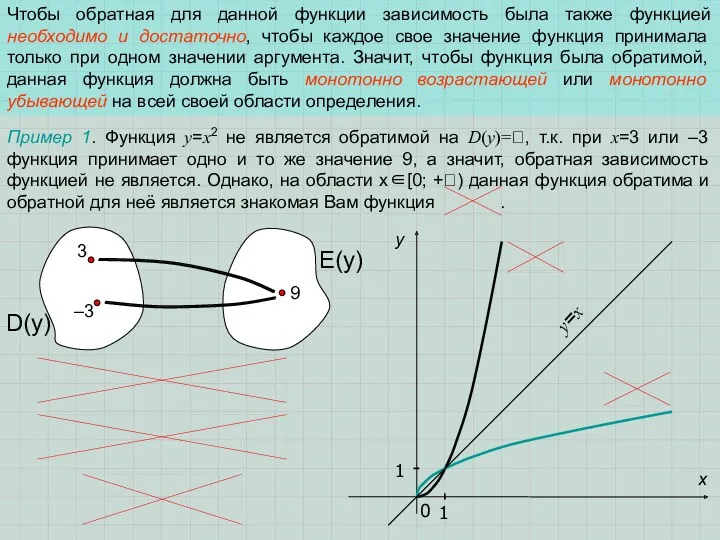
D(y) - область определения.
E(y) - область значений.
y=2x–7
прибавить 7 и разделить на 2.
D(y) - область определения
E(y) - область значений


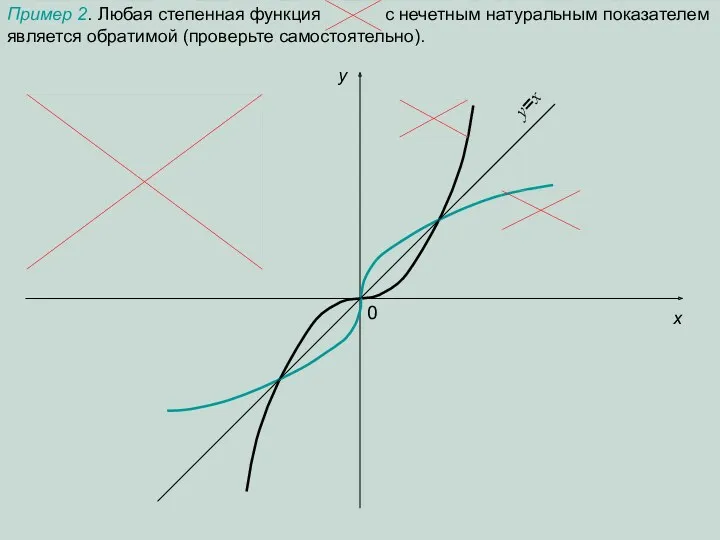

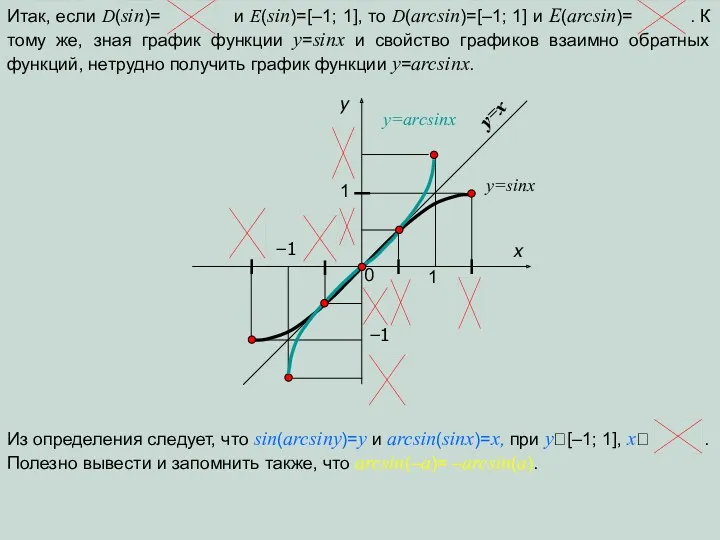
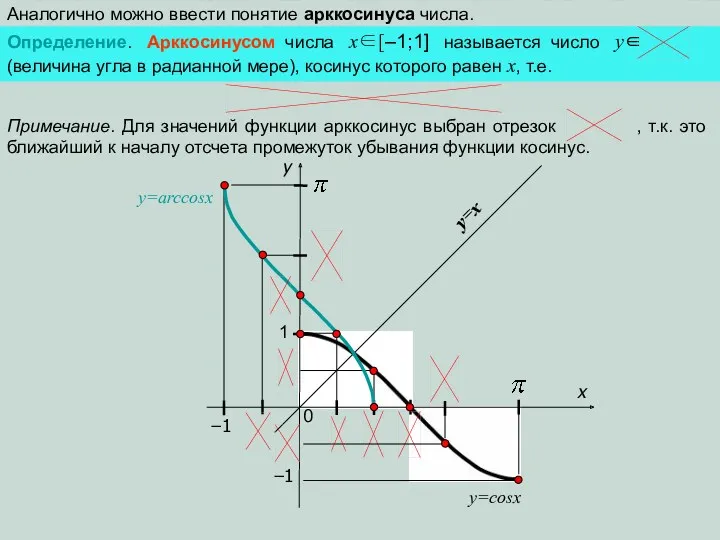
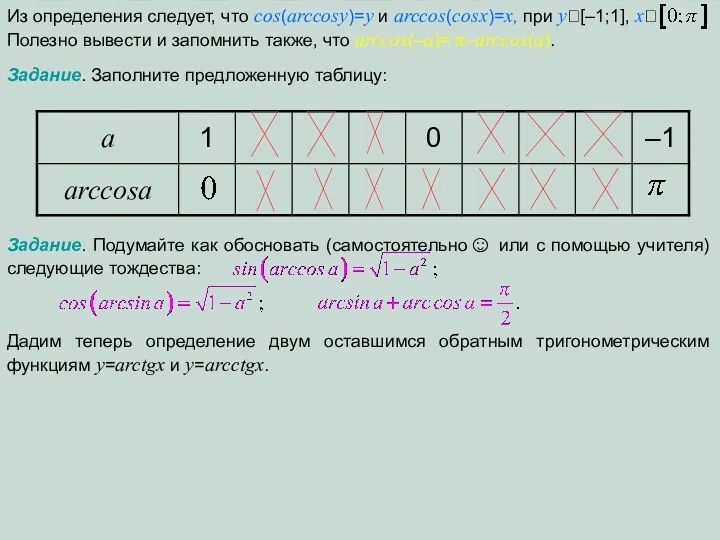
 Графическое изображение прямолинейного равноускоренного движения (презентация)
Графическое изображение прямолинейного равноускоренного движения (презентация) Урок по алгебре Квадратные уравнения 8 класс
Урок по алгебре Квадратные уравнения 8 класс Решение квадратных уравнений разными методами
Решение квадратных уравнений разными методами Координатная плоскость
Координатная плоскость Формулы сокращенного умножения
Формулы сокращенного умножения Презентация Десятичные дроби 5 класс
Презентация Десятичные дроби 5 класс Математическая выставка 6 класс
Математическая выставка 6 класс Внеклассное мероприятие по математике Кто хочет стать миллионером
Внеклассное мероприятие по математике Кто хочет стать миллионером Разность квадратов.
Разность квадратов. Уравнения n-ой степени
Уравнения n-ой степени урок- играделение обыкновенных дробей
урок- играделение обыкновенных дробей Заключительный урок в 5 классе
Заключительный урок в 5 классе Рациональные числа
Рациональные числа Презентация к уроку Умножение десятичных дробей на натуральные числа
Презентация к уроку Умножение десятичных дробей на натуральные числа Тригонометрия за...
Тригонометрия за... Презентация к уроку Одночлен и его стандартный вид
Презентация к уроку Одночлен и его стандартный вид Применение математических функций в физике
Применение математических функций в физике Турнир эрудитов
Турнир эрудитов Разработка урока по теме : Длина окружности
Разработка урока по теме : Длина окружности Математическая игра - Звёздный час
Математическая игра - Звёздный час Урок алгебры в 11 классе Решение логарифмических неравенств
Урок алгебры в 11 классе Решение логарифмических неравенств Построение индивидуальной образовательной траектории на уроках математики
Построение индивидуальной образовательной траектории на уроках математики Линейное уравнение с двумя переменными и его график
Линейное уравнение с двумя переменными и его график Сценарий и презентация внеклассного мероприятия по математике Юный математик
Сценарий и презентация внеклассного мероприятия по математике Юный математик Решение линейных неравенств.
Решение линейных неравенств. Сравнение дробей 5 класс
Сравнение дробей 5 класс МО математиков
МО математиков Презентация к уроку Формулы сокращенного умножения. Бином Ньютона
Презентация к уроку Формулы сокращенного умножения. Бином Ньютона