Содержание
- 2. ЦЕЛЬ: Систематизировать, обобщить, расширить знания и умения, связанные с применением методов решения тригонометрических уравнений
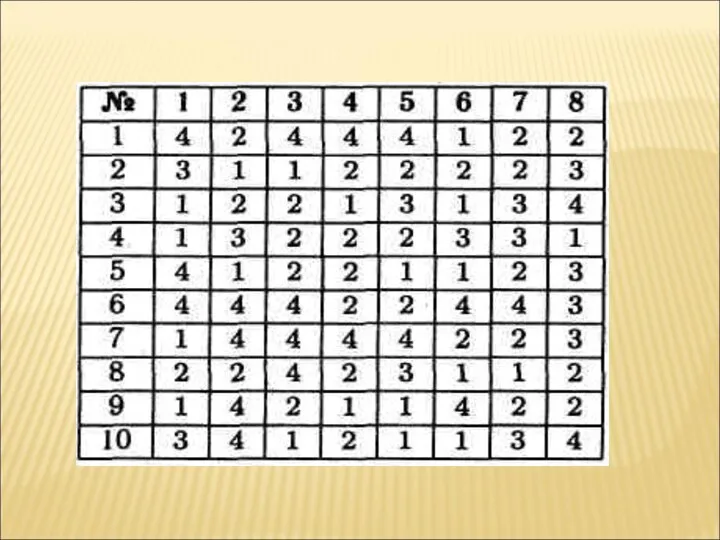
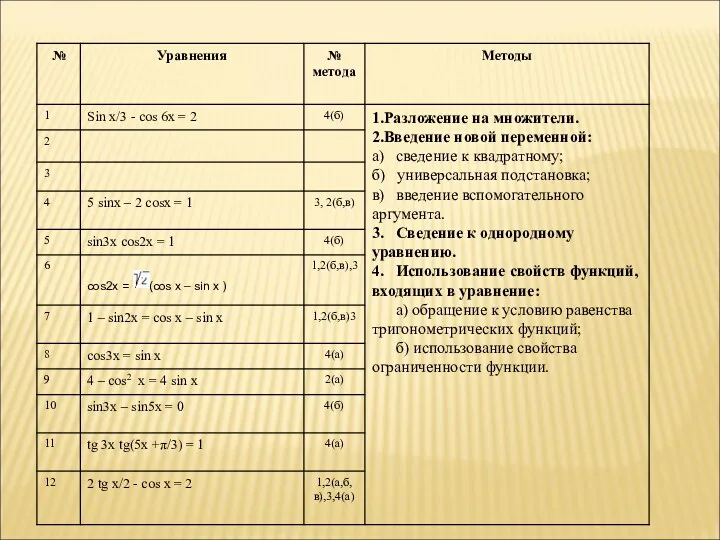
- 5. 1. Какие методы решения тригонометрических уравнений вы знаете? 2. Определите и ответьте, какими методами нужно решать
- 6. Некоторые типы тригонометрических уравнений. Уравнения, сводящиеся к квадратным, относительно cos х = t, sin х =
- 7. 4. Понижение степени. А cos2x + В = C. A cos2x + B = C. Решаются
- 8. Формулы. Универсальная подстановка. х ≠ π + 2πn; Проверка обязательна! Понижение степени. = (1 + cos2x
- 9. Сведение к однородному. Разложение на множители.
- 10. 1.Потеря корней: делим на g(х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2.
- 11. Уравнение . Уравнение . Поделив уравнение на , получим , , При решении этой задачи обе
- 12. , x = y + . Решить уравнение cos²x + sinx cosx = 0 1) Делить
- 13. Уравнения, линейные относительно sin x и cos x а sin x + в cos x =
- 14. Данное уравнение является уравнением вида , (1) где , , , которое можно решить другим способом.
- 15. Уравнение . Используя формулы sin x = 2 sin cos , cos x = cos2 -
- 16. РЕШИТЬ УРАВНЕНИЕ 4sin²x – 4sinx – 3 = 0 2cos²x – sinx – 1 = 0
- 17. ОТВЕТЫ. 4sin²x - 4 sinx – 3 = 0 ( -1)n+1 П/6 +Пn, n Z. 2
- 18. РЕШИТЬ УРАВНЕНИЕ
- 19. Решить уравнение Здесь Поделим обе части уравнения на 5: Введем вспомогательный аргумент , такой, что ,
- 23. Скачать презентацию

















 Сложение натуральных чисел и его свойства - презентация
Сложение натуральных чисел и его свойства - презентация Презентация к уроку алгебры в 10 классе Формулы приведения
Презентация к уроку алгебры в 10 классе Формулы приведения урок алгебы 7 класс по теме Квадрат суммы и квадрат разности двух выражений
урок алгебы 7 класс по теме Квадрат суммы и квадрат разности двух выражений Урок в 6 классе
Урок в 6 классе Математика 6 класс. Координатная плоскость Задания для развития и обучения учащихся (задания для интерактивной доски)
Математика 6 класс. Координатная плоскость Задания для развития и обучения учащихся (задания для интерактивной доски) презентация к уроку-исследования
презентация к уроку-исследования Презентации для урока математики по темеПрямая и обратная пропорциональность
Презентации для урока математики по темеПрямая и обратная пропорциональность Мультимедийный путеводитель Математический Петербург: опыт погружения математики в городскую среду
Мультимедийный путеводитель Математический Петербург: опыт погружения математики в городскую среду Материал для проведения Недели математики (Информация для стенда и задания)
Материал для проведения Недели математики (Информация для стенда и задания) Наибольшее и наименьшее значения функции
Наибольшее и наименьшее значения функции Законы арифметических действий
Законы арифметических действий Решение задач ЕГЭ: В8, В14
Решение задач ЕГЭ: В8, В14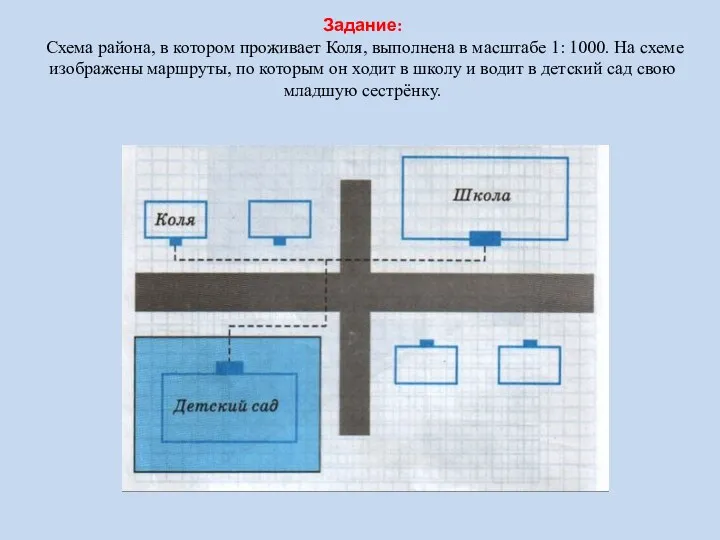 Расстояние между двумя точками. Масштаб.
Расстояние между двумя точками. Масштаб. Презентация к уроку математики в 5 кл:Геометрические тела. Объем прямоугольного параллелепипеда
Презентация к уроку математики в 5 кл:Геометрические тела. Объем прямоугольного параллелепипеда Деление с остатком
Деление с остатком Открытый урок в 6 классе. Геометрические тела
Открытый урок в 6 классе. Геометрические тела Решение системы линейных уравнений
Решение системы линейных уравнений Презентация по теме Правила вычисления производных
Презентация по теме Правила вычисления производных Проценты в современной жизни
Проценты в современной жизни кабинет математики
кабинет математики Три типа задач на проценты, 5 класс
Три типа задач на проценты, 5 класс Подготовка к ЕГЭ. Решение задач на смеси.
Подготовка к ЕГЭ. Решение задач на смеси. Презентация Ю.А. Гагарин к уроку математики в 5 классе
Презентация Ю.А. Гагарин к уроку математики в 5 классе Нахождение дроби от числа
Нахождение дроби от числа Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Презентация: Множества. Операции над множествами.
Презентация: Множества. Операции над множествами. 6 класс Математика Взаимно обратные числа. Урок1
6 класс Математика Взаимно обратные числа. Урок1 Тренажёр по теме Сложение и вычитание десятичных дробей, 5 класс
Тренажёр по теме Сложение и вычитание десятичных дробей, 5 класс