Содержание
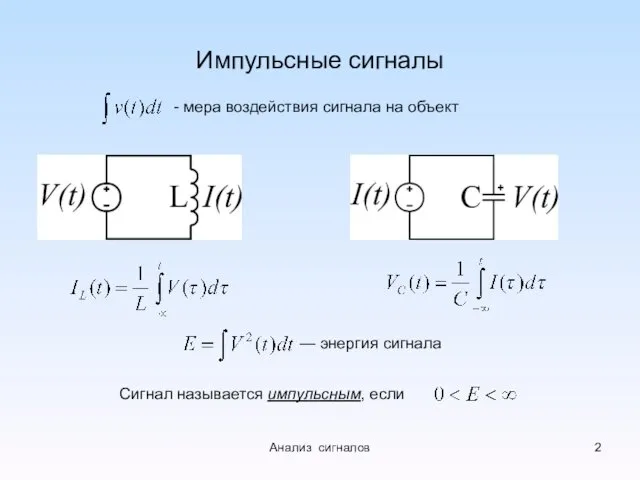
- 2. Импульсные сигналы - мера воздействия сигнала на объект — энергия сигнала Сигнал называется импульсным, если Анализ
- 3. Примеры импульсных сигналов — единичный импульс формально единичный импульс не является импульсным сигналом Анализ сигналов
- 4. Периодические сигналы Периодическим называется сигнал, повторяющийся через равные промежутки времени Наименьшая величина сигнала, удовлетворяющая этому определению
- 5. Случайные сигналы Случайный сигнал порождается случайным процессом Случайный сигнал часто называют выборочной функцией процесса Случайный дискретный
- 6. Если случайный сигнал принимает непрерывный ряд значений, то вместо вероятности pk пользуются плотностью вероятности P(v), которая
- 7. Стационарные случайные процессы Статистические характеристики сигнала, порожденного стационарным случайным процессом, не меняются с течением времени Выборочная
- 8. Рассмотрим случайный сигнал v, имеющий плотность вероятности P(v) Для такого сигнала отклонение от среднего равняется: Так
- 9. Вычислим среднюю мощность для важного частного случая — нормального (гауссова) распределения вероятности: Такое распределение имеет, например,
- 10. Четная и нечетные составляющие Сигнал можно разбить на четную и нечетные составляющие: — четная составляющая —
- 11. Действительная и мнимая составляющие Сигнал, мгновенное значение которого является комплексной величиной, описывается суммой действительной и мнимой
- 12. Сравнение сигналов Для того, чтобы ответить на вопрос, насколько два сигнала похожи, удобно воспользоваться аналогией с
- 13. Применительно к электрическим сигналам, для нахождения «проекции» сигнала v1(t) на сигнал v2(t) необходимо минимизировать среднюю мощность
- 14. Это выражение принимает минимум при: Анализ сигналов
- 15. Корреляционная функция Автокорреляционная функция (АКФ) импульсного сигнала: Взаимная корреляционная функция двух сигналов: — энергия сигнала —
- 16. в частности: АКФ является симметричной функцией; причем ее действительная часть является четной функцией, а мнимая —
- 17. — АКФ для сигналов конечной мощности — корреляционная функция для сигналов конечной мощности Анализ сигналов
- 18. Анализ сигналов
- 19. Свертка — свертка двух функций — коммутативность — ассоциативность — линейность Свойства свертки: Анализ сигналов
- 20. Для удобства введем обозначение: тогда: — АКФ корреляционной функции 2-х сигналов Автокорреляционная функция корреляционной функции 2-х
- 21. Тригонометрический ряд Фурье для периодических сигналов Разложение периодического сигнала в ряд Фурье — способ разложения сигнала
- 22. Величина n-ой гармоники определяется коэффициентом корреляции, называемыми коэффициентами ряда Фурье: — ряд Фурье Анализ сигналов
- 23. Анализ сигналов
- 24. Анализ сигналов
- 25. Экспоненциальный ряд Фурье Анализ сигналов
- 26. —мощность периодического сигнала Анализ сигналов
- 27. АКФ периодического сигнала, представленного в виде экспоненциального ряда: —ряд Фурье для АКФ сигнала, где Коэффициент Фn
- 28. Интеграл Фурье для импульсного сигнала — спектр сигнала Спектр импульсного сигнала непрерывен, причем составляющая на частоте
- 29. АКФ импульсного сигнала: — энергия импульсного сигнала Анализ сигналов
- 30. Представим сигнал v(t) через четную и нечетную составляющие и подставим в формулу для преобразования Фурье: Анализ
- 31. Связь ряда Фурье и преобразования Фурье Выберем из периодического сигнала k=2m+1 периодов: Анализ сигналов
- 32. Анализ сигналов
- 34. Скачать презентацию





























 Голография
Голография Радиографические методы
Радиографические методы Гидростатика. Поверхностные явления. Гидромеханика идеальной и вязкой жидкости. Практическое занятие 5
Гидростатика. Поверхностные явления. Гидромеханика идеальной и вязкой жидкости. Практическое занятие 5 Презентация по физике для 7 класса по теме Простые механизмы
Презентация по физике для 7 класса по теме Простые механизмы Отражение света
Отражение света Полимерные нанокомпозиты
Полимерные нанокомпозиты Принцип работы и техническая характеристика дыхательного аппарата на сжатом воздухе. Тема 3.1
Принцип работы и техническая характеристика дыхательного аппарата на сжатом воздухе. Тема 3.1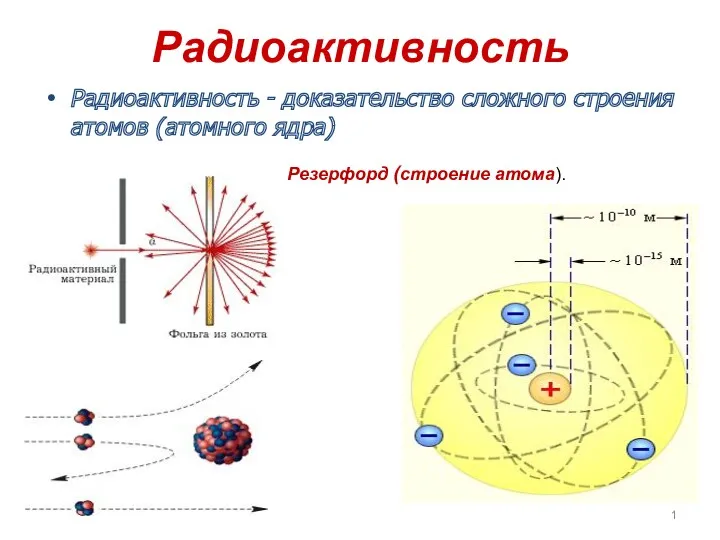 Радиоактивность, виды излучений, изотопы,распады
Радиоактивность, виды излучений, изотопы,распады Основні закони люмінесценції. (Тема 2)
Основні закони люмінесценції. (Тема 2) Световые явления. Распространение света
Световые явления. Распространение света Элементы игр на уроках физики
Элементы игр на уроках физики Проекционный аппарат
Проекционный аппарат Стоячие волны. Колебания и волны 14
Стоячие волны. Колебания и волны 14 Тест по физике (10 класс)
Тест по физике (10 класс) Законы Ньютона
Законы Ньютона Многоэлектронные атомы. Взаимодействие атомов с излучением
Многоэлектронные атомы. Взаимодействие атомов с излучением Двигатели внутреннего сгорания
Двигатели внутреннего сгорания Анализ и перспективы развития элегазового и вакуумного оборудования подстанций энергосистемы
Анализ и перспективы развития элегазового и вакуумного оборудования подстанций энергосистемы Введение в физику
Введение в физику Айнымалы ток генераторы
Айнымалы ток генераторы приемы целеполагания
приемы целеполагания Интегрированный урок (физика – экология) в 8 классе по теме: Тепловые двигатели и охрана окружающей среды
Интегрированный урок (физика – экология) в 8 классе по теме: Тепловые двигатели и охрана окружающей среды Презентация к уроку по физике посвящённая Дню космонавтики.
Презентация к уроку по физике посвящённая Дню космонавтики. Bell Ringer. What do you think of when you hear the word energy?
Bell Ringer. What do you think of when you hear the word energy? Прав ли был Прометей, давший людям огонь?
Прав ли был Прометей, давший людям огонь? Основные понятия и законы теории электромагнитного поля и теории электрических цепей
Основные понятия и законы теории электромагнитного поля и теории электрических цепей Значение радиоволн для физики и человечества. 11 класс
Значение радиоволн для физики и человечества. 11 класс Радиоактивность. Виды радиоактивных излучений
Радиоактивность. Виды радиоактивных излучений