Содержание
- 2. 1. Следствия из Т. об изменении момента количества движения 1) При движении под действием центральной силы
- 3. 2. Скорость точки Кинематика: радиальная компонента трансверсальная компонента Исключаем время используя закон площадей новая переменная
- 4. 3. Уравнение Бинэ Диф. уравнение траектории точки, движущейся под действием центральной силы (уравнение Бинэ). Интеграл энергии
- 5. 4. Пример: движение по окружности Найти закон центральной силы, под действием которой точка будет двигаться по
- 6. 5. Законы Кеплера 1) Все планеты (и кометы) описывают вокруг Солнца плоские орбиты, следуя закону площадей.
- 7. 6. Следствие из второго закона постоянная Гаусса 2-й закон сила, действующая на планеты, будет силой, притягивающей
- 8. 3ий з-н Ньютона 7. Следствие из третьего закона Солнце притягивает Землю с силой Земля притягивает Солнце
- 9. Траекторией точки будет коническое сечение (эллипс, парабола или гипербола), один из фокусов которого совпадает с притягивающим
- 10. 9. Виды траекторий Пусть в точке Р (перицентр) известна скорость . Каков будет вид траектории? параболическая
- 11. 10. Виды траекторий и энергия Выразим эксцентриситет через постоянную энергии Нормированный на m интеграл энергии полная
- 12. 11. Определение параметров траектории по начальным данным Известны Найти 1) Найти константы площадей и энергии 2)
- 13. 12. Движение вдоль орбиты. Уравнение Кеплера Закон площадей Замена переменных эксцентрическая аномалия
- 15. Скачать презентацию












 Семинарское занятие по теме основы электростатики, 10 класс
Семинарское занятие по теме основы электростатики, 10 класс Баяндама Альберт Эйнштейн
Баяндама Альберт Эйнштейн Основные уравнения электростатики в вакууме. (Лекция 2)
Основные уравнения электростатики в вакууме. (Лекция 2) Квантовые свойства электромагнитного излучения. Фотоэффект
Квантовые свойства электромагнитного излучения. Фотоэффект Изучение треков заряженных частиц по готовым фотографиям
Изучение треков заряженных частиц по готовым фотографиям Моторамы. Назначение моторам
Моторамы. Назначение моторам Выбор передаточных чисел узлов трансмиссии. Общее число передач или ступеней трансмиссии. Лекция 14
Выбор передаточных чисел узлов трансмиссии. Общее число передач или ступеней трансмиссии. Лекция 14 Измерение атмосферного давления. 7 класс
Измерение атмосферного давления. 7 класс Элементы квантовой теории (продолжение). Лекция 10
Элементы квантовой теории (продолжение). Лекция 10 Курс лекций по сопротивлению материалов (модуль 2, лекции 9-17)
Курс лекций по сопротивлению материалов (модуль 2, лекции 9-17) Физика в картинках
Физика в картинках Предметная неделя
Предметная неделя Активізація пізнавальної діяльності учнів на уроках фізики шляхом використання проблемних ситуацій
Активізація пізнавальної діяльності учнів на уроках фізики шляхом використання проблемних ситуацій Урок физики в 9 классе Магнитное поле. Линии магнитного поля
Урок физики в 9 классе Магнитное поле. Линии магнитного поля Общее устройство автомобиля
Общее устройство автомобиля Тепловое загрязнение
Тепловое загрязнение Расчет сложных электрических цепей постоянного тока
Расчет сложных электрических цепей постоянного тока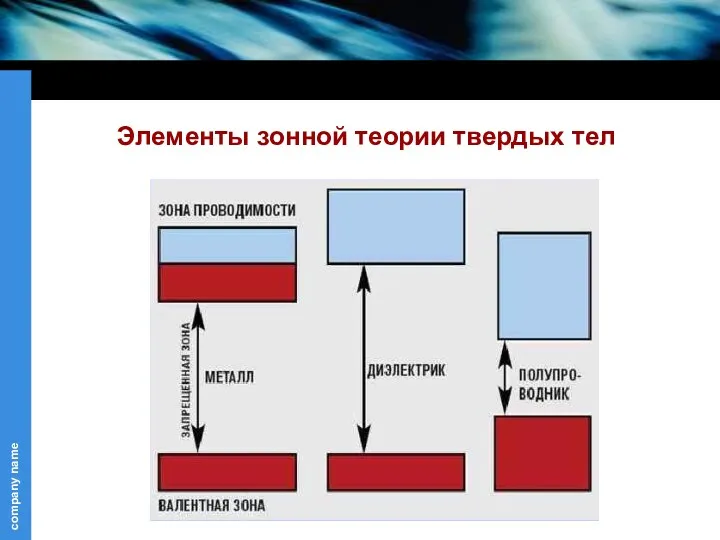 Зонная теория твердых тел
Зонная теория твердых тел Метод вузлових напруг
Метод вузлових напруг Жидкостные термометры
Жидкостные термометры Активизация познавательной деятельности учащихся при изучении физики
Активизация познавательной деятельности учащихся при изучении физики Давление. От чего зависит результат действия силы?
Давление. От чего зависит результат действия силы? Использование технологии развития критического мышления на уроках математики и физики
Использование технологии развития критического мышления на уроках математики и физики Стационарная теплопроводность. (Лекции 6-7)
Стационарная теплопроводность. (Лекции 6-7) Экспериментальные методы исследования частиц
Экспериментальные методы исследования частиц Путь к звездам
Путь к звездам Колебательный контур
Колебательный контур Как можно обрабатывать заготовки из древесины, имеющие цилиндрическую форму. Устройство токарного станка по дереву
Как можно обрабатывать заготовки из древесины, имеющие цилиндрическую форму. Устройство токарного станка по дереву