Содержание
- 2. х 1. Понятие о волновой функции Экспериментальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового дуализма привели
- 3. х Необходимость вероятностного подхода к описанию микрочастиц, является важнейшей отличительной особенностью квантовой теории.
- 4. х немецкий физик М. Борн в 1926 г. предположил, что по волновому закону меняется не сама
- 5. х описание микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат
- 6. х Вероятность нахождения частицы в объеме V равна:
- 7. х где данный интеграл вычисляется по всему бесконечному пространству, т.е. по координатам x, y, z от
- 8. Условие нормировкиволновой функции:
- 9. Чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна удовлетворять ряду ограничительных условий. конечной (вероятность
- 10. х Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями
- 11. х Волновая функция Ψ является основной характеристикой состояния микрообъектов.
- 12. х 2. Уравнение Шредингера Толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу, что
- 13. х Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э.Шредингером.
- 14. х Уравнение Шредингера в общем виде записывается так: где - постоянная Планка, m – масса частицы.
- 15. х Если силовое поле, в котором движется частица потенциально, то функция U не зависит явно от
- 16. Уравнение Шредингера для стационарных состояний
- 17. х Уравнение Шредингера для стационарных состояний можно переписать в виде: – оператор Гамильтона, равный сумме операторов
- 18. 3. Движение свободной частицы х Свободная частица – частица, движущаяся в отсутствие внешних полей. уравнение Шредингера
- 19. Проведем качественный анализ решений уравнения Шредингера, применительно к частице в яме с бесконечно высокими «стенками». 4.
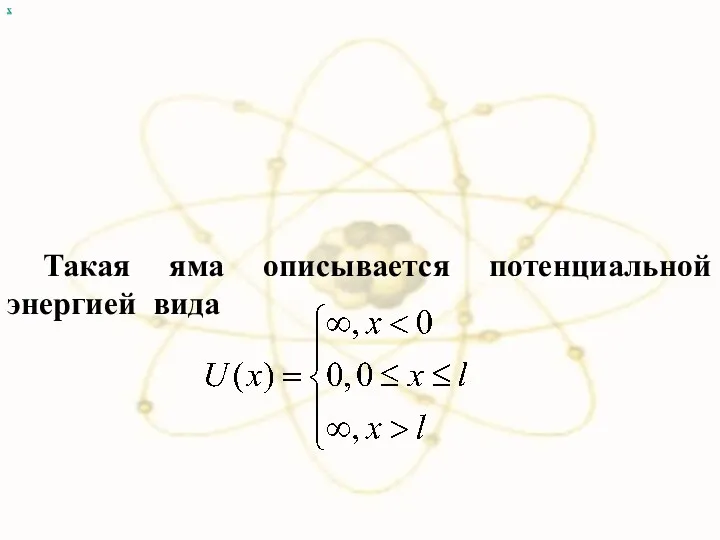
- 20. х Такая яма описывается потенциальной энергией вида
- 21. х По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее
- 22. х В пределах «ямы» (0 ≤ x ≤ l) уравнение Шредингера (5) сведется к уравнению (7)
- 23. х Отсюда следует, что: (11) где n = 1, 2, 3…
- 24. х Квантовые значения энергии En называется уровнями энергии, а число п, определяющее энергетические уровни - главным
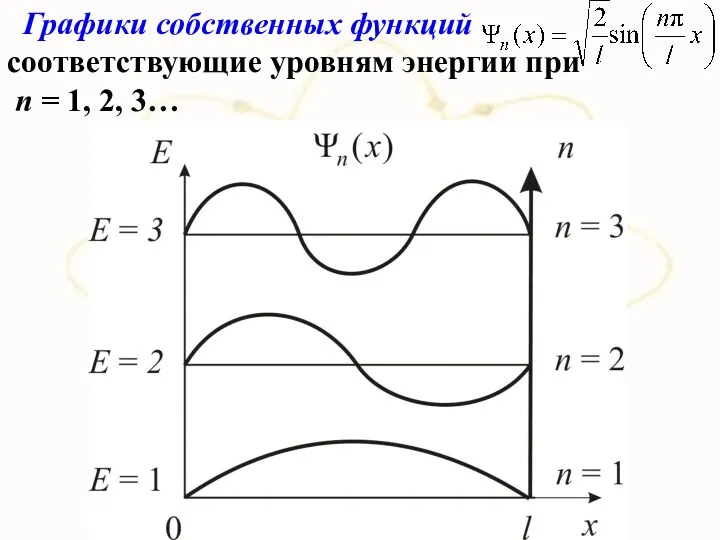
- 25. х Собственные функции будут иметь вид: где n = 1, 2, 3…
- 26. Графики собственных функций соответствующие уровням энергии при п = 1, 2, 3…
- 27. х В квантовом состоянии с п = 2 частица не может находиться в центре ямы, в
- 28. х Из выражения следует, что энергетический интервал между двумя соседними условиями равен
- 29. х Неопределенность координаты Δx частицы в яме шириной l равна Δx = l. Тогда согласно соотношению
- 30. при бoльших квантовых числах n>>1 х т.е. соседние уровни расположены тесно: тем теснее, чем больше п.
- 31. х Принцип соответствия: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а
- 32. х 5. Прохождение частиц сквозь потенциальный барьер. Туннельный эффект Рисунок 5 При данных условиях задачи классическая
- 33. х Уравнение Шредингера для состояний в каждой из выделенных областей имеет вид: Общее решение этих дифф.
- 34. , квантовая механика приводит к принципиально новому квантовому явлению - туннельному эффекту, в результате которого микрообъект
- 35. х Коэффициент прозрачности для барьера прямоугольной формы Для барьера произвольной формы
- 36. х Прохождение частицы сквозь ,барьер можно пояснить соотношением неопределенностей: Неопределенность импульса на отрезке Δx = l
- 37. С классической точки зрения прохождение частицы сквозь потенциальный барьер при E Туннельный эффект является специфическим квантовым
- 39. Скачать презентацию






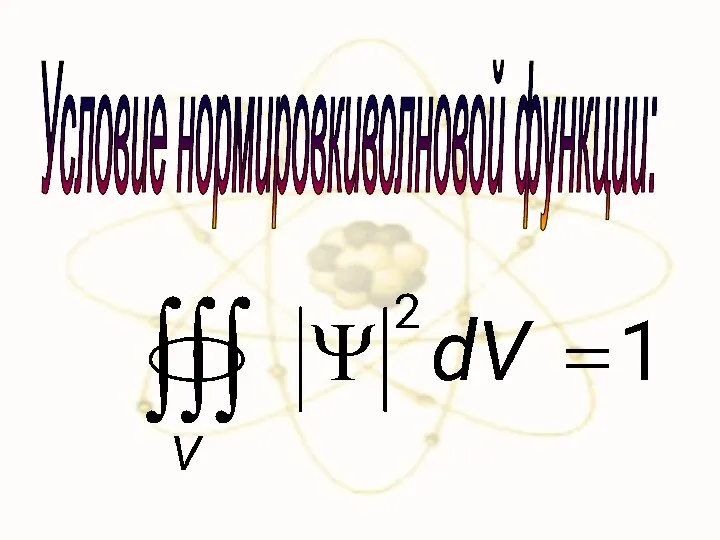


























 Интерференция света. (Лекция 11)
Интерференция света. (Лекция 11) Происхождение элементов
Происхождение элементов Кроссворд
Кроссворд Молекулярно-кинетическая теория строения вещества (МКТ)
Молекулярно-кинетическая теория строения вещества (МКТ) Кинематика тела. Лекция 7
Кинематика тела. Лекция 7 тест по состояниям вещества 8 класс
тест по состояниям вещества 8 класс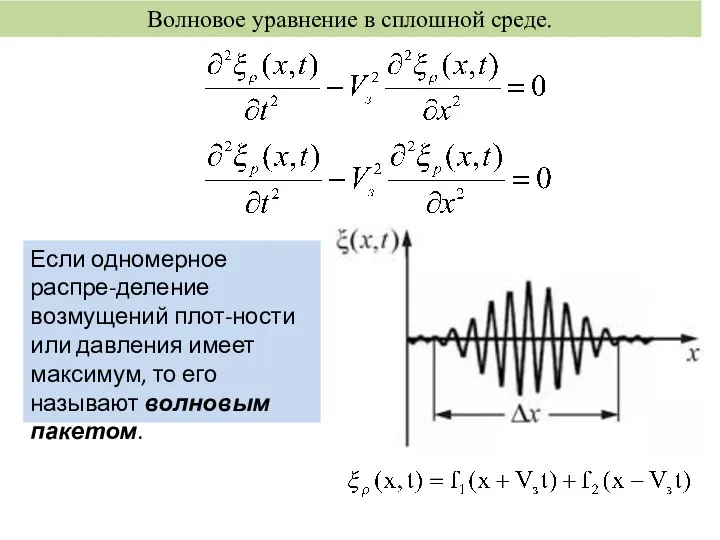 Волновое уравнение в сплошной среде
Волновое уравнение в сплошной среде Электромагнитные волны
Электромагнитные волны Методы исследования наносистем и наноматериалов. Классификация физико-химических методов исследования
Методы исследования наносистем и наноматериалов. Классификация физико-химических методов исследования Презентация к уроку физики в 8 классе: Обобщение по теме Агрегатные состояния вещества.
Презентация к уроку физики в 8 классе: Обобщение по теме Агрегатные состояния вещества. Магнитные материалы. Магнитное поле в веществе
Магнитные материалы. Магнитное поле в веществе Урок физики 8 класс Испарение и конденсация
Урок физики 8 класс Испарение и конденсация Аеродинамічні характеристики літака. Аеродинамічне компонування літака. (Лекція 7.4.1)
Аеродинамічні характеристики літака. Аеродинамічне компонування літака. (Лекція 7.4.1) 03.21г. Типы спектров. Спектральный анализ
03.21г. Типы спектров. Спектральный анализ Фундаментальные взаимодействия
Фундаментальные взаимодействия Презентация к уроку Водород, 5 класс, предмет Физика и химия
Презентация к уроку Водород, 5 класс, предмет Физика и химия Закон Гука
Закон Гука Лабораторная работа №2. Измерение массы тела на рычажных весах
Лабораторная работа №2. Измерение массы тела на рычажных весах Электризация тел. Два рода зарядов
Электризация тел. Два рода зарядов Поляризация поперечных волн. Поляризация света. Дисперсия света. Виды спектров
Поляризация поперечных волн. Поляризация света. Дисперсия света. Виды спектров Батарейка своими руками
Батарейка своими руками Качество электроэнергии
Качество электроэнергии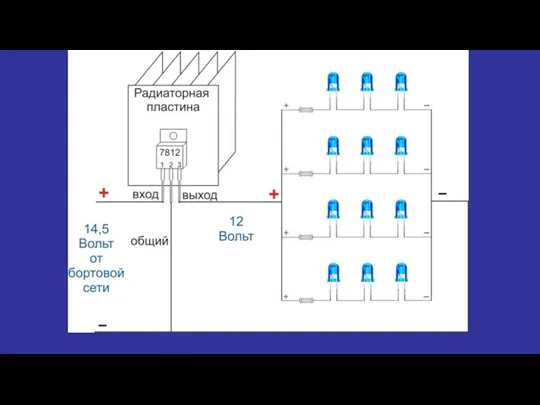 Электрическая схема светильника с регулировкой мощности
Электрическая схема светильника с регулировкой мощности Шлифовальные станки. (Тема 7)
Шлифовальные станки. (Тема 7) Электромагнитная картина мира
Электромагнитная картина мира Курсовая работа по теоретической механике “Динамика кулисного механизма”
Курсовая работа по теоретической механике “Динамика кулисного механизма”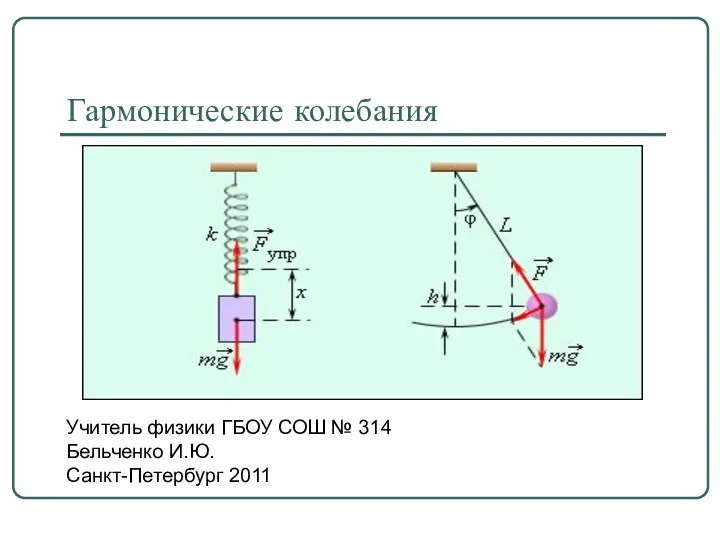 Гармонические колебания
Гармонические колебания Работа силы Ампера. Магнитный поток. Явление электромагнитной индукции. Закон электромагнитной индукции. Правило Ленца
Работа силы Ампера. Магнитный поток. Явление электромагнитной индукции. Закон электромагнитной индукции. Правило Ленца