Содержание
- 2. Learning objective Be able to find the kinematic quantities (position, displacement, velocity, and acceleration) of a
- 3. Applications The motion of large objects, such as rockets, airplanes, or cars, can often be analyzed
- 4. Applications A sports car travels along a straight road. Can we treat the car as a
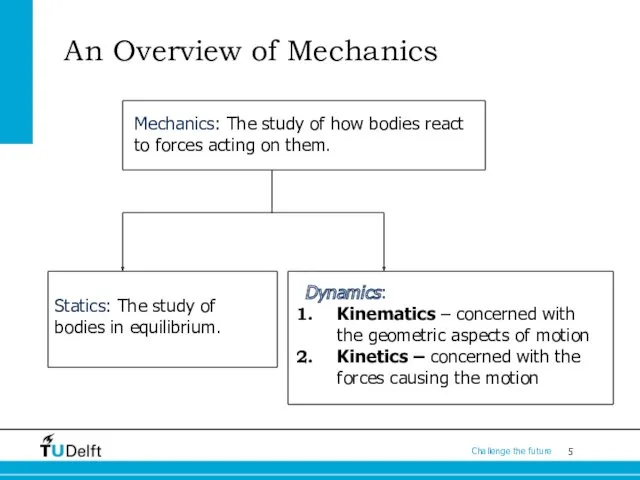
- 5. An Overview of Mechanics
- 6. Chapter 12: Kinematics of a Particle Section 12.2: Rectilinear Kinematics: Continuous Motion
- 7. Continuous Motion A particle travels along a straight-line path defined by the coordinate axis s. The
- 8. Velocity Velocity is a measure of the rate of change in the position of a particle.
- 9. Acceleration Acceleration is the rate of change in the velocity of a particle. It is a
- 10. Summary of Kinematic Relations • Differentiate position to get velocity and acceleration. v = ds/dt ;
- 11. Constant Acceleration The three kinematic equations can be integrated for the special case when acceleration is
- 12. Example Plan: Establish the positive coordinate, s, in the direction the particle is traveling. Since the
- 13. Solution 1) Take a derivative of the velocity to determine the acceleration. a = dv /
- 14. Channel Setting Instructions for ResponseCard RF 1. Press and release the "GO" or "CH" button. 2.
- 15. Quiz
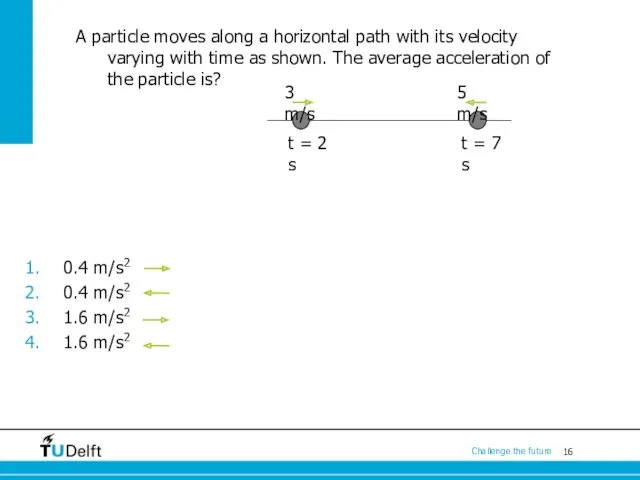
- 16. A particle moves along a horizontal path with its velocity varying with time as shown. The
- 17. A particle has an initial velocity of 30 m/s to the left. If it then passes
- 18. Example Given: A particle is moving along a straight line such that its velocity is defined
- 19. Solution
- 20. Solution 2) Take a derivative of distance to calculate the velocity and acceleration.
- 21. Quiz
- 22. A particle has an initial velocity of 3 m/s to the left at s0 = 0
- 23. A particle is moving with an initial velocity of v = 12 m/s and constant acceleration
- 24. Ugly aircraft competition
- 25. Scale of Ugliness 1 = most beautiful aircraft ever built 2 = extremely beautiful aircraft 3
- 26. Focke Wulf 19a Ente (1927) 1 2 3 4 5 6 7 8 9 10
- 27. Chapter 12: Kinematics of a Particle Section 12.3: Rectilinear Kinematics: Erratic Motion
- 28. Learning Objective Be able to calculate position, velocity, and acceleration of a particle using graphs.
- 29. Erratic Motion The approach builds on the facts that slope and differentiation are linked and that
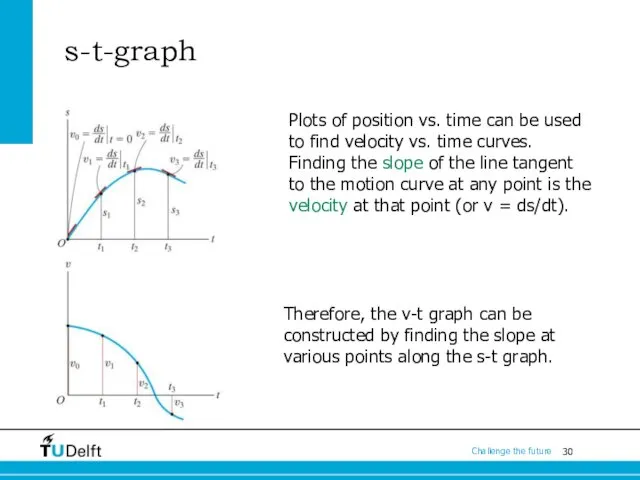
- 30. s-t-graph
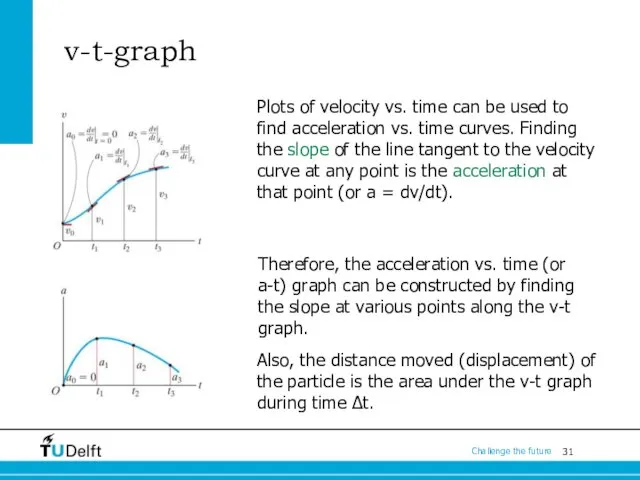
- 31. v-t-graph Also, the distance moved (displacement) of the particle is the area under the v-t graph
- 32. a-t-graph
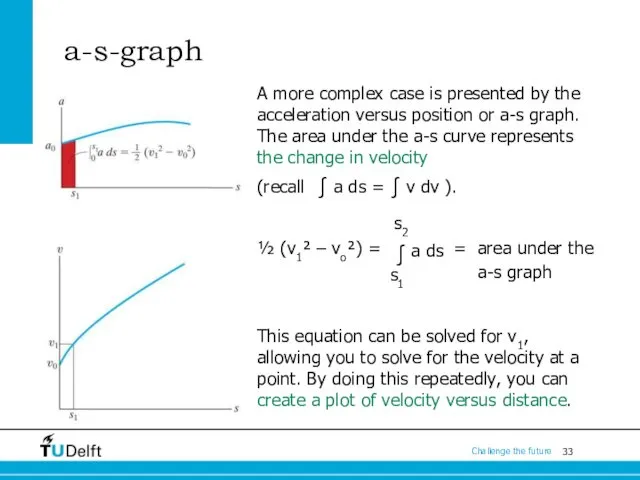
- 33. a-s-graph
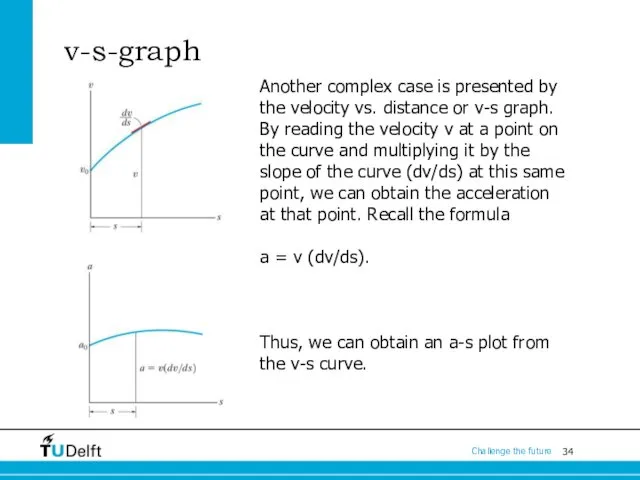
- 34. v-s-graph Another complex case is presented by the velocity vs. distance or v-s graph. By reading
- 35. Example What is your plan of attack for the problem?
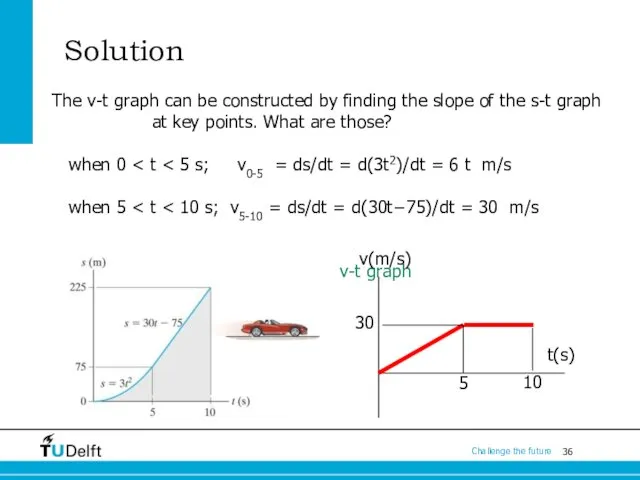
- 36. Solution The v-t graph can be constructed by finding the slope of the s-t graph at
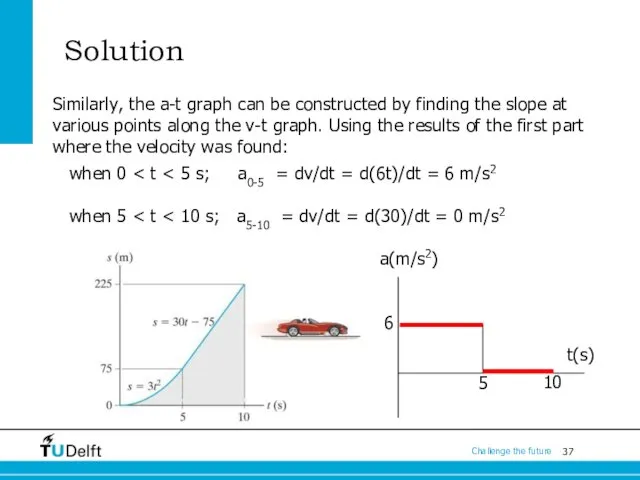
- 37. Solution Similarly, the a-t graph can be constructed by finding the slope at various points along
- 38. Quiz
- 39. If a particle starts from rest and accelerates according to the graph shown, the particle’s velocity
- 40. The particle in the previous stops moving at t = ……. 10 s 20 s 30
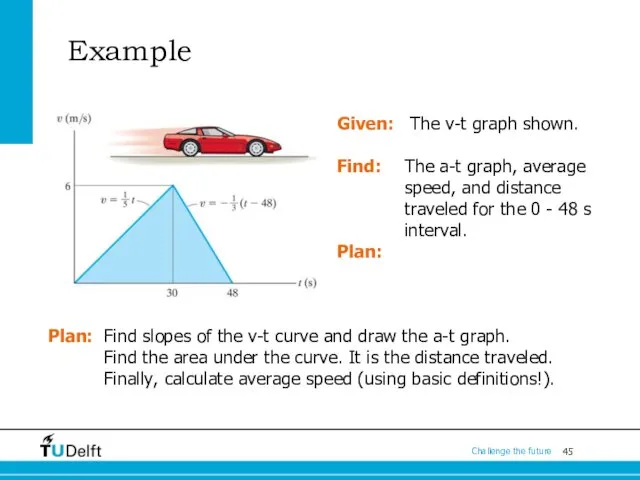
- 41. Example Given: The v-t graph shown. Find: The a-t graph, average speed, and distance traveled for
- 42. Example Given: The v-t graph shown. Find: The a-t graph, average speed, and distance traveled for
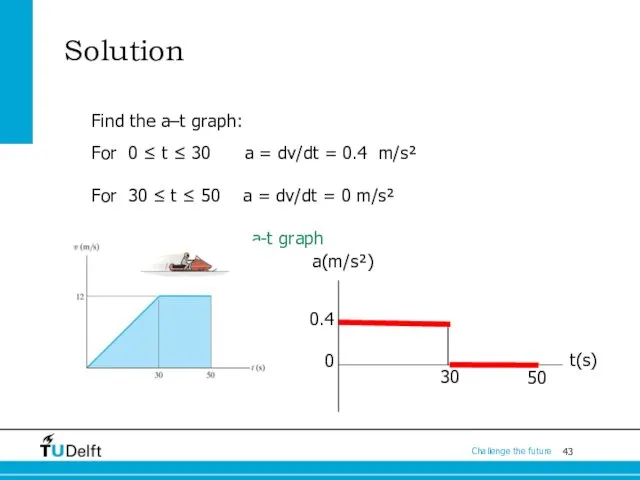
- 43. Solution Find the a–t graph: For 0 ≤ t ≤ 30 a = dv/dt = 0.4
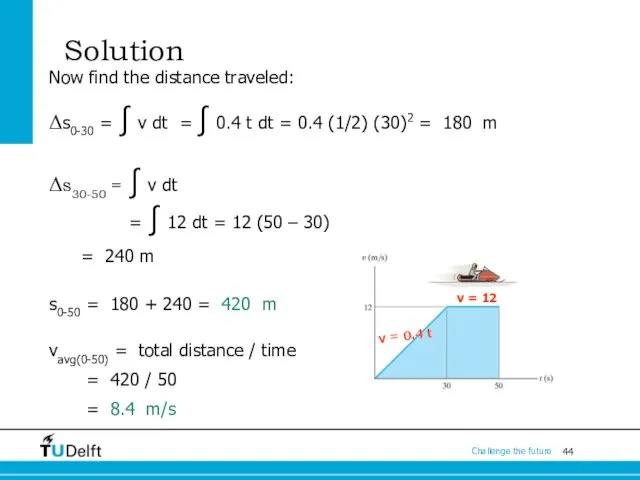
- 44. Solution Now find the distance traveled: Δs0-30 = ∫ v dt = ∫ 0.4 t dt
- 45. Example Given: The v-t graph shown. Find: The a-t graph, average speed, and distance traveled for
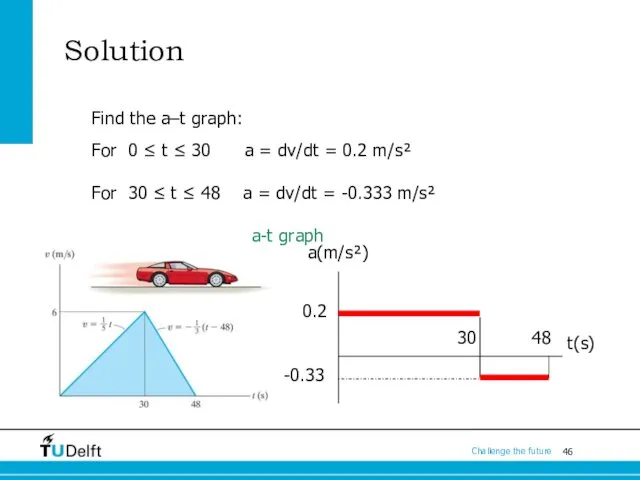
- 46. Solution Find the a–t graph: For 0 ≤ t ≤ 30 a = dv/dt = 0.2
- 47. Solution Now find the distance traveled: Δs0-30 = ∫ v dt = (1/5)(1/2) (30)2 = 90
- 48. Example Given: An aircraft is accelerating whilst taxiing. It starts with a speed of 2 m/s.
- 49. Solution
- 50. Quiz
- 51. If a car has the velocity curve shown, determine the time t necessary for the car
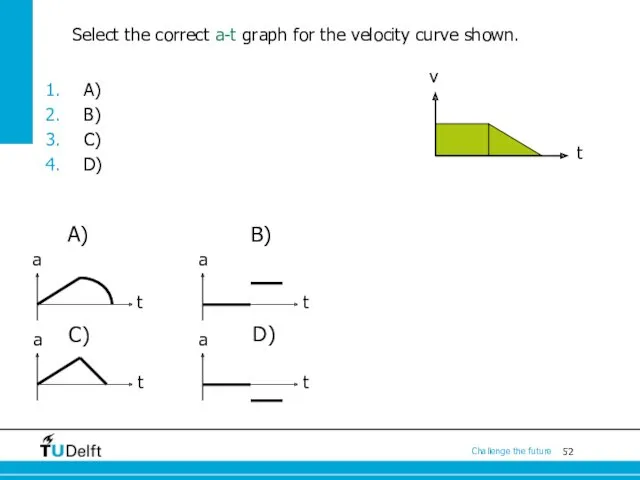
- 52. Select the correct a-t graph for the velocity curve shown. a t a t a t
- 53. Ugly aircraft competition
- 54. Miles M.35 Libellula (1942) 1 2 3 4 5 6 7 8 9 10
- 55. Chapter 12: Kinematics of a Particle Section 12.4: General Curvilinear Motion
- 56. Learning Objective Be able to describe the motion of a particle traveling along a curved path.
- 57. Applications The path of motion of a plane can be tracked with radar and its x,
- 58. Applications A roller coaster car travels down a fixed, helical path at a constant speed.
- 59. General Curvilinear Motion A particle moving along a curved path undergoes curvilinear motion. Since the motion
- 60. Velocity Velocity represents the rate of change in the position of a particle. The average velocity
- 61. Acceleration Acceleration represents the rate of change in the velocity of a particle. If a particle’s
- 62. Chapter 12: Kinematics of a Particle Section 12.5: Curvilinear Motion Rectangular Components
- 63. Learning Objective Be able to relate kinematic quantities in terms of the rectangular components of the
- 64. Rectangular Components It is often convenient to describe the motion of a particle in terms of
- 65. Rectangular Components: Velocity
- 66. Rectangular Components: Acceleration The direction of a is usually not tangent to the path of the
- 67. Example Given:The box slides down the slope described by the equation y = (0.05 x2) m,
- 68. Solution
- 69. Solution
- 70. Quiz
- 71. If the position of a particle is defined by r = [(1.5t2 + 1) i +
- 72. The position of a particle is given as r = (4t2 i - 2x j) m.
- 73. Ugly aircraft competition
- 74. Kyushu J7W-1 Shinden (1945) 1 2 3 4 5 6 7 8 9 10
- 75. Chapter 12: Kinematics of a Particle Section 12.6: Motion of a Projectile
- 76. Learning Objective Be able to analyze the free-flight motion of a projectile.
- 77. Applications A firefighter needs to know the maximum height on the wall she can project water
- 78. Motion of a Projectile Projectile motion can be treated as two rectilinear motions, one in the
- 79. Motion of a Projectile
- 80. Kinematic Equations: Horizontal Motion Since ax = 0, the velocity in the horizontal direction remains constant
- 81. Kinematic Equations: Vertical Motion Since the positive y-axis is directed upward, ay = – g. Application
- 82. Example Given: vA and θ Find: Horizontal distance it travels and vC. Plan: Apply the kinematic
- 83. Solution Horizontal distance the ball travels is; x = (10 cos 30) t x = (10
- 84. Example Plan: Establish a fixed x,y coordinate system (in this solution, the origin of the coordinate
- 85. Solution vA = 19.42 m/s
- 86. Quiz
- 87. The time of flight of a projectile, fired over level ground, with initial velocity Vo at
- 88. Ugly aircraft competition
- 89. VariViggen (1967) 1 2 3 4 5 6 7 8 9 10
- 90. Chapter 12: Kinematics of a Particle Section 12.7: Curvilinear Motion Normal and Tangential Components
- 91. Learning Objective Be able to calculate the normal and tangential components of velocity and acceleration of
- 92. Application A roller coaster travels down a hill for which the path can be approximated by
- 93. Normal and Tangential Components When a particle moves along a curved path, it is sometimes convenient
- 94. Normal and Tangential Components The position of the particle at any instant is defined by the
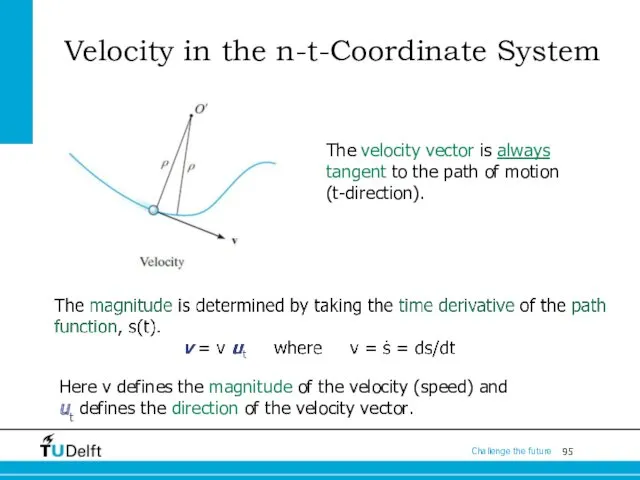
- 95. Velocity in the n-t-Coordinate System The velocity vector is always tangent to the path of motion
- 96. Velocity in the n-t-Coordinate System
- 97. Velocity in the n-t-Coordinate System So, there are two components to the acceleration vector: a =
- 98. Special Cases of Motion There are four special cases of motion to consider.
- 99. Special Cases of Motion 3) The tangential component of acceleration is constant, at = (at)c. In
- 100. Three-dimensional Motion If a particle moves along a space curve, the n and t axes are
- 101. Example Given: A car travels along the road with a speed of v = (2s) m/s,
- 102. Solution The velocity vector is v = v ut , where the magnitude is given by
- 103. Example Given: A boat travels around a circular path, r = 40 m, at a speed
- 104. Solution The velocity vector is v = v ut , where the magnitude is given by
- 105. Quiz
- 106. An aircraft traveling in a circular path of radius 300 m has an instantaneous velocity of
- 107. Example Given: The train engine at E has a speed of 20 m/s and an acceleration
- 108. Solution Acceleration Tangential component : at =14 cos(75) = 3.623 m/s2 Normal component : an =
- 109. Chapter 12: Kinematics of a Particle Section 12.8: Curvilinear Motion Cylindrical Components
- 110. Learning Objective Be able to calculate velocity and acceleration components using cylindrical coordinates.
- 111. Applications A cylindrical coordinate system is used in cases where the particle moves along a 3-D
- 112. Cylindrical Components We can express the location of P in polar coordinates as r = r
- 113. Velocity in Polar Coordinates
- 114. Acceleration in Polar Coordinates
- 115. Cylindrical Coordinates If the particle P moves along a space curve, its position can be written
- 116. Example Use the polar coordinate system. Given: The platform is rotating such that, at any instant,
- 117. Solution
- 118. Solution
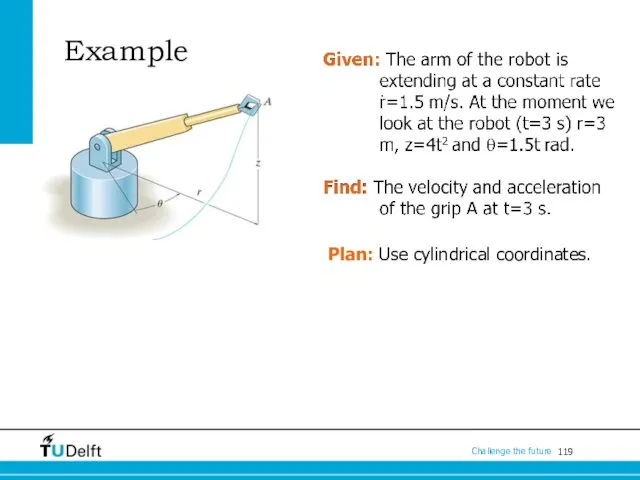
- 119. Example Plan: Use cylindrical coordinates.
- 120. Solution
- 121. Solution Acceleration equation in cylindrical coordinates
- 122. Ugly aircraft competition
- 123. Curtis Aerodrome (1914) 1 2 3 4 5 6 7 8 9 10
- 124. Chapter 12: Kinematics of a Particle Section 12.9: Absolute Dependent Motion of Two Particles
- 125. Learning Objective Be able to relate the positions, velocities, and accelerations of particles undergoing dependent motion.
- 126. Applications Rope and pulley arrangements are often used to assist in lifting heavy objects. The total
- 127. Applicatons The cable and pulley system shown can be used to modify the speed of the
- 128. Dependent Motion In many kinematics problems, the motion of one object will depend on the motion
- 129. Dependent Motion In this example, position coordinates sA and sB can be defined from fixed datum
- 130. Dependent Motion The negative sign indicates that as A moves down the incline (positive sA direction),
- 131. Example Consider a more complicated example. Position coordinates (sA and sB) are defined from fixed datum
- 132. Solution The position coordinates are related by the equation 2sB + h + sA = lT
- 133. Solution This example can also be worked by defining the position coordinate for B (sB) from
- 134. Dependent Motion: Procedure These procedures can be used to relate the dependent motion of particles moving
- 135. Example Given: In the figure on the left, the cord at A is pulled down with
- 136. Solution Define the datum line through the top pulley (which has a fixed position). sA can
- 137. Solution 3) Eliminating sC between the two equations, we get: sA + 4sB = l1 +
- 138. Quiz
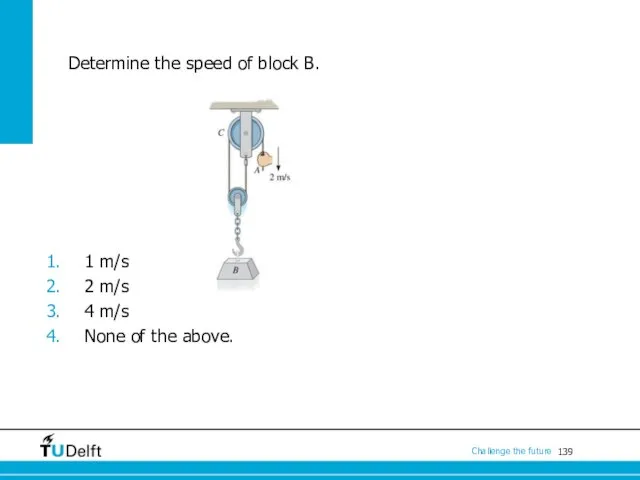
- 139. Determine the speed of block B. 1 m/s 2 m/s 4 m/s None of the above.
- 140. Example Given: In this pulley system, block A is moving downward with a speed of 4
- 141. Solution 2) Defining sA, sB, and sC as shown, the position relation can be written: sA
- 142. Quiz
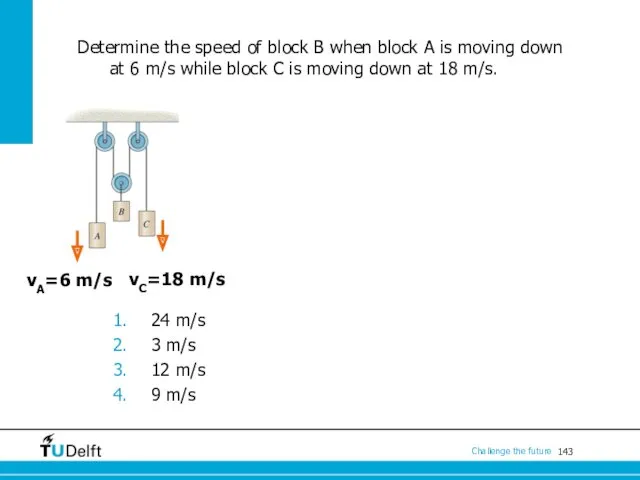
- 143. Determine the speed of block B when block A is moving down at 6 m/s while
- 144. Ugly aircraft competition
- 145. Koechlin biplane (1908) 1 2 3 4 5 6 7 8 9 10
- 146. Chapter 12: Kinematics of a Particle Section 12.10: Relative Motion of Two Particles Using Translating Axes
- 147. Learning Objective Be able to relate the positions, velocities, and accelerations of particles undergoing relative motion.
- 148. Applications A fighter aircraft is trying to intercept an airliner because communication got lost. The fighter
- 149. Relative Motion: Position Particles A and B are moving both along their own path. Their absolute
- 150. Relative Motion: Velocity and Acceleration For the velocity one can write: vB = vA + vB/A
- 151. Relative Motion: Procedure 3. These unknowns can be solved for either graphically or numerically using trigonometry
- 152. Example Given: Two boats are leaving the pier at the same moment but with different speeds
- 153. vA = 15 cos 30° i + 15 sin 30° j vB = 10 cos 60°
- 154. Quiz
- 155. Two planes A and B are flying at constant speed. Determine the magnitude of the velocity
- 156. Example Given: Aircraft A is flying along in a straight line, whereas fighter B is flying
- 157. Solution 1) For the velocity one can write: vB = vA + vB/A 600 j km/h
- 159. Скачать презентацию











































































































































 Семинарское занятие по теме основы электростатики, 10 класс
Семинарское занятие по теме основы электростатики, 10 класс Баяндама Альберт Эйнштейн
Баяндама Альберт Эйнштейн Основные уравнения электростатики в вакууме. (Лекция 2)
Основные уравнения электростатики в вакууме. (Лекция 2) Квантовые свойства электромагнитного излучения. Фотоэффект
Квантовые свойства электромагнитного излучения. Фотоэффект Изучение треков заряженных частиц по готовым фотографиям
Изучение треков заряженных частиц по готовым фотографиям Моторамы. Назначение моторам
Моторамы. Назначение моторам Выбор передаточных чисел узлов трансмиссии. Общее число передач или ступеней трансмиссии. Лекция 14
Выбор передаточных чисел узлов трансмиссии. Общее число передач или ступеней трансмиссии. Лекция 14 Измерение атмосферного давления. 7 класс
Измерение атмосферного давления. 7 класс Элементы квантовой теории (продолжение). Лекция 10
Элементы квантовой теории (продолжение). Лекция 10 Курс лекций по сопротивлению материалов (модуль 2, лекции 9-17)
Курс лекций по сопротивлению материалов (модуль 2, лекции 9-17) Физика в картинках
Физика в картинках Предметная неделя
Предметная неделя Активізація пізнавальної діяльності учнів на уроках фізики шляхом використання проблемних ситуацій
Активізація пізнавальної діяльності учнів на уроках фізики шляхом використання проблемних ситуацій Урок физики в 9 классе Магнитное поле. Линии магнитного поля
Урок физики в 9 классе Магнитное поле. Линии магнитного поля Общее устройство автомобиля
Общее устройство автомобиля Тепловое загрязнение
Тепловое загрязнение Расчет сложных электрических цепей постоянного тока
Расчет сложных электрических цепей постоянного тока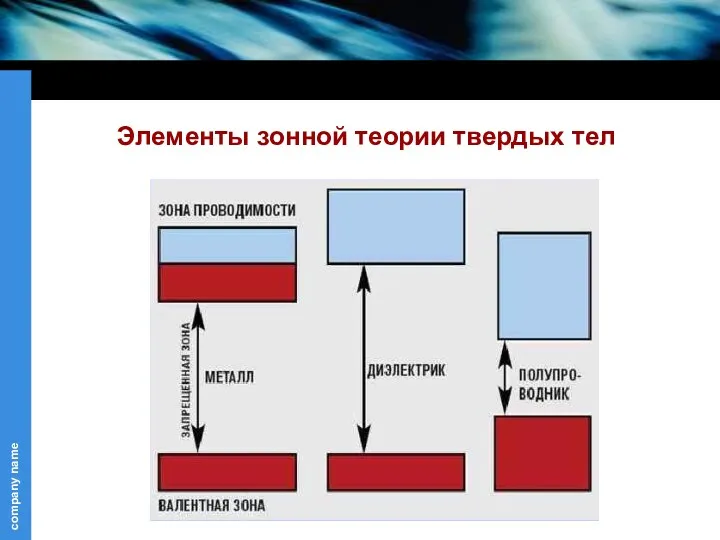 Зонная теория твердых тел
Зонная теория твердых тел Метод вузлових напруг
Метод вузлових напруг Жидкостные термометры
Жидкостные термометры Активизация познавательной деятельности учащихся при изучении физики
Активизация познавательной деятельности учащихся при изучении физики Давление. От чего зависит результат действия силы?
Давление. От чего зависит результат действия силы? Использование технологии развития критического мышления на уроках математики и физики
Использование технологии развития критического мышления на уроках математики и физики Стационарная теплопроводность. (Лекции 6-7)
Стационарная теплопроводность. (Лекции 6-7) Экспериментальные методы исследования частиц
Экспериментальные методы исследования частиц Путь к звездам
Путь к звездам Колебательный контур
Колебательный контур Как можно обрабатывать заготовки из древесины, имеющие цилиндрическую форму. Устройство токарного станка по дереву
Как можно обрабатывать заготовки из древесины, имеющие цилиндрическую форму. Устройство токарного станка по дереву