Содержание
- 2. Вопрос №1. Линейная модель бокового движения в векторно-матричной форме.
- 3. К изолированному боковому движению относится движение центра масс вдоль траекторной оси OZк, лежащей в горизонтальной плоскости,
- 4. Уравнения динамики бокового движения: Кинематические уравнения: Окончательный вид системы уравнений изолированного бокового движения :
- 5. Физический смысл коэффициентов, входящих в уравнение бокового движения Полученные коэффициенты указывают не только место в уравнениях
- 6. При наличии угла : 1) изменяется стреловидность правого и левого крыла по отношению к набегающему потоку,
- 7. При вращении ВС относительно оси ОХ с угловой скоростью на опускающемся полукрыле местные углы атаки увеличиваются,
- 8. При вращении ВС относительно оси OY с угловой скоростью у полукрыла идущего вперед скорость увеличивается, а
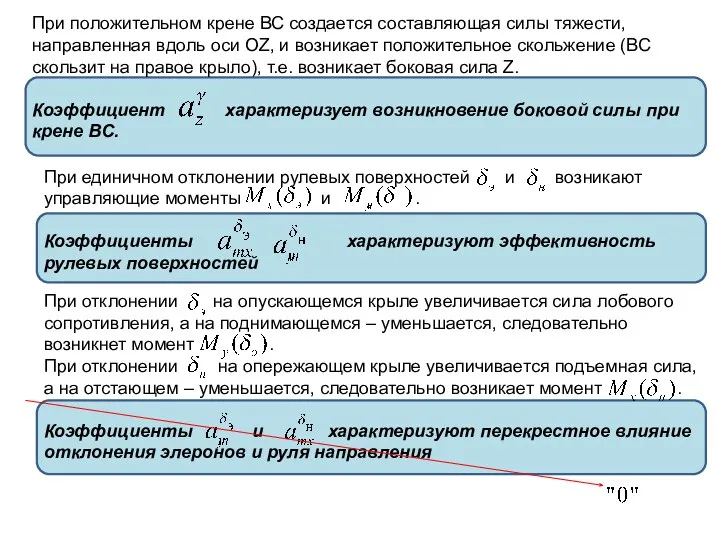
- 9. При положительном крене ВС создается составляющая силы тяжести, направленная вдоль оси OZ, и возникает положительное скольжение
- 10. Статическая устойчивость бокового движения Статическая устойчивость БД характеризуется: Боковой балансировкой Путевой устойчивостью Поперечной устойчивостью Боковая балансировка
- 11. Физический смысл: компенсировать боковую силу возникшую в результате появления угла скольжения можно отклонением ВС по крену
- 12. Для выполнения условия Уравнения 1 и 2 представляют собой условия боковой балансировки Путевая устойчивость Под путевой
- 13. Поперечная устойчивость Под поперечной устойчивостью понимается свойство ВС самостоятельно стабилизировать угол крена. При крене под действием
- 14. Для получения линейной модели бокового движения в векторно-матричной форме выполним преобразования Лапласа для исходной системы уравнений
- 15. Перейдем к матричной форме записи (ветер не учитывали) с учетом :
- 16. Определитель этой системы имеет следующую структуру: Характеристический полином системы формируется раскрытием определителя и имеет следующий вид:
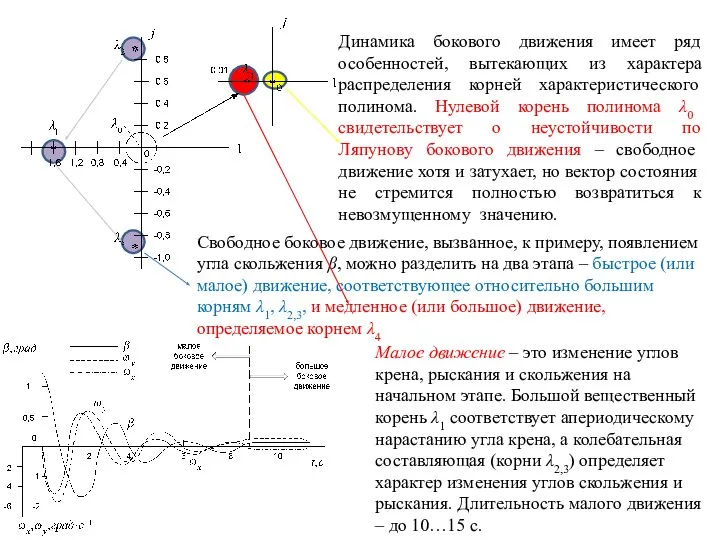
- 17. Свободное боковое движение, вызванное, к примеру, появлением угла скольжения β, можно разделить на два этапа –
- 18. К концу малого движения накапливается некоторый угол крена и сохраняется относительно малое значение угла скольжения. Траектория
- 19. 2. Передаточные функции и структурные схемы бокового движения
- 20. Математическую модель бокового движения можно представить в форме структурной схемы, если провести простые преобразования системы уравнений
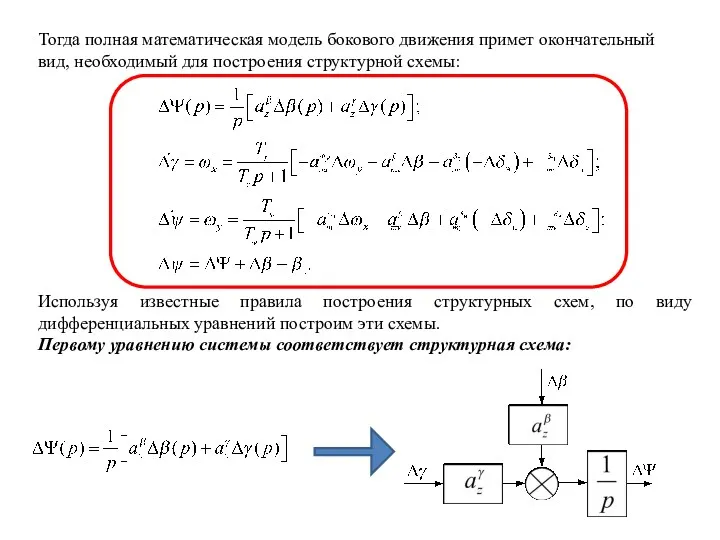
- 22. Тогда полная математическая модель бокового движения примет окончательный вид, необходимый для построения структурной схемы: Используя известные
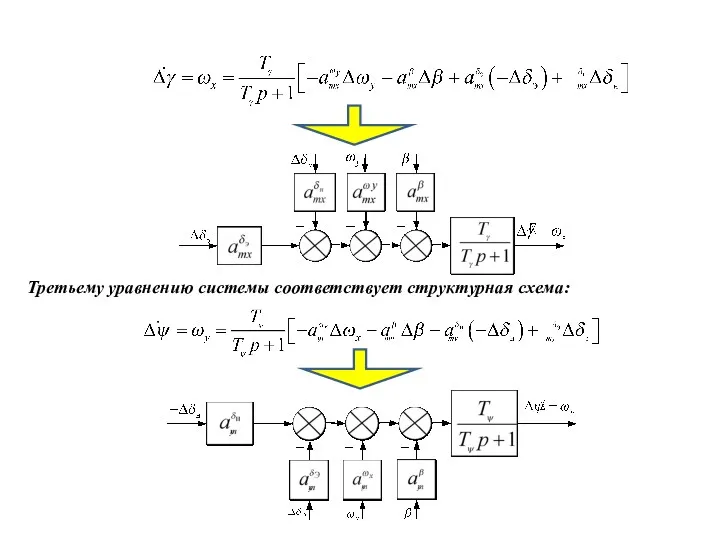
- 23. Второму уравнению системы соответствует структурная схема: Третьему уравнению системы соответствует структурная схема:
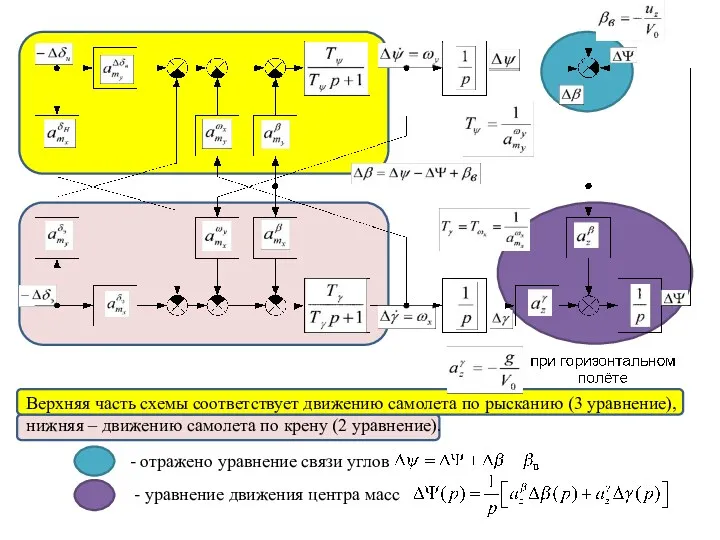
- 24. Верхняя часть схемы соответствует движению самолета по рысканию (3 уравнение), нижняя – движению самолета по крену
- 26. Скачать презентацию


















 61f4bb8105f047b8922e06e3e916ed53
61f4bb8105f047b8922e06e3e916ed53 Сила упругости. Закон Гука. Сила реакции опоры. Причина возникновения силы упругости
Сила упругости. Закон Гука. Сила реакции опоры. Причина возникновения силы упругости Лампы накаливания. Электронагревательные приборы
Лампы накаливания. Электронагревательные приборы Урок по теме: Физические величины и их измерение.
Урок по теме: Физические величины и их измерение. Тормозная система автомобиля
Тормозная система автомобиля Конференция фонда Династия 2011 год
Конференция фонда Династия 2011 год Специальная теория относительности. Постулаты теории относительности
Специальная теория относительности. Постулаты теории относительности Жидкие кристаллы
Жидкие кристаллы Презентация по теме Импульс и его сохранение
Презентация по теме Импульс и его сохранение Измерение влажности
Измерение влажности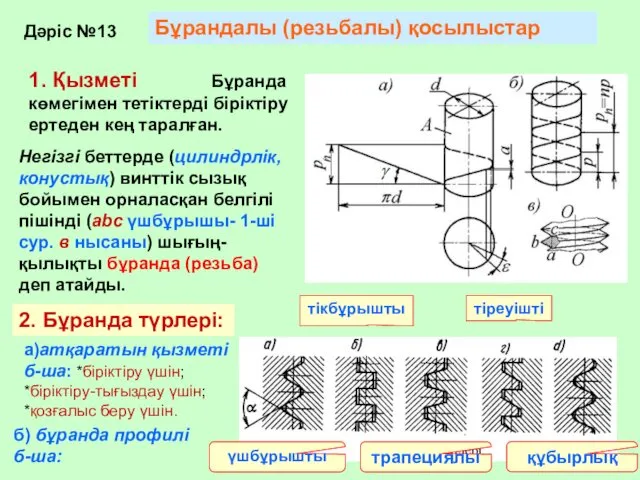 Бұрандалы қосылыстар
Бұрандалы қосылыстар Холодильные и теплонасосные установки
Холодильные и теплонасосные установки Солнечные источники энергии. Солнечные батареи
Солнечные источники энергии. Солнечные батареи Управляемый термоядерный синтез (УТС)
Управляемый термоядерный синтез (УТС) Электрический ток
Электрический ток Механические волны
Механические волны Резка металла
Резка металла Корабельные энергетические установки. Лекция 1.2
Корабельные энергетические установки. Лекция 1.2 Физические величины. Измерение физических величин 7 класс
Физические величины. Измерение физических величин 7 класс Автокөліктерді жөндеу технологиясы
Автокөліктерді жөндеу технологиясы Нефть, газ, их состав и физические свойства. Основные гипотезы происхождения нефти и газа
Нефть, газ, их состав и физические свойства. Основные гипотезы происхождения нефти и газа Электротехника и электроника. Трехфазные электрические цепи. (Лекция 8)
Электротехника и электроника. Трехфазные электрические цепи. (Лекция 8) Электрическое поле. Напряжённость электрического поля
Электрическое поле. Напряжённость электрического поля История создания швейной машинки
История создания швейной машинки Группы и определения эксплуатационных свойств
Группы и определения эксплуатационных свойств Поверхностное натяжение жидкости. Поверхностная энергия. Коэффициент поверхностного натяжения
Поверхностное натяжение жидкости. Поверхностная энергия. Коэффициент поверхностного натяжения Базові шасі техніки зв’язку. Особливості будови автомобіля КРАЗ
Базові шасі техніки зв’язку. Особливості будови автомобіля КРАЗ Зеркальные антенны. Лекция №18. АФУ
Зеркальные антенны. Лекция №18. АФУ