Содержание
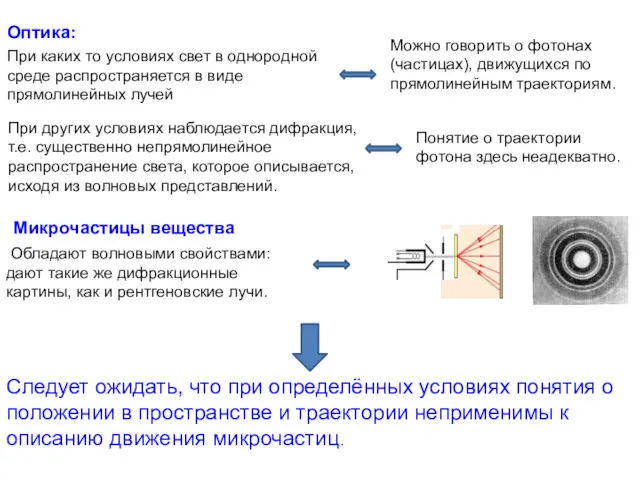
- 2. При каких то условиях свет в однородной среде распространяется в виде прямолинейных лучей При других условиях
- 3. Степень точности, с которой к частице может быть применено представление об её определённом положении в пространстве
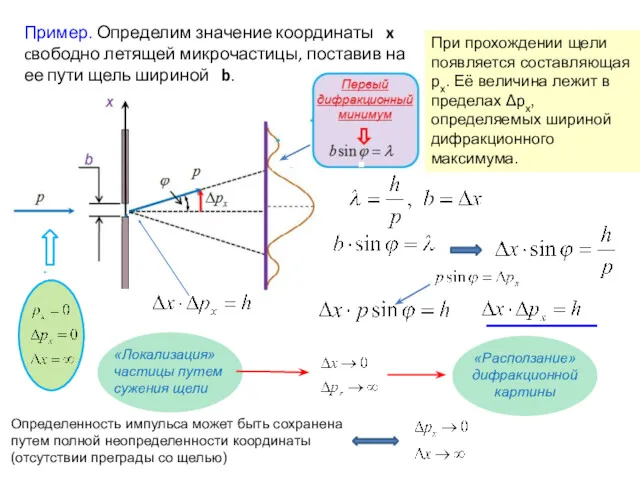
- 4. Пример. Определим значение координаты x cвободно летящей микрочастицы, поставив на ее пути щель шириной b. Определенность
- 5. Соотношение неопределенности указывает, насколько корректно применять классическую механику к объектам микромира Пример. Электрон в модели атома
- 6. Пример. Движение электрона в электронно-лучевой трубке Увеличенное изображение «пятна» от луча на экране электронно-лучевой трубки Волновые
- 7. Пример. Пылинка Пылинка – большая; у нее большая масса; она объект макромира и к ней применимы
- 8. Микрочастицы обладают волновыми свойствами. А именно, их положение в пространстве задаётся определённым вероятностным законом и этот
- 9. Уравнение Шредингера. Эрвин Шредингер (1887-1961)
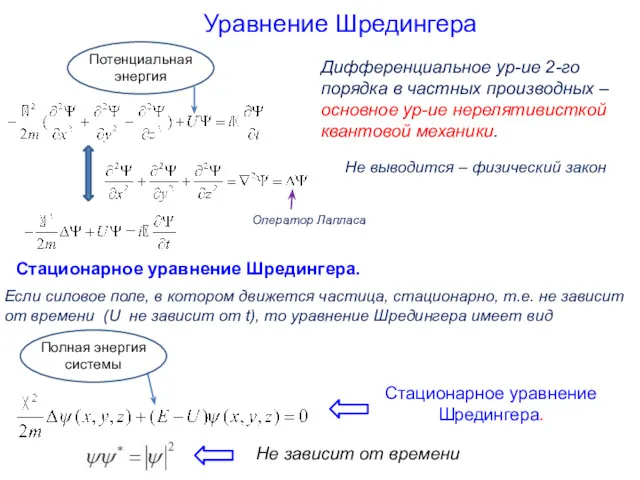
- 10. Дифференциальное ур-ие 2-го порядка в частных производных – основное ур-ие нерелятивисткой квантовой механики. Оператор Лапласа Уравнение
- 11. Частица в бесконечно глубокой одномерной потенциальной яме U – потенц.энергия частицы m – масса частицы E
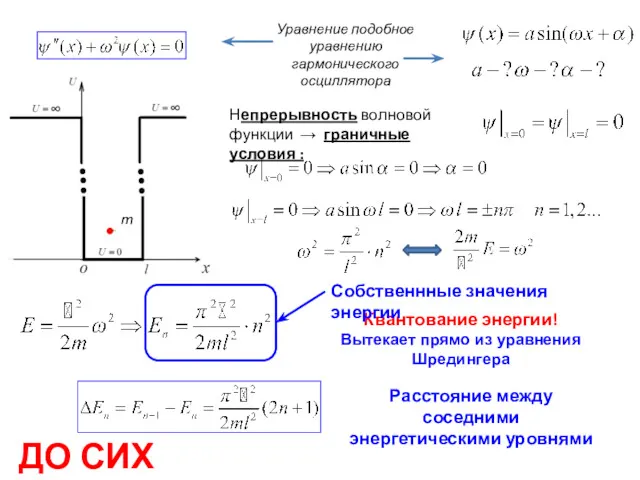
- 12. Непрерывность волновой функции → граничные условия : Уравнение подобное уравнению гармонического осциллятора Квантование энергии! Вытекает прямо
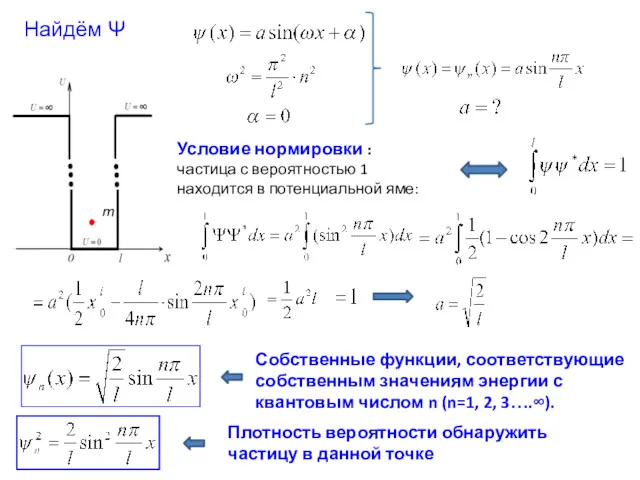
- 13. Собственные функции, соответствующие собственным значениям энергии с квантовым числом n (n=1, 2, 3….∞). Условие нормировки :
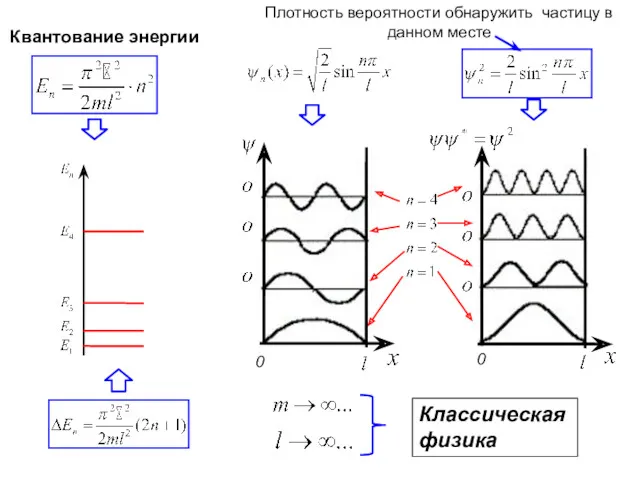
- 14. Классическая физика
- 15. Найдём масштаб квантования энергии. Пример 1: электрон, m≈10-30 кг, размер ямы l=10 см (свободный электрон в
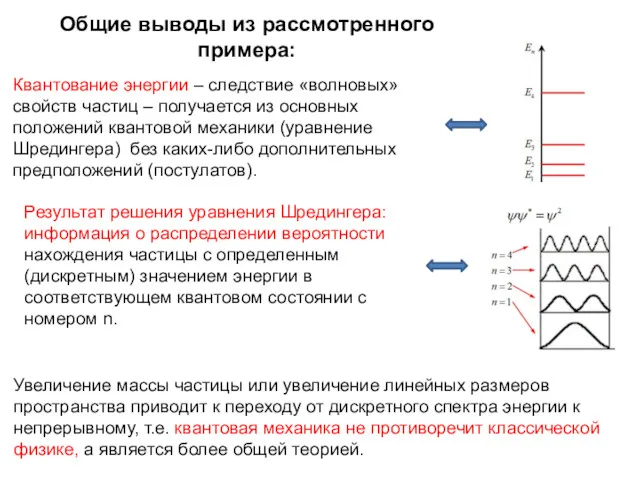
- 16. Общие выводы из рассмотренного примера: Квантование энергии – следствие «волновых» свойств частиц – получается из основных
- 17. Квантово-механическая модель атома водорода. Квантовые числа.
- 18. Система: ядро с зарядом +Ze и один электрон Решение уравнения Шредингера для электрона в центрально-симметричном поле
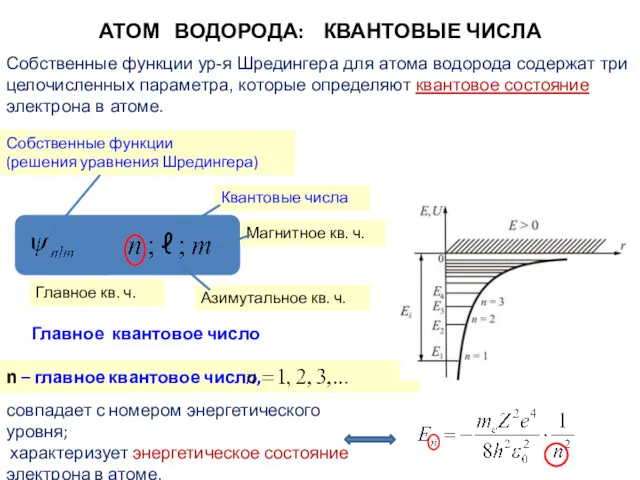
- 19. Собственные функции ур-я Шредингера для атома водорода содержат три целочисленных параметра, которые определяют квантовое состояние электрона
- 20. АТОМ ВОДОРОДА: КВАНТОВЫЕ ЧИСЛА Азимутальное квантовое число Величина момента импульса квантована (!) В отличие от модели
- 21. АТОМ ВОДОРОДА: КВАНТОВЫЕ ЧИСЛА Магнитное квантовое число Т.е. проекция момента импульса на некоторое выделенное направление принимает
- 22. m – магнитное квантовое число Одному энергетическому состоянию может соответствовать несколько квантовых состояний электрона – вырожденные
- 23. 1 4 9 АТОМ ВОДОРОДА: РАЗЛИЧНЫЕ КВАНТОВЫЕ СОСТОЯНИЯ, ОРБИТАЛИ
- 25. Скачать презентацию














 Интерференция света. (Лекция 11)
Интерференция света. (Лекция 11) Происхождение элементов
Происхождение элементов Кроссворд
Кроссворд Молекулярно-кинетическая теория строения вещества (МКТ)
Молекулярно-кинетическая теория строения вещества (МКТ) Кинематика тела. Лекция 7
Кинематика тела. Лекция 7 тест по состояниям вещества 8 класс
тест по состояниям вещества 8 класс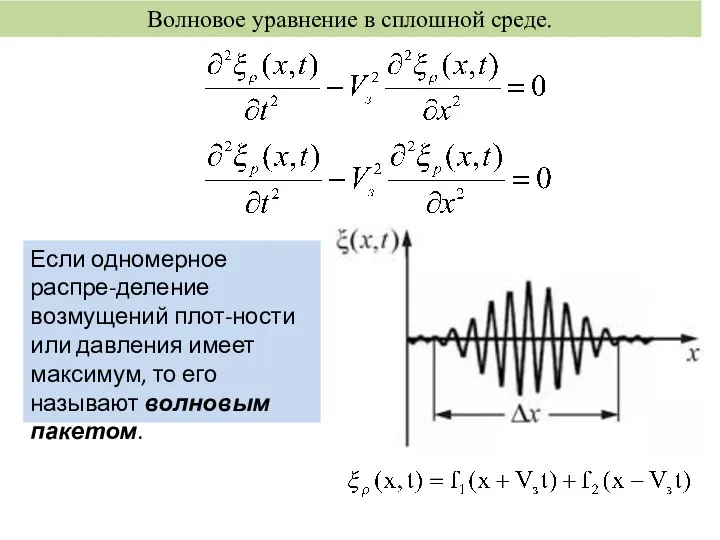 Волновое уравнение в сплошной среде
Волновое уравнение в сплошной среде Электромагнитные волны
Электромагнитные волны Методы исследования наносистем и наноматериалов. Классификация физико-химических методов исследования
Методы исследования наносистем и наноматериалов. Классификация физико-химических методов исследования Презентация к уроку физики в 8 классе: Обобщение по теме Агрегатные состояния вещества.
Презентация к уроку физики в 8 классе: Обобщение по теме Агрегатные состояния вещества. Магнитные материалы. Магнитное поле в веществе
Магнитные материалы. Магнитное поле в веществе Урок физики 8 класс Испарение и конденсация
Урок физики 8 класс Испарение и конденсация Аеродинамічні характеристики літака. Аеродинамічне компонування літака. (Лекція 7.4.1)
Аеродинамічні характеристики літака. Аеродинамічне компонування літака. (Лекція 7.4.1) 03.21г. Типы спектров. Спектральный анализ
03.21г. Типы спектров. Спектральный анализ Фундаментальные взаимодействия
Фундаментальные взаимодействия Презентация к уроку Водород, 5 класс, предмет Физика и химия
Презентация к уроку Водород, 5 класс, предмет Физика и химия Закон Гука
Закон Гука Лабораторная работа №2. Измерение массы тела на рычажных весах
Лабораторная работа №2. Измерение массы тела на рычажных весах Электризация тел. Два рода зарядов
Электризация тел. Два рода зарядов Поляризация поперечных волн. Поляризация света. Дисперсия света. Виды спектров
Поляризация поперечных волн. Поляризация света. Дисперсия света. Виды спектров Батарейка своими руками
Батарейка своими руками Качество электроэнергии
Качество электроэнергии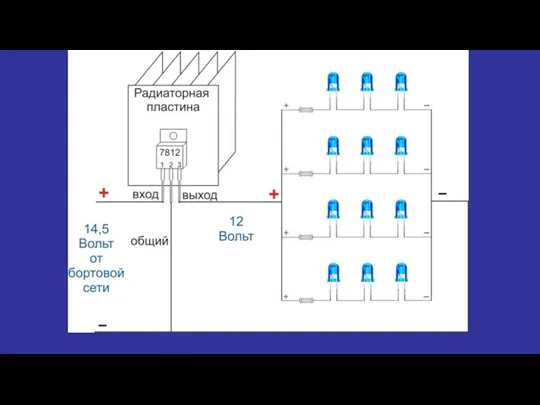 Электрическая схема светильника с регулировкой мощности
Электрическая схема светильника с регулировкой мощности Шлифовальные станки. (Тема 7)
Шлифовальные станки. (Тема 7) Электромагнитная картина мира
Электромагнитная картина мира Курсовая работа по теоретической механике “Динамика кулисного механизма”
Курсовая работа по теоретической механике “Динамика кулисного механизма”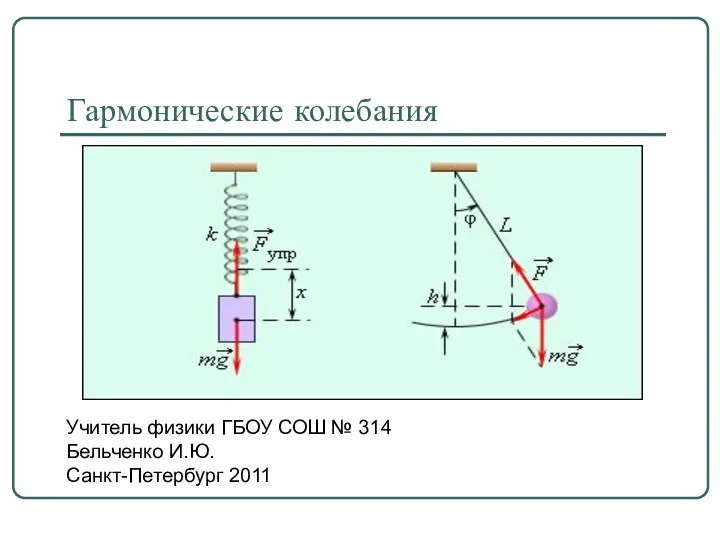 Гармонические колебания
Гармонические колебания Работа силы Ампера. Магнитный поток. Явление электромагнитной индукции. Закон электромагнитной индукции. Правило Ленца
Работа силы Ампера. Магнитный поток. Явление электромагнитной индукции. Закон электромагнитной индукции. Правило Ленца