Содержание
- 2. Условие задачи Рассчитать все переходные токи цепи и переходное напряжение на катушке индуктивности, построить временные зависимости
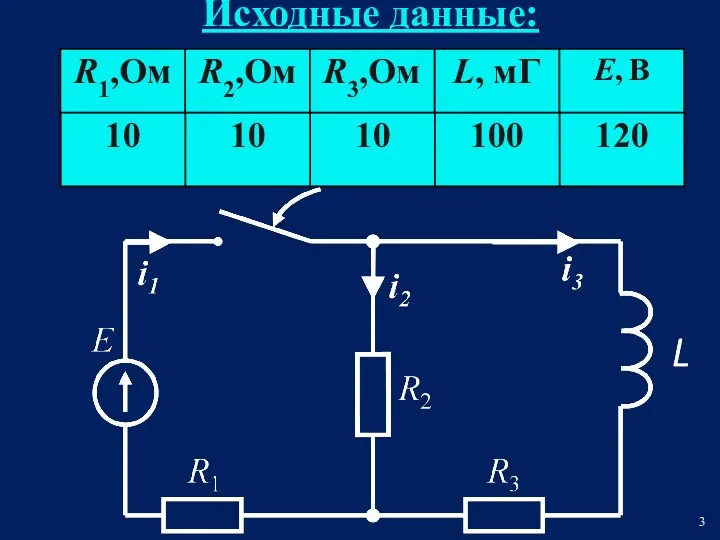
- 3. Исходные данные:
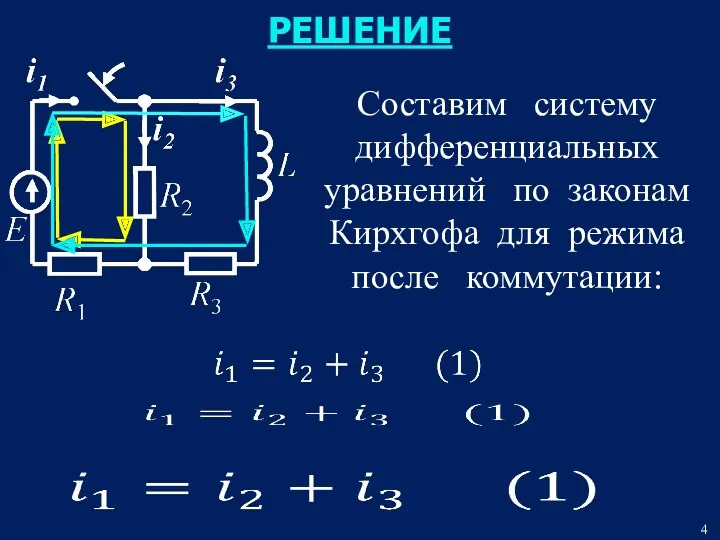
- 4. РЕШЕНИЕ Составим систему дифференциальных уравнений по законам Кирхгофа для режима после коммутации:
- 5. Принимаем за базовое уравнение (3) и при помощи уравнений (1) и (2) выразим ток i1 через
- 7. Уравнение (5) подставим в уравнение (3)
- 8. В полученное уравнение подставим числовые значения:
- 9. Искомый ток определяется суммой двух решений: принуждённой и свободной составляющими:
- 10. Искомый ток в установившемся после коммутационном режиме является постоянным, так как источник ЭДС – постоянный во
- 11. Второй способ определения установившегося тока Рассмотрим заданную электрическую цепь после коммутации в установившемся режиме. Тогда:
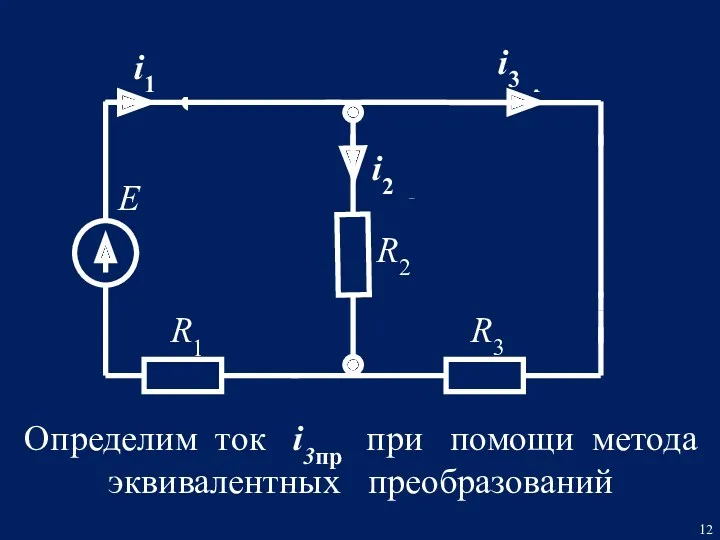
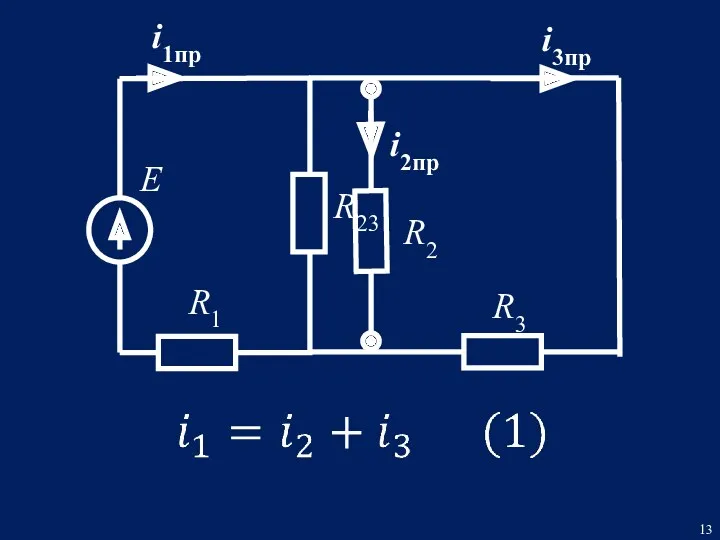
- 12. Е R3 R2 L R1 i1пр i2пр. i3пр. Определим ток i3пр при помощи метода эквивалентных преобразований
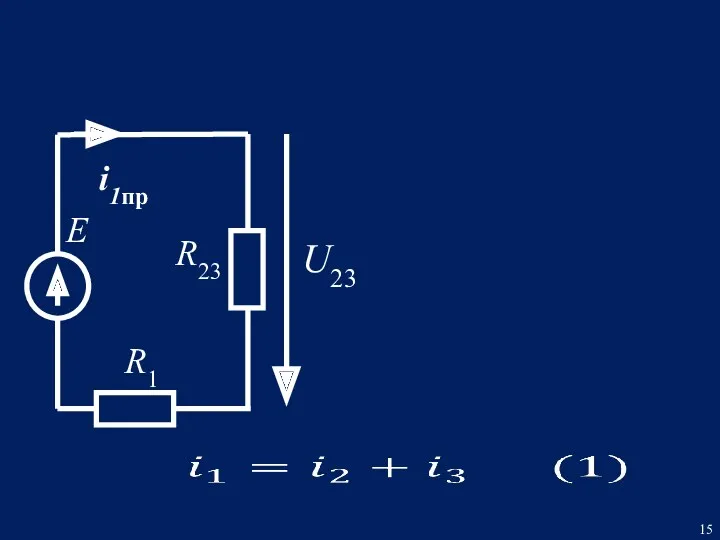
- 13. Е R1 i1пр
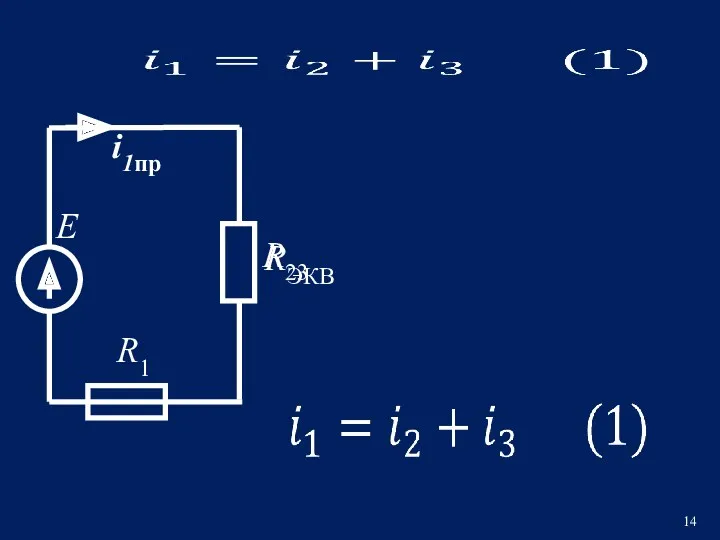
- 14. Е R1 i1пр R23 RЭКВ
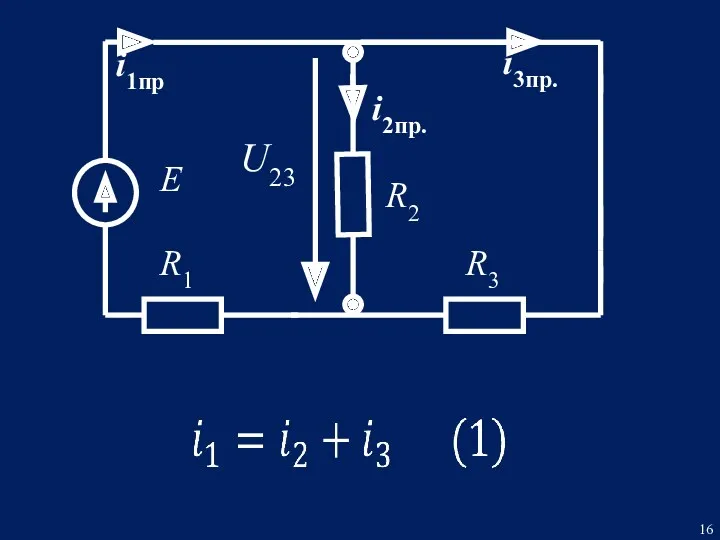
- 16. i1пр i3пр.
- 17. Определяем корень алгебраического уравнения: Уравнение (6) приводим к однородному и алгебраизируем его: Расчёт cвободной составляющей 0
- 18. Вид решения для свободной составляющей тока: Полное решение для искомого тока:
- 19. Определяем постоянную интегрирования А при помощи начальных условий и закона коммутации. В соответствии с I законом
- 20. Тогда для момента времени t = 0 уравнение (7) приобретает следующий вид: В данном случае, так
- 21. А = – 4 ×0 Полное решение искомого тока i3 (t) = 4 – 4е –150t
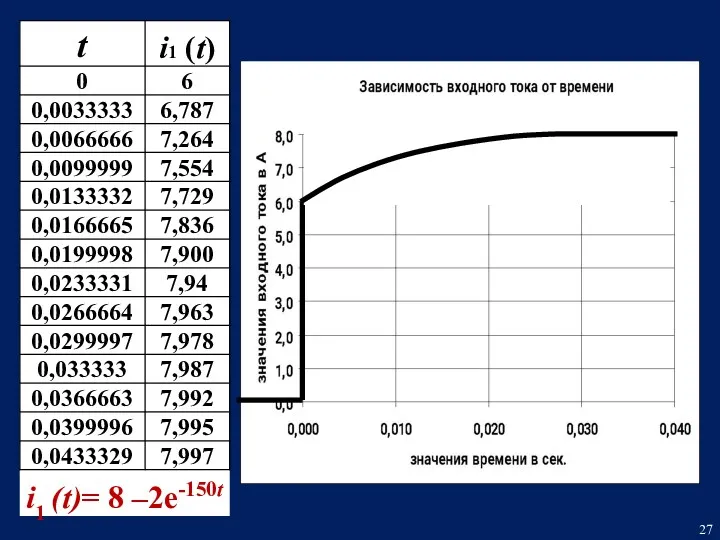
- 22. Определим остальные токи схемы при помощи исходной системы уравнений. i1 (t) = 8 – 2е –150t
- 23. i2 = 12 – 8 + 2е –150t Из уравнения (4) определим ток i2 : i2
- 24. i1 (t) = 8 – 2е –150t i2 (t) = 4 + 2е –150t i3 (t)
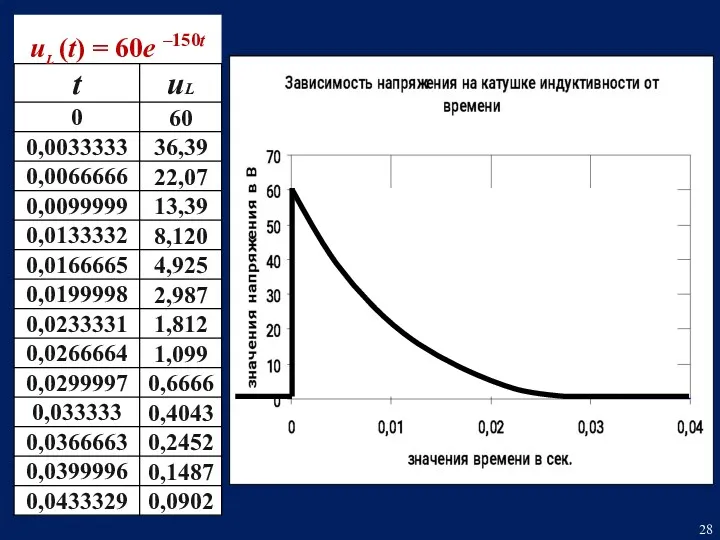
- 25. Определим закон изменения напряжения на катушке индуктивности uL (t) = 60е –150t i3 (t) = 4
- 26. Шаг изменения времени для построения графических зависимостей: Определим время переходного процесса:
- 29. ПРИМЕР ВЫПОЛНЕНИЯ РАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ №2
- 30. Методические указания с требованиями по оформлению и вариантами расчётно-графической работы приведены на сайте http:// vinokurovuniver.jimdo. com
- 31. Номер варианта определяется трёмя последними цифрами зачётной книжки студента
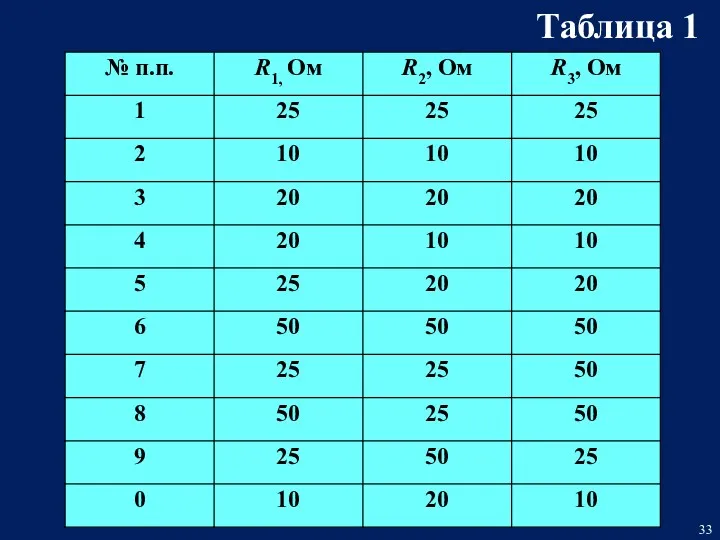
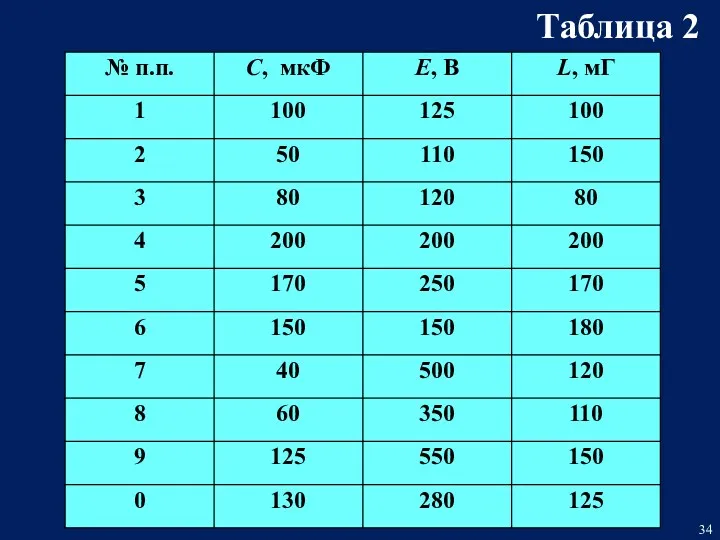
- 32. первая цифра — соответствует номеру строки из таблицы 1 вторая цифра — соответствует номеру строки из
- 33. Таблица 1
- 34. Таблица 2
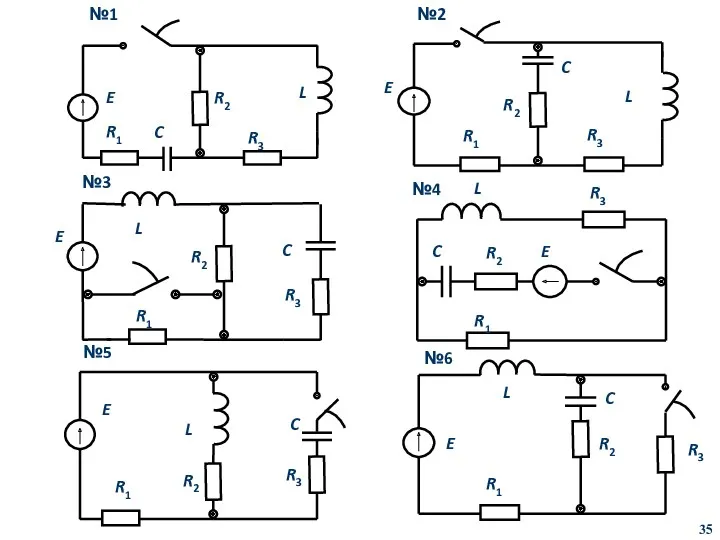
- 35. R1 E C R2 R3 L №1 E R1 L C R2 R3 №6 L C
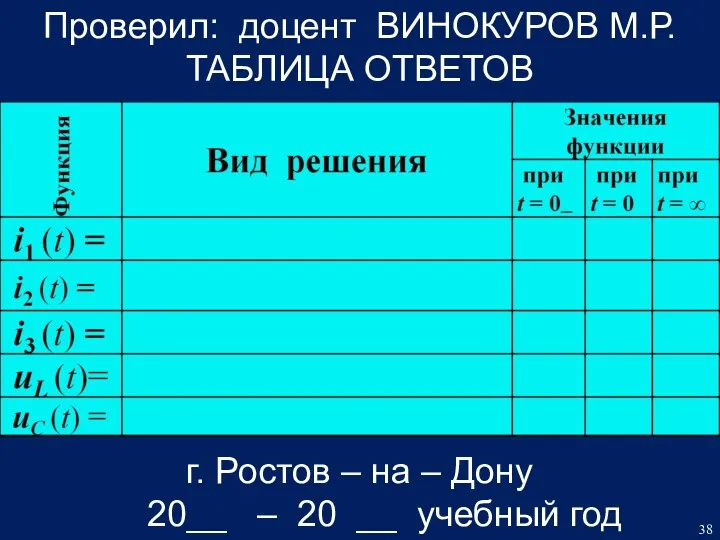
- 38. Проверил: доцент ВИНОКУРОВ М.Р. ТАБЛИЦА ОТВЕТОВ г. Ростов – на – Дону 20__ – 20 __
- 39. Содержание работы: 1. Рассчитать все переходные токи цепи и переходные напряжения на конденсаторе и на катушке
- 40. 3. Построить временные зависимости в одной системе координат по результатам, полученными двумя методами для: тока в
- 41. В качестве примера рассмотрим вариант задачи со следующими исходными данными: R1 = 20 Ом; R2 =
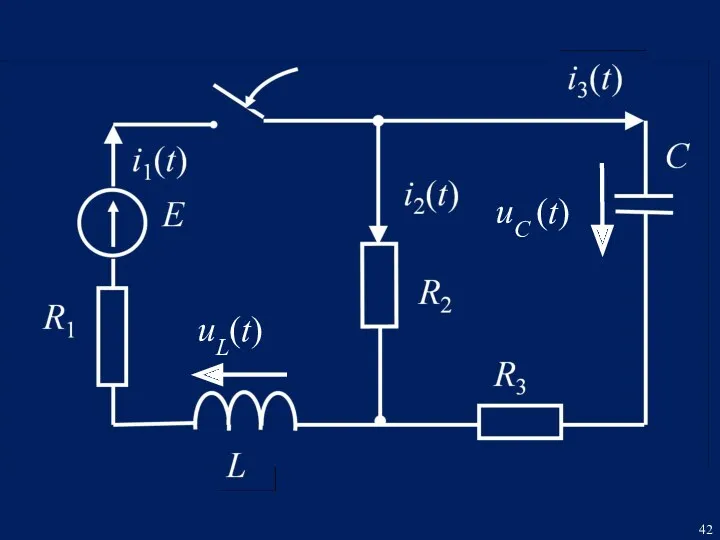
- 42. uL(t) uC (t)
- 43. 1. Расчёт всех переходных токов цепи и переходных напряжений на конденсаторе и на катушке индуктивности классическим
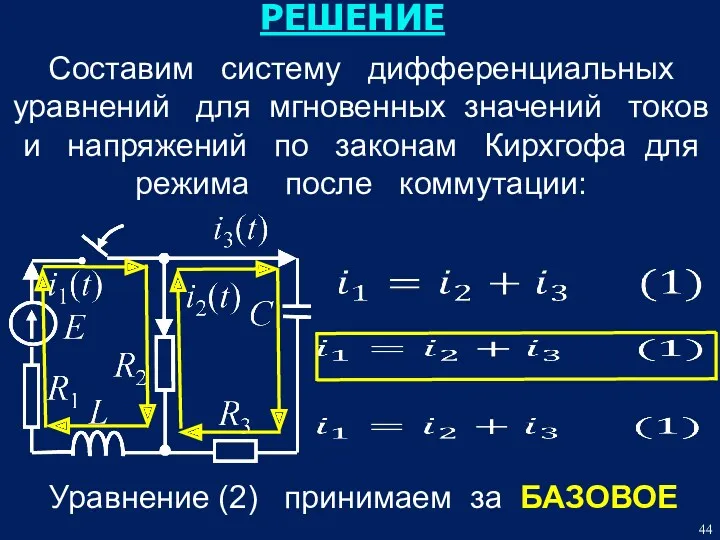
- 44. РЕШЕНИЕ Составим систему дифференциальных уравнений для мгновенных значений токов и напряжений по законам Кирхгофа для режима
- 45. Cформируем неоднородное дифференциальное уравнение относительно переменной uC (t) Для этого установим связь всех переменных уравнения с
- 46. Выразим ток i2 из уравнения (3) С учётом того, что
- 49. Выразим напряжение на катушке индуктивности:
- 51. Группируем полученное уравнение и формируем неоднородное дифференциальное уравнение 2 порядка относительно напряжения на конденсаторе: С учётом
- 52. Полное решение для напряжения на конденсаторе:
- 53. Исходное дифференциальное уравнение в этом случае принимает вид: Расчёт принуждённой составляющей Так как источник ЭДС –
- 55. Расчёт свободной составляющей Алгебраизируем однородное дифференциальное уравнение: Преобразуем исходное неоднородное дифференциальное уравнение к однородному
- 56. Решение квадратного уравнения вида:
- 58. Комплексно-сопряжённые корни указывают на колебательный или периодический затухающий переходный режим
- 59. Вид решения для свободной составляющей и полное решение для uc Полученное решение для нулевого момента времени
- 60. В качестве такого уравнения может быть использовано уравнение для тока, протекающего в ветви с конденсатором:
- 61. Для нулевого момента времени ( t = 0) :
- 62. Система уравнений, состоящая из уравнений (4) и (5), позволяет определить постоянные интегрирования А и γ :
- 63. Если корни дифференциального уравнения отрицательные, вещественные и разные, то такой переходный процесс называется апериодическим НАПРИМЕР:
- 64. Вид решения для свободной составляющей и полное решение для uc в данном случае имеют вид: Для
- 65. В качестве такого уравнения и в данном случае может быть использовано уравнение для тока, протекающего в
- 66. Для нулевого момента времени ( t = 0) :
- 68. Для совместного решения этих уравнений [ как и уравнений (4) и (5)] необходимо определить значения величин
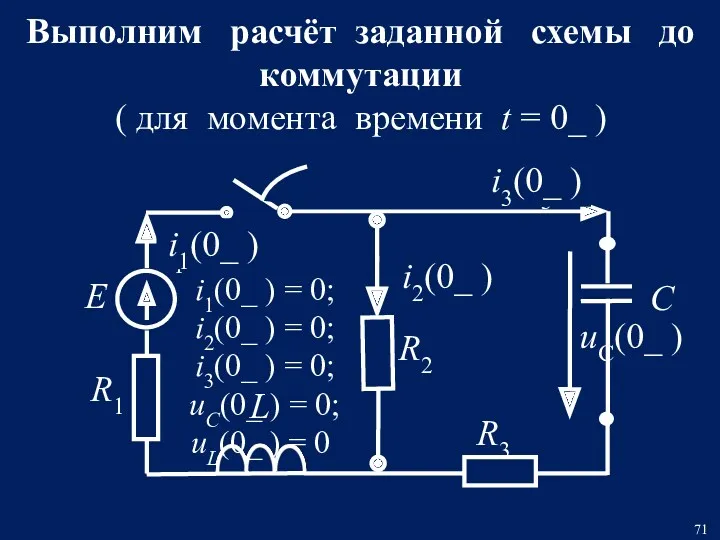
- 71. Е R1 R2 R3 i1(t) i2(t) i3(t) Выполним расчёт заданной схемы до коммутации ( для момента
- 72. В данном случае искомые независимые начальные условия являются нулевыми, т.е.: uC(0_ ) = 0; i1(0_ )
- 73. Исходная система уравнений для момента времени t = 0 может быть преобразована с учётом независимых начальных
- 74. Из уравнения (1) Из уравнения (3)
- 75. Из уравнения (1): Из уравнения (2): i2 (0) = – i3(0) = 0
- 76. По результатам расчёта приведённой схемы в момент коммутации (t = 0 ) получаем следующие результаты: i1(0)
- 77. Уравнения (4) и (5) могут быть теперь решены совместно: 0 = – 0,0268 × A ×
- 78. 0 = – 0,0268 ×A× sinγ + 0,02412 ×A× cosγ 0 = 1,608 – 1,447ctg γ
- 85. 2. Вывод системы дифференциальных уравнений для метода переменных состояния и расчёт тока в катушке индуктивности и
- 86. на каждом из которых значение переменной определяется с помощью линейной комбинации некоторых вспомогательных функций с постоянными
- 87. Достаточно получить следующие функциональные зависимости:
- 90. РЕШЕНИЕ
- 91. Выразим ток i2 из уравнения (1) Подставим ток i2 в уравнение (3)
- 93. k – номер шага итерации k = 0, 1, 2, ……. n
- 94. После подстановки числовых значений получим:
- 100. С помощью специализированной программы выполняется совместное решение полученных итерационных уравнений: При следующих начальных условиях:
- 101. Порядок обращения к программе
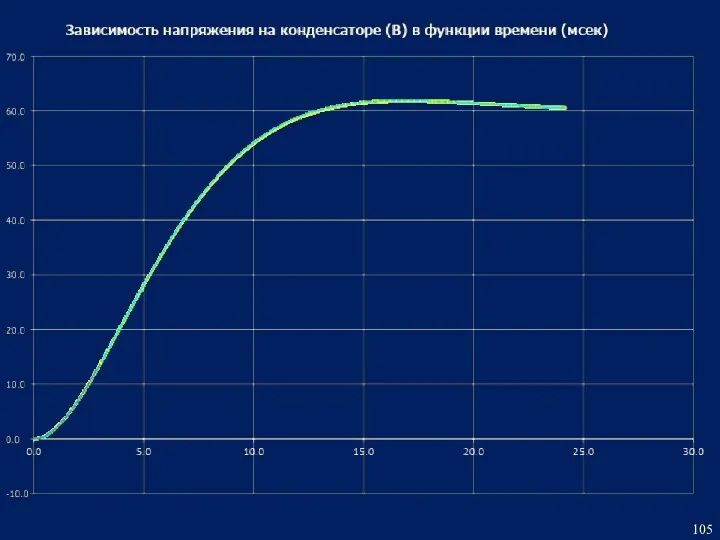
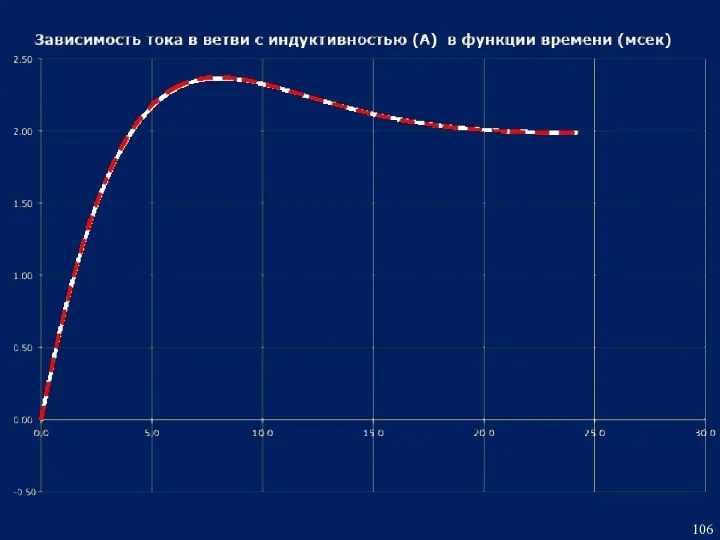
- 102. 3. Построение временных зависимостей напряжения на конденсаторе и тока в ветви с индуктивностью в одной системе
- 103. (программа КПП)
- 104. При возникновении апериодического переходного процесса (АПП) следует обратиться к соответствующей программе и ввести значения требуемых коэффициентов
- 108. Скачать презентацию


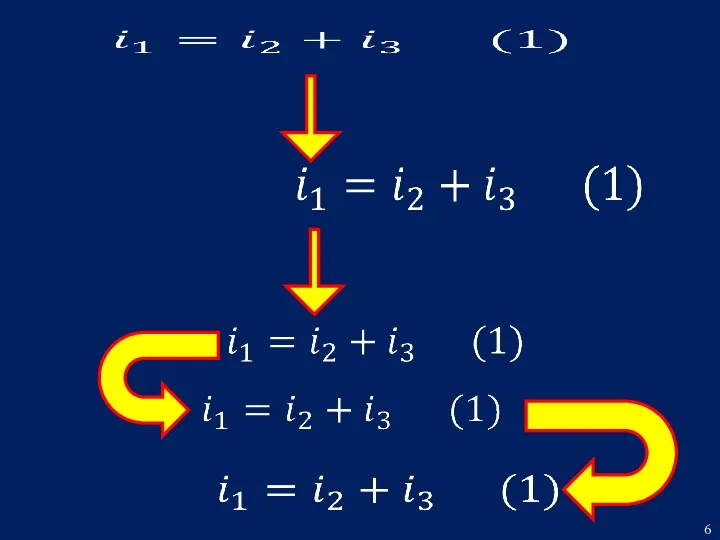


























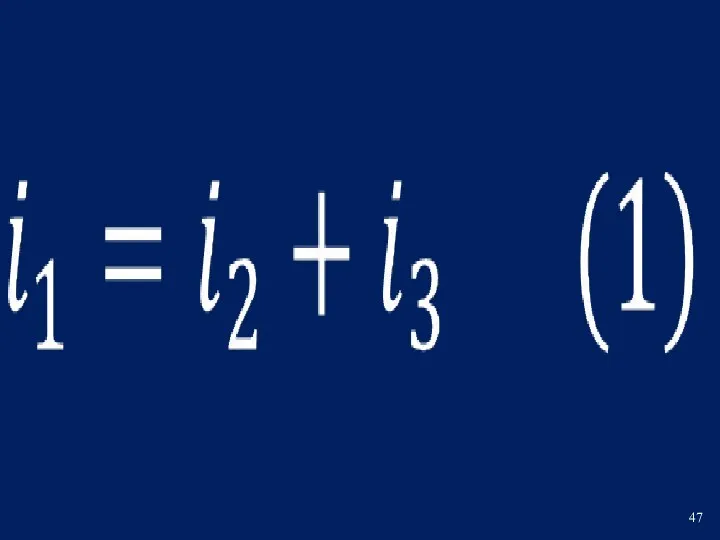
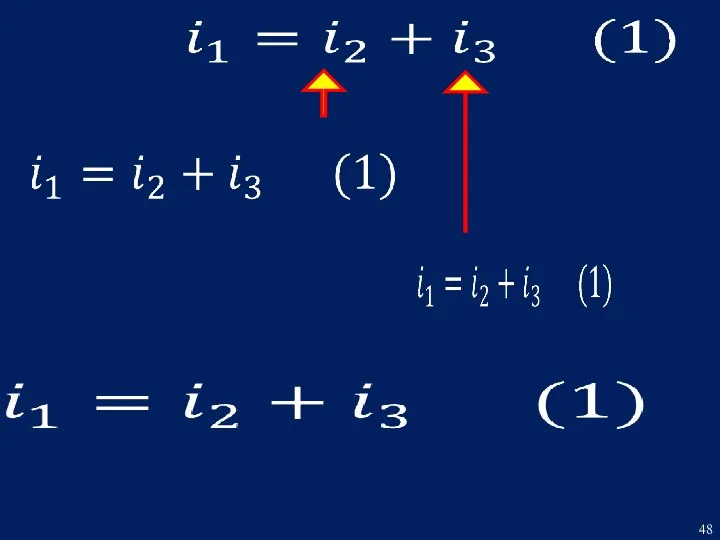

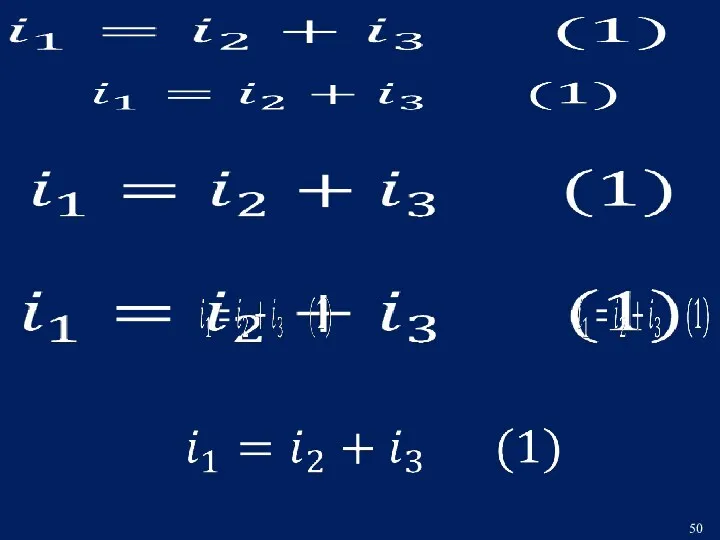



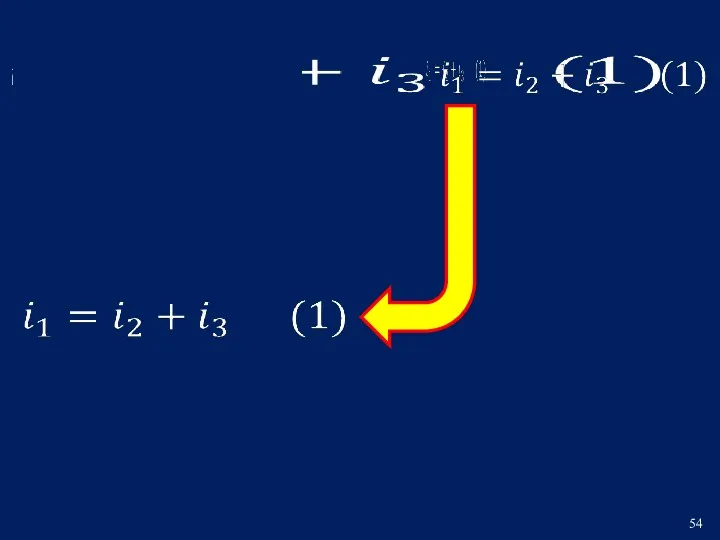

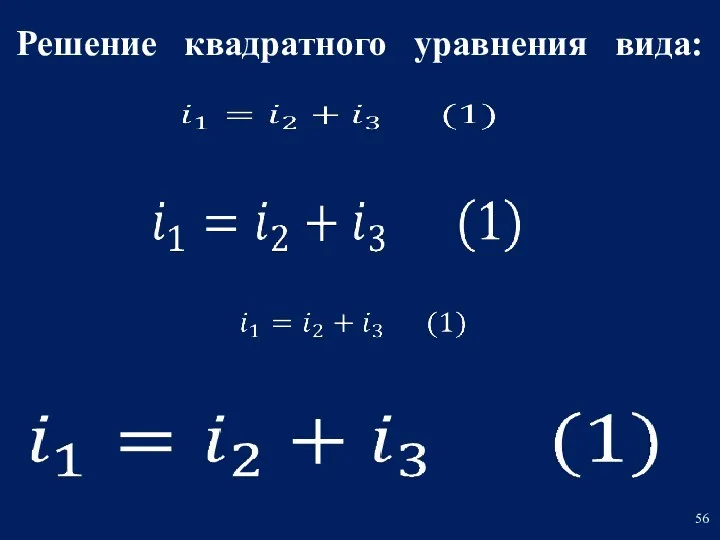










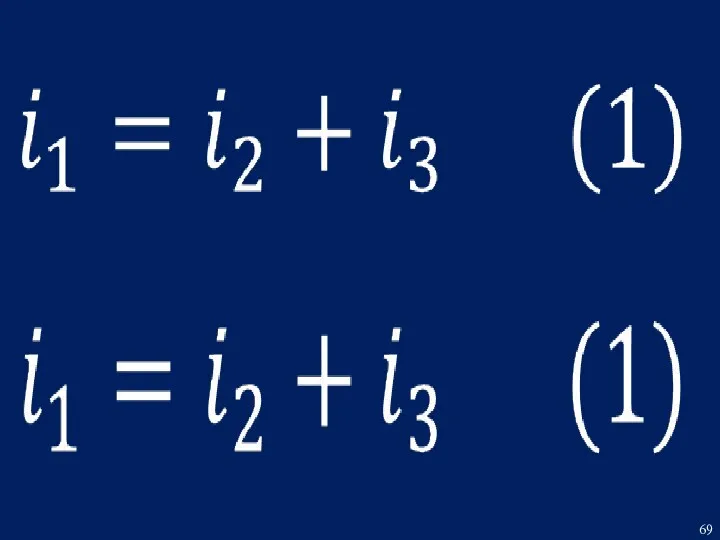
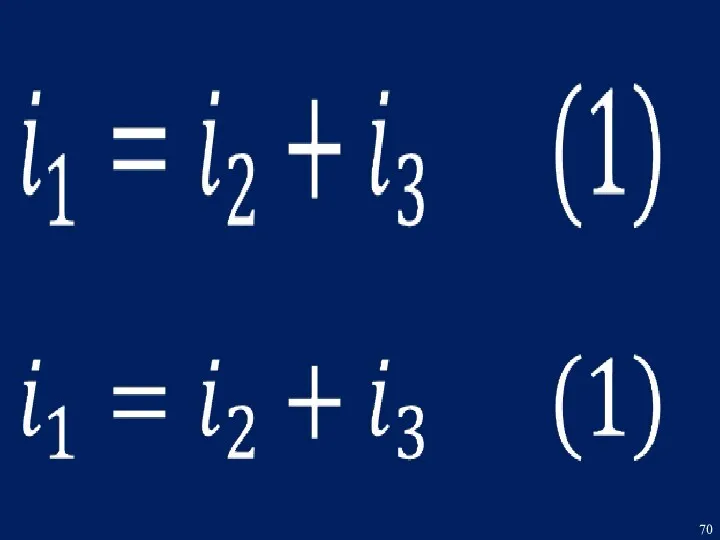



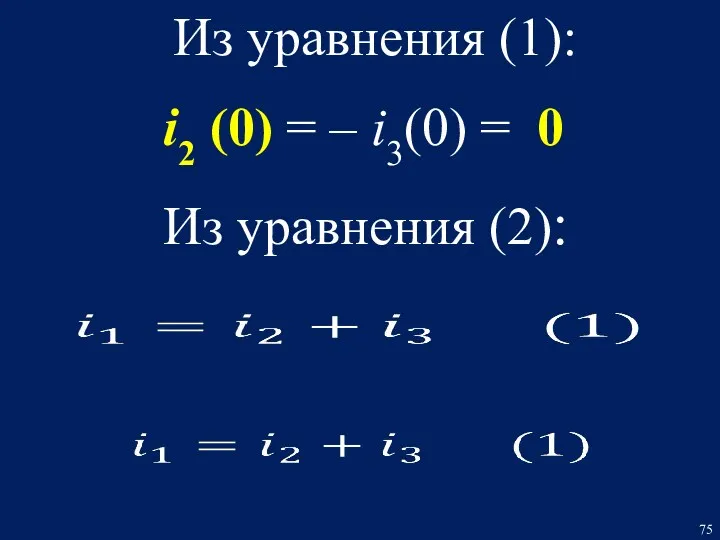


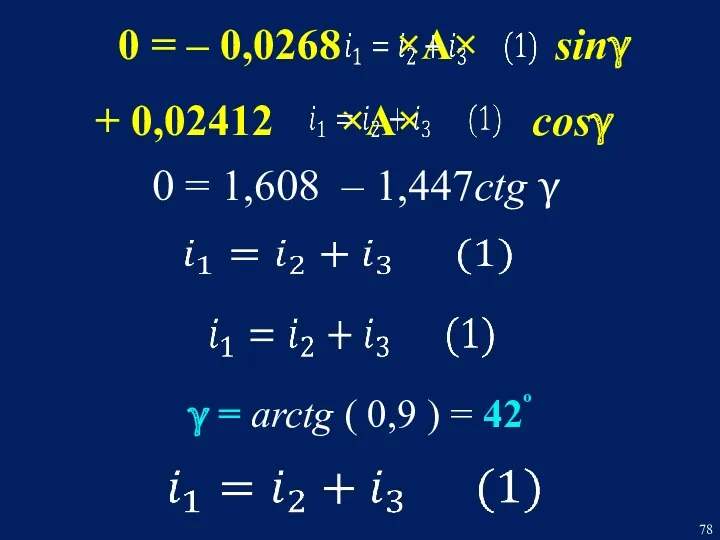

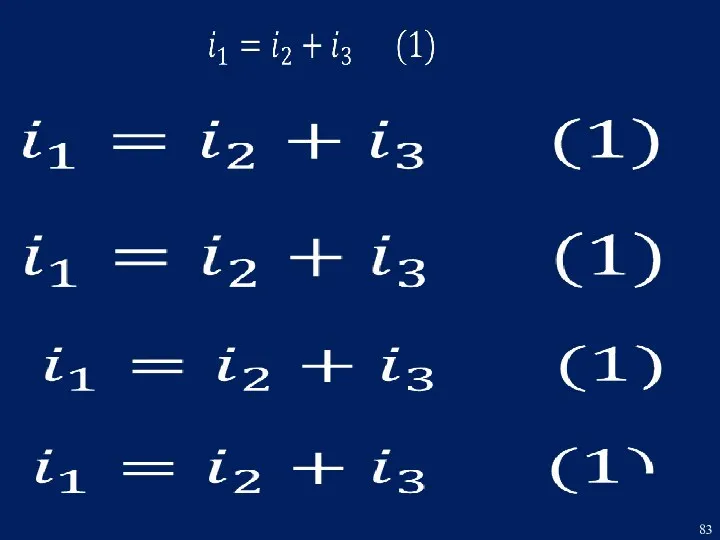
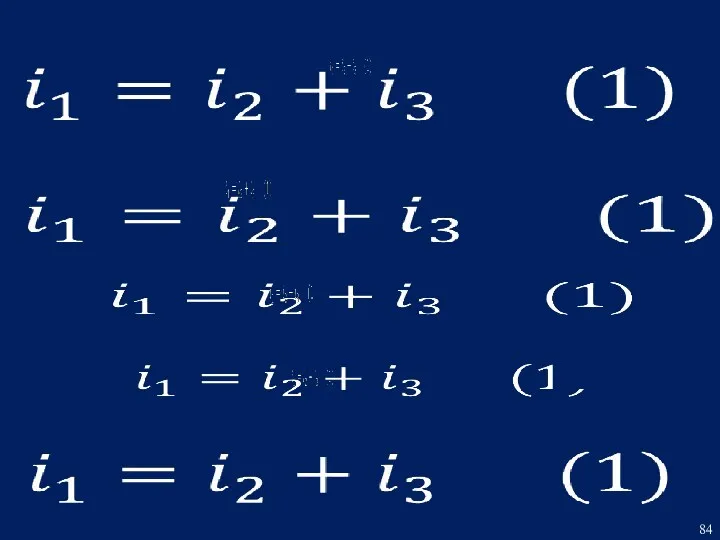



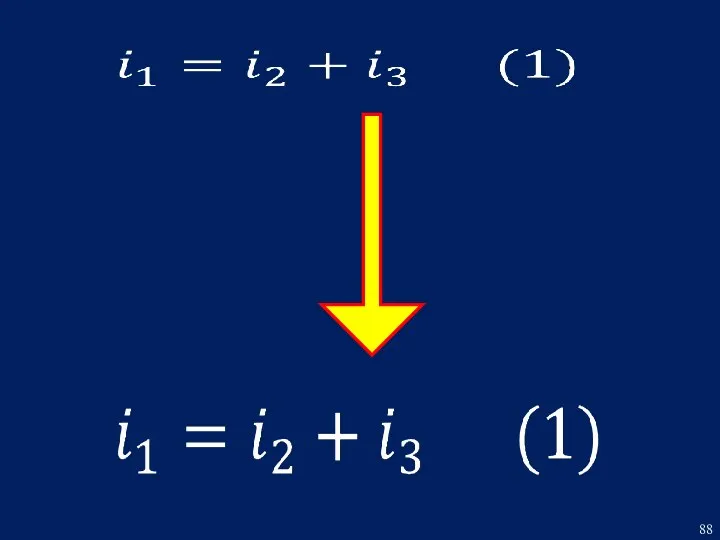
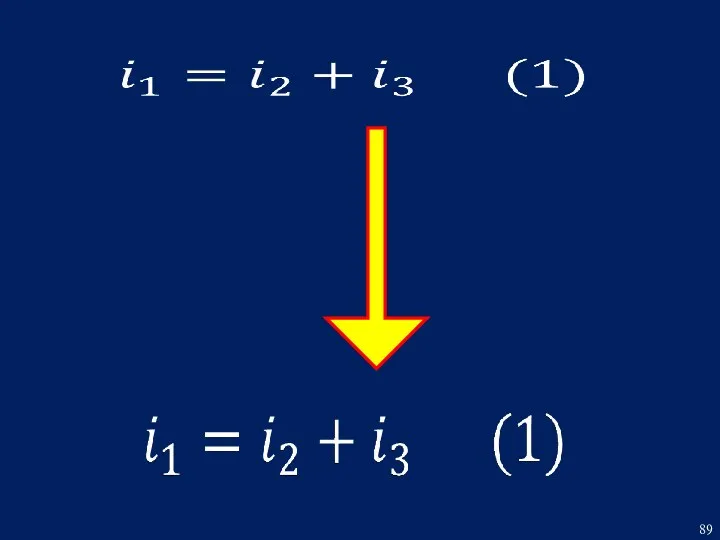




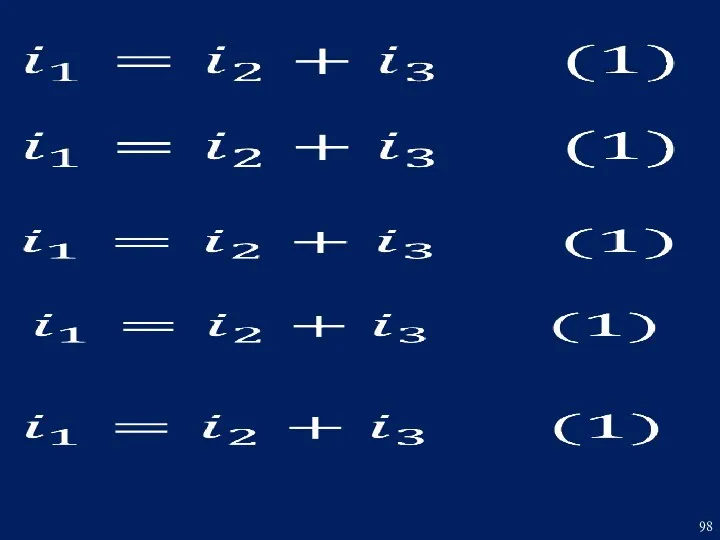






 Урок + презентация. Тема: Сила Ампера
Урок + презентация. Тема: Сила Ампера Изучение прецессии гироскопа
Изучение прецессии гироскопа Основы физики деления ядер
Основы физики деления ядер Методи аналізу лінійних електронних кіл
Методи аналізу лінійних електронних кіл Газовые законы
Газовые законы Интеллектуальная минутка по теме электродинамика
Интеллектуальная минутка по теме электродинамика Стандартная модель. Космогония современного мира
Стандартная модель. Космогония современного мира Діелектрики та провідники в електростатичному полі
Діелектрики та провідники в електростатичному полі Презентация 7 кл. Измерение атмосферного давления
Презентация 7 кл. Измерение атмосферного давления Тепловые и холодильные машины. Второе начало термодинамики
Тепловые и холодильные машины. Второе начало термодинамики Развитие наглядно – образного мышления у обучающихся с нарушениями зрения на уроках физики
Развитие наглядно – образного мышления у обучающихся с нарушениями зрения на уроках физики Шарль Огюстен де Кулон
Шарль Огюстен де Кулон Закони динаміки. Перший закон Ньютона. Інерціальні системи відліку
Закони динаміки. Перший закон Ньютона. Інерціальні системи відліку Теоретические основы электротехники
Теоретические основы электротехники Квантовая оптика. Тепловое излучение
Квантовая оптика. Тепловое излучение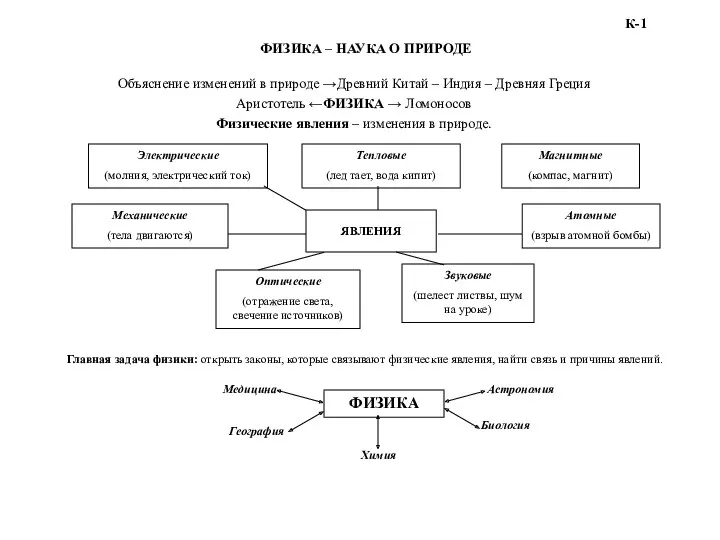 Физика – наука о природе
Физика – наука о природе Равномерное и неравномерное прямолинейное движение
Равномерное и неравномерное прямолинейное движение Влажность воздуха
Влажность воздуха Шкала электромагнитных излучений
Шкала электромагнитных излучений Портфолио учителя физики Бушмакиной Е. С.
Портфолио учителя физики Бушмакиной Е. С. Центр тяжести. Равновесие тел
Центр тяжести. Равновесие тел Сила тяжести. Движение в поле силы тяжести
Сила тяжести. Движение в поле силы тяжести Разрушение материалов
Разрушение материалов Магнитные свойства вещества
Магнитные свойства вещества Оптимальная оценка неэнергетического параметра сигнала. Тема 4: часть 2
Оптимальная оценка неэнергетического параметра сигнала. Тема 4: часть 2 Electrical potentials of the cell
Electrical potentials of the cell Дифракция света. Лекция 3
Дифракция света. Лекция 3 Теория атома водорода по Бору. Элементы квантовой механики
Теория атома водорода по Бору. Элементы квантовой механики