Содержание
- 2. На предыдущих лекциях мы обсудили вопросы дискретной фильтрации случайных последовательностей .
- 3. Содержание Случайные процессы и методы их описания. Понятие формирующего фильтра и его свойства. Постановка и общее
- 4. Случайные процессы и методы их описания
- 5. Случайным процессом x(t) в скалярном случае называется такая функция времени t, значение которой при любом фиксированном
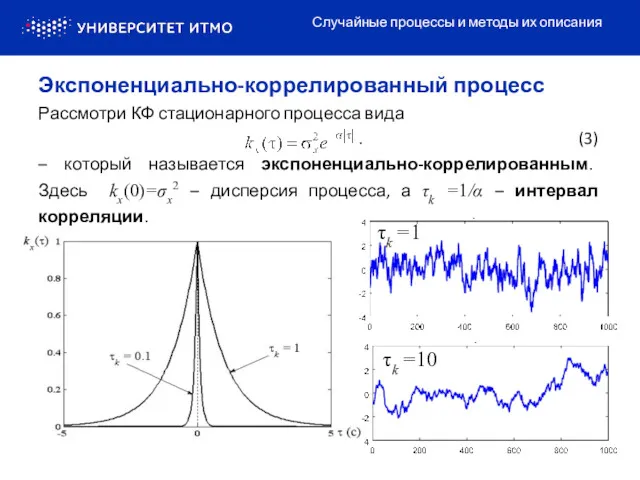
- 6. Рассмотри КФ стационарного процесса вида . (3) – который называется экспоненциально-коррелированным. Здесь kx(0)=σx2 – дисперсия процесса,
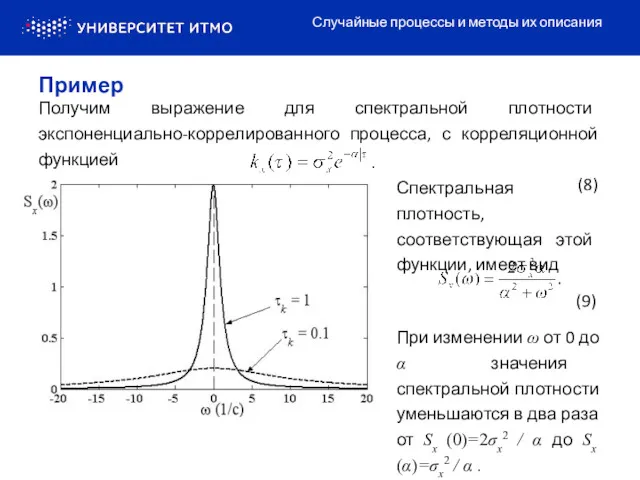
- 7. Спектральная плотность также используется для описания стационарных процессов и представляет собой преобразование Фурье от КФ .
- 8. Спектральная плотность, соответствующая этой функции, имеет вид (9) При изменении ω от 0 до α значения
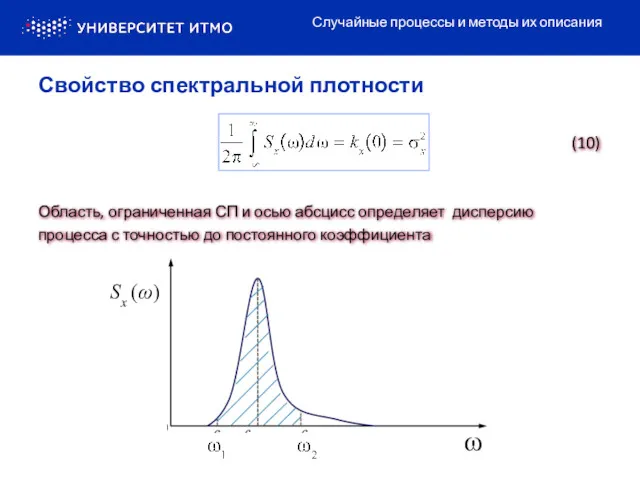
- 9. ω Sx (ω) Область, ограниченная СП и осью абсцисс определяет дисперсию процесса с точностью до постоянного
- 10. Процесс с постоянной спектральной плотностью во всем диапазоне частот, для которого Sx (ω)=Q, называется белым шумом
- 12. Скачать презентацию






 Айнымалы ток тізбегіндегі актив кедергі. (Лекция 14)
Айнымалы ток тізбегіндегі актив кедергі. (Лекция 14) Переменный электрический ток
Переменный электрический ток Презентация к внеклассному мероприятию
Презентация к внеклассному мероприятию Урок-путешествие в страну Электричество
Урок-путешествие в страну Электричество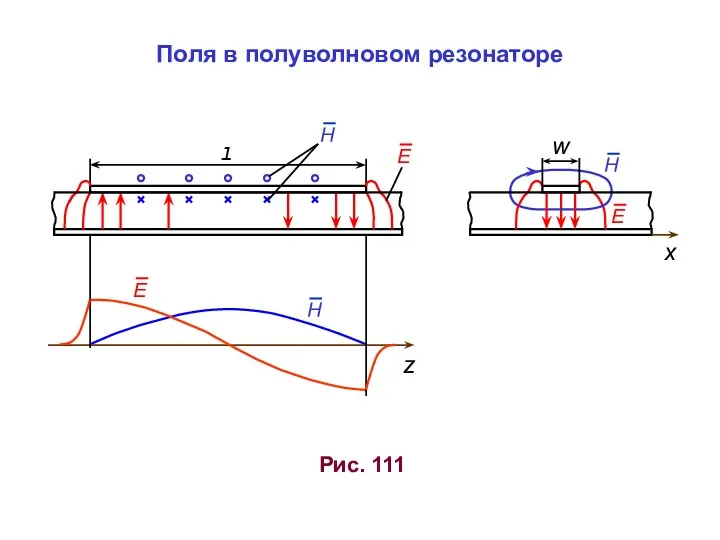 Поля в полуволновом резонаторе
Поля в полуволновом резонаторе Эксплуатация оборудования для ремонта агрегатов автомобиля. Ремонт ГБЦ (урок 17)
Эксплуатация оборудования для ремонта агрегатов автомобиля. Ремонт ГБЦ (урок 17) Рівноприскорений прямолінійний рух. Прискорення
Рівноприскорений прямолінійний рух. Прискорення Взаимодействие магнитного поля и проводников с током
Взаимодействие магнитного поля и проводников с током Методы и средства измерения полосы пропускания и дисперсии оптических волокон
Методы и средства измерения полосы пропускания и дисперсии оптических волокон Квантовая физика. Тема № 5
Квантовая физика. Тема № 5 Деление ядер урана. Цепная реакция. Ядерный реактор. Термоядерные реакции
Деление ядер урана. Цепная реакция. Ядерный реактор. Термоядерные реакции Динамика
Динамика Никель-кадмиевые аккумуляторные батареи
Никель-кадмиевые аккумуляторные батареи Электродинамика - раздел физики, которая изучает электрические и магнитные поля
Электродинамика - раздел физики, которая изучает электрические и магнитные поля Игра по физике Тайна черных ящиков для учащихся 10-11 классов
Игра по физике Тайна черных ящиков для учащихся 10-11 классов Примесные полупроводники
Примесные полупроводники Электропроводность биологических тканей на постоянном токе
Электропроводность биологических тканей на постоянном токе Агрегатные состояния вещества. Урок в 7 классе
Агрегатные состояния вещества. Урок в 7 классе Влажность воздуха
Влажность воздуха Ремонт автомобилей. Нормирование шлифовальных работ. (Тема 5.2.4)
Ремонт автомобилей. Нормирование шлифовальных работ. (Тема 5.2.4) Двигатель внутреннего сгорания
Двигатель внутреннего сгорания Энергия. Тест. 10 класс
Энергия. Тест. 10 класс Электрические цепи в режиме постоянного тока и гармонических воздействий
Электрические цепи в режиме постоянного тока и гармонических воздействий 11kl-06_02_24_Kvantovaya_fizika_Fotoeffekt
11kl-06_02_24_Kvantovaya_fizika_Fotoeffekt Проект Экзофиз
Проект Экзофиз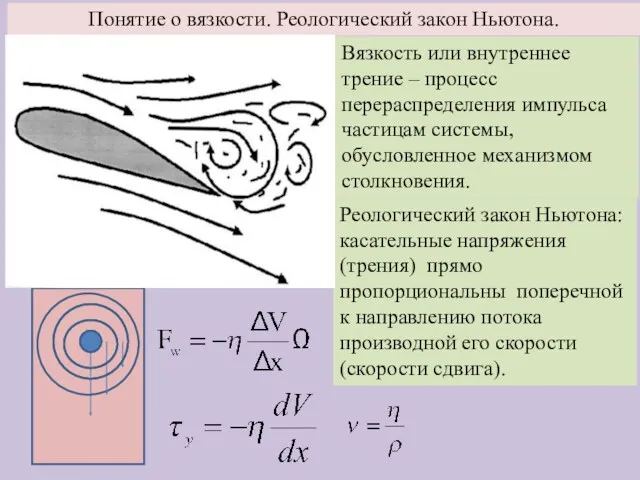 Понятие о вязкости. Реологический закон Ньютона
Понятие о вязкости. Реологический закон Ньютона Виды теплообмена. Примеры теплообмена в природе и технике
Виды теплообмена. Примеры теплообмена в природе и технике Презентация к уроку физики 11 класса по теме Обобщение и закрепление знаний, умений и навыков по теме Оптика.
Презентация к уроку физики 11 класса по теме Обобщение и закрепление знаний, умений и навыков по теме Оптика.