Содержание
- 2. Геостатистика це розділ статистики, що вивчає технології та методи для аналізу, оброблення і подання просторово-розподіленої (та/або
- 3. Практичні завдання геостатистики оцінка значення в точці, де спостереження не проводились; оцінювання похибки інтерполяції та врахування
- 4. Основні етапи геостатистичного аналізу Статистичний аналіз даних - дослідження даних (визначення статистичних параметрів, перевірка на нормальність,
- 5. Концепція геостатистичного аналізу
- 6. Варіаграма - це статистичний момент другого порядку випадкової функції Z(x), що застосовують для кількісного опису просторової
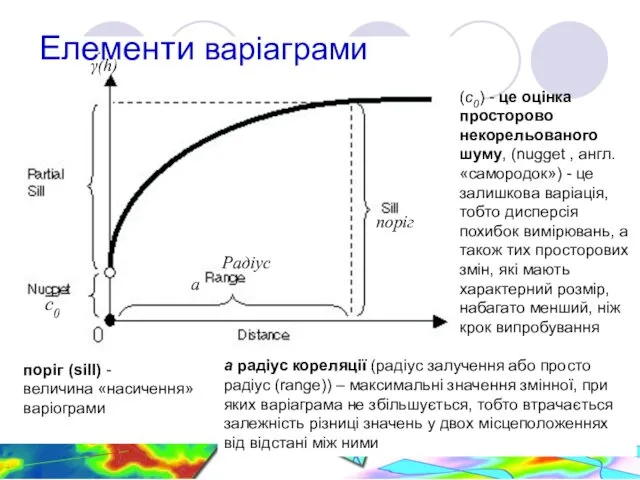
- 7. Елементи варіаграми (с0) - це оцінка просторово некорельованого шуму, (nugget , англ. «самородок») - це залишкова
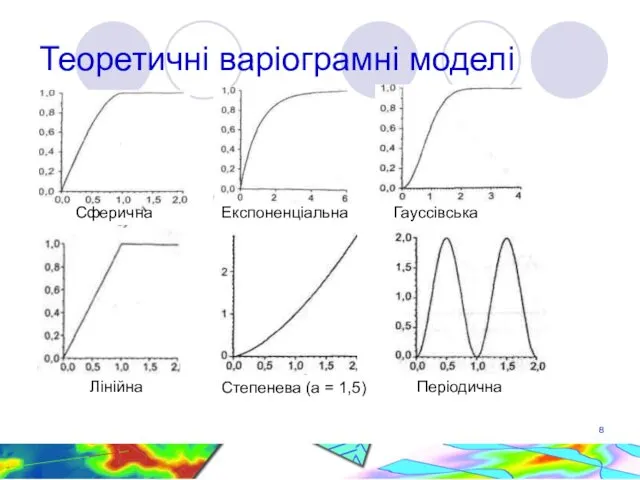
- 8. Теоретичні варіограмні моделі
- 9. Просторова інтерполяція Інтерполяція — спосіб знаходження проміжних значень величини за наявним дискретним набором відомих значень Завданням
- 10. Просторова інтерполяція Методи інтерполяції Глобальні Локальні детерміновані стохастичні - класифікації з використанням зовнішньої інформації; - поліноміальна
- 11. Просторова інтерполяція
- 12. Обернена зважена відстань Inverse Distance Method (IDM) полягає в тому, що значення атрибута z в довільній
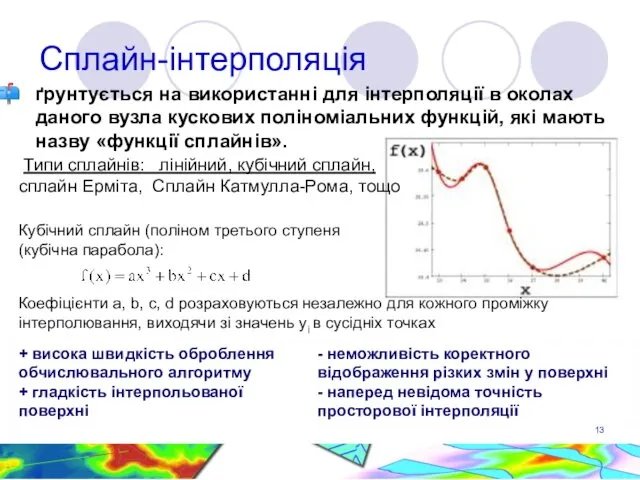
- 13. Сплайн-інтерполяція ґрунтується на використанні для інтерполяції в околах даного вузла кускових поліноміальних функцій, які мають назву
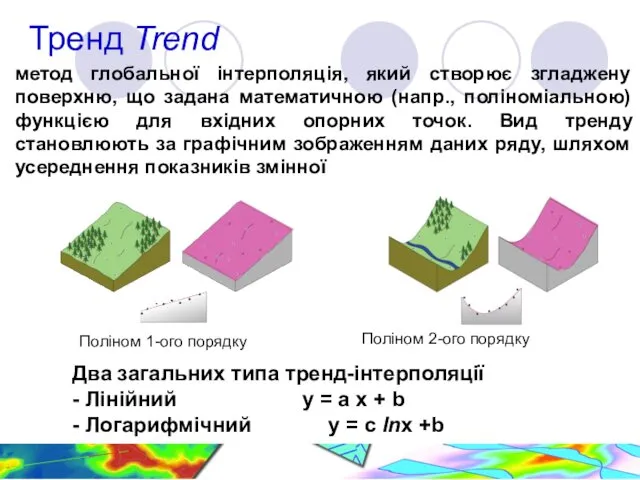
- 14. Тренд Trend Поліном 2-ого порядку Два загальних типа тренд-інтерполяції - Лінійний y = a x +
- 15. Крігінг / Kriging це метод находження кращої незміщеною лінійної оцінки (тобто найменшої дисперсії) значень точок Dr
- 16. Крігінг / Kriging Випадкова функція V (x) зазвичай розкладається на дві компоненти: детерміністичний тренд m(x) та
- 17. Крігінг / Kriging Умови: 1) Незміщені оцінки V*(x) в точці x (середнє значення похибки оцінювання дорівнює
- 18. Крігінг / Kriging
- 19. Вибір методу інтерполяції Отримана вибірка значень підлягає статистичній обробці, при перевищенні визначеного дослідником рівня наближення в
- 20. Геостатистика Багатофакторний аналіз
- 21. Багатофакторний аналіз предметом багатофакторного аналізу є дослідження впливу декількох різноманітних показників (факторів) на об'єкт дослідження з
- 22. Кореляція ( від лат. correlatio - співвідношення) – це статистична залежність між випадковими величинами, що носить
- 23. Регресія Основне завдання регресійного аналізу є встановлення форми і вивчення залежності змінних Р. дозволяє за величиною
- 24. Просторова регресія Географічна зважена регресія (ГВР) (Geographically Weighted Regression) - один з декількох методів просторового регресійного
- 25. Просторова регресія Методи обчислювання вагових коефіцієнтів - метод адміністративно-територіального поділу; - метод рухомого фіксованого вікна; -
- 26. Просторова автокореляція (autocorrelation) це статистична міра, що описує, як змінюється одна властивість з залежності від інших
- 27. Просторова автокореляція Загальний вид просторової залежності : де E – математичне очікування події yi, yj. В
- 28. Просторова матриця ваг - відображає припущення, що розподіл певних явищ та об’єктів (або їх інтенсивність) залежить
- 29. Приклад матриці ваг Нормалізація матриці ваг по рядку
- 30. Показники автокореляції Глобальні показники оцінюють загальну структуру та тренд даних та є найбільш ефективними, коли просторові
- 31. Діаграма Морана І І – кут нахилу в регресії: Wx=c+lx+Ɛ
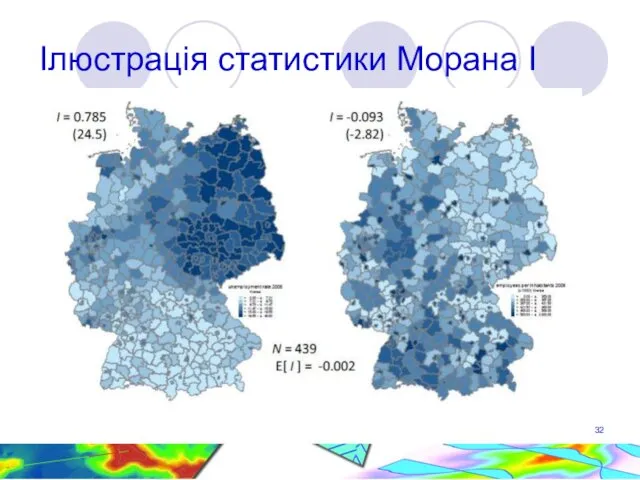
- 32. Ілюстрація статистики Морана І
- 33. Інструменти ArcGIS Geoprocessing » Tool reference » Spatial Statistics toolbox»Modeling Spatial Relationships toolset
- 34. Література Каневский М.Ф., Демьянов В.В., Савельева Е.А., Чернов С.Ю., Тимонин В.А. Элементарное введение в геостатистику серия
- 36. Скачать презентацию




























 Марийский народ
Марийский народ Рудольф Челлен и его вклад в геополитическую концепцию
Рудольф Челлен и его вклад в геополитическую концепцию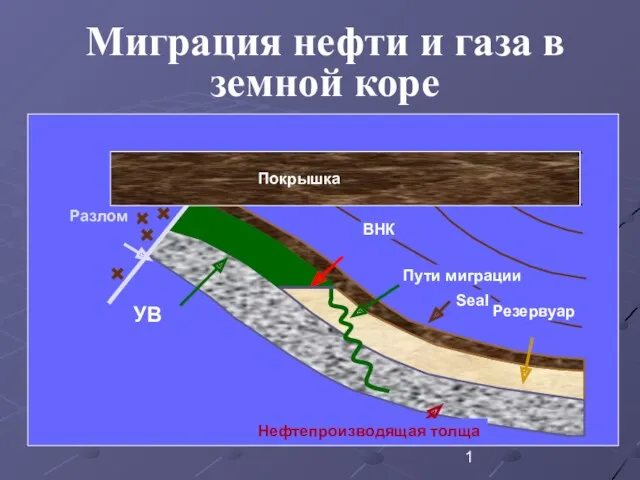 Миграция нефти и газа в земной коре
Миграция нефти и газа в земной коре Население Африки
Население Африки Объекты культурного наследия Австралии и Океании
Объекты культурного наследия Австралии и Океании Республика Хорватия
Республика Хорватия Океаны (7 класс)
Океаны (7 класс) Природные зоны планеты
Природные зоны планеты Животный и растительный мир природных зон России
Животный и растительный мир природных зон России Атмосфера. 6 класс
Атмосфера. 6 класс Мексика (Мексиканские Соединенные Штаты)
Мексика (Мексиканские Соединенные Штаты) Бельгия
Бельгия Климат и климатические ресурсы
Климат и климатические ресурсы План и географическая карта
План и географическая карта Землетрясения и вулканы
Землетрясения и вулканы Внутренние воды. Реки Донецкого края
Внутренние воды. Реки Донецкого края Складчатые формы залегания слоев
Складчатые формы залегания слоев Біосфера. Поняття біосфера
Біосфера. Поняття біосфера Республика Молдова
Республика Молдова Вулканы. ( 3 класс)
Вулканы. ( 3 класс) Физико-географическое положение и исследования Евразии
Физико-географическое положение и исследования Евразии Путешествие на остров Ява
Путешествие на остров Ява Латинская Америка
Латинская Америка Зона Арктических пустынь
Зона Арктических пустынь Значение природных условий в жизни человека. 2 класс
Значение природных условий в жизни человека. 2 класс Північна Америка. Геологічна будова
Північна Америка. Геологічна будова Геоморфологічна будова. Закорномірності поширення основних форм і типів рельєфу
Геоморфологічна будова. Закорномірності поширення основних форм і типів рельєфу Своя игра
Своя игра