Содержание
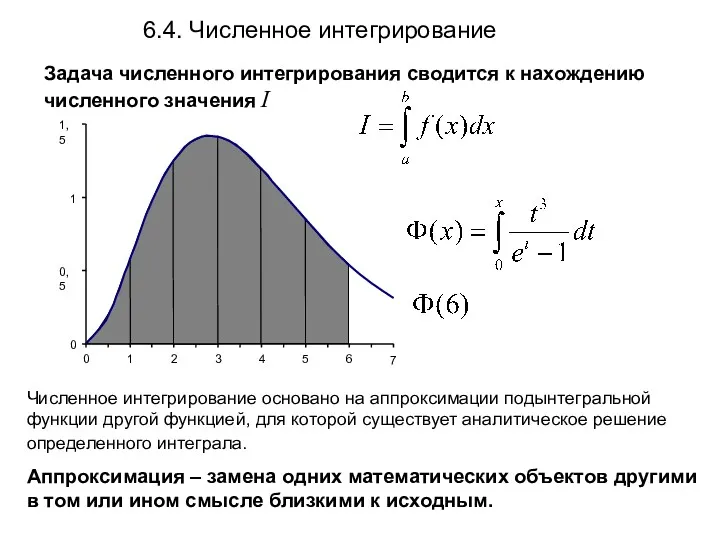
- 2. Задача численного интегрирования сводится к нахождению численного значения I 6.4. Численное интегрирование Численное интегрирование основано на
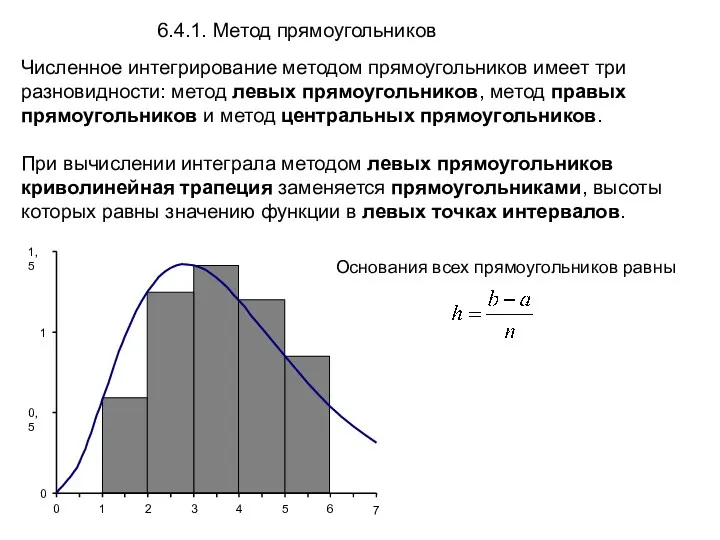
- 3. Численное интегрирование методом прямоугольников имеет три разновидности: метод левых прямоугольников, метод правых прямоугольников и метод центральных
- 4. Метод левых прямоугольников Формула вычисления интеграла методом левых прямоугольников
- 5. Пример. Вычислить интеграл методом левых прямоугольников Метод левых прямоугольников
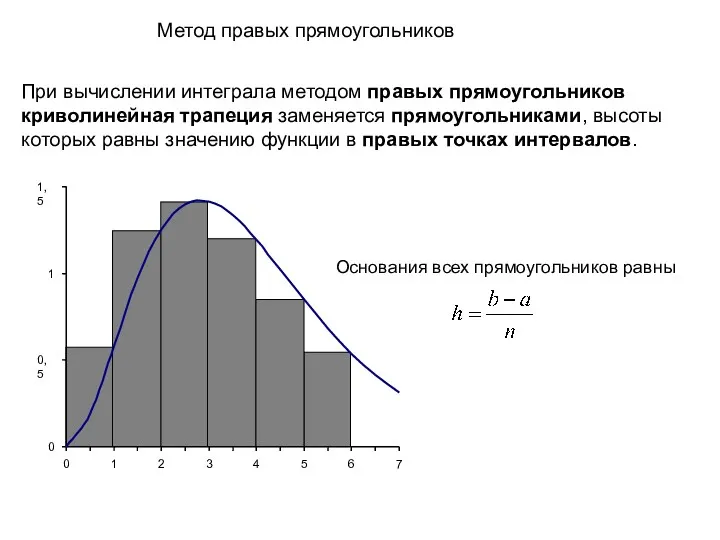
- 6. При вычислении интеграла методом правых прямоугольников криволинейная трапеция заменяется прямоугольниками, высоты которых равны значению функции в
- 7. Метод правых прямоугольников Формула вычисления интеграла методом правых прямоугольников
- 8. Пример. Вычислить интеграл методом правых прямоугольников Метод правых прямоугольников
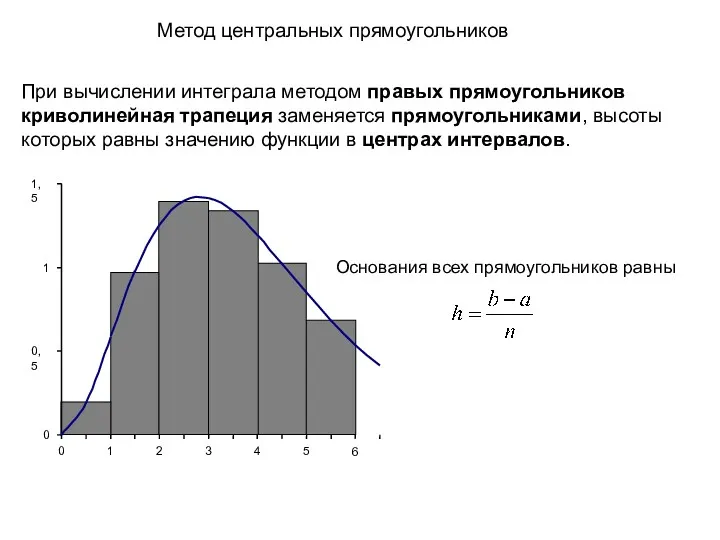
- 9. При вычислении интеграла методом правых прямоугольников криволинейная трапеция заменяется прямоугольниками, высоты которых равны значению функции в
- 10. Метод центральных прямоугольников Формула вычисления интеграла методом центральных прямоугольников
- 11. Пример. Вычислить интеграл методом центральных прямоугольников Метод правых прямоугольников
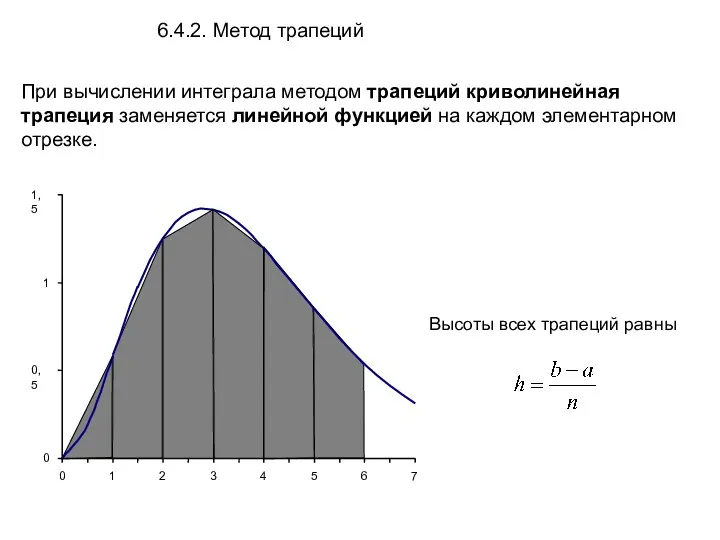
- 12. При вычислении интеграла методом трапеций криволинейная трапеция заменяется линейной функцией на каждом элементарном отрезке. 6.4.2. Метод
- 13. Метод трапеций Формула вычисления интеграла методом трапеций
- 14. Пример. Вычислить интеграл методом трапеций Метод трапеций
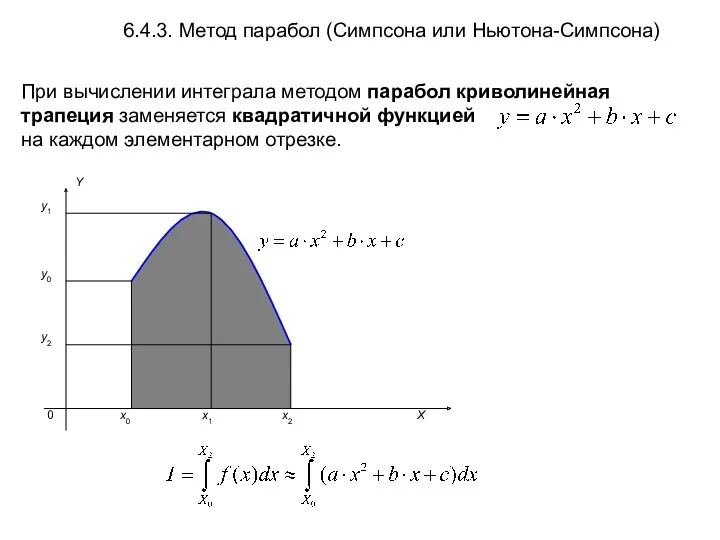
- 15. При вычислении интеграла методом парабол криволинейная трапеция заменяется квадратичной функцией на каждом элементарном отрезке. 6.4.3. Метод
- 16. Метод парабол
- 17. Метод парабол
- 18. Коэффициенты параболы определяются из условия прохождения параболы через три точки
- 21. Метод парабол Формула вычисления интеграла методом парабол (n кратно 2)
- 22. Пример. Вычислить интеграл методом парабол Метод парабол
- 23. При вычислении интеграла методом Симпсона 3/8 криволинейная трапеция на каждом элементарном отрезке заменяется полиномом третьей степени
- 24. Пример. Вычислить интеграл методом Симпсона 3/8 Метод парабол
- 25. При вычислении интеграла методом Буля криволинейная трапеция на каждом элементарном отрезке заменяется полиномом четвертой степени 6.4.5.
- 26. Степенью точности называют такое целое число n, что для всех полиномов Pi(x) степени i ≤ n
- 27. 6.4.6. Сравнение различных методов по точности приближения
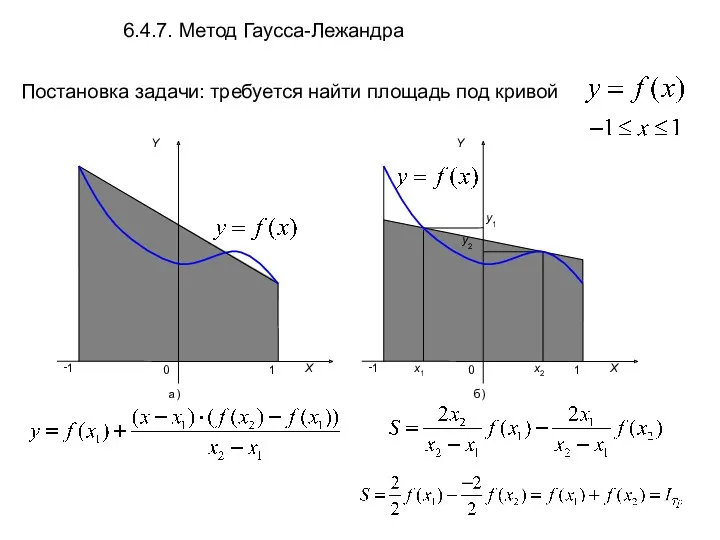
- 28. Постановка задачи: требуется найти площадь под кривой 6.4.7. Метод Гаусса-Лежандра
- 29. Согласно методу Гаусса-Лежандра приближенное значение интеграла определяется с помощью весового суммирования значений функции в двух точках
- 32. Пример. Вычислить интеграл методом Гаусса-Лежандра по 2 точкам Метод Гаусса-Лежандра
- 33. Если требуется вычислить значение интеграла на интервале [a; b], то требуется выполнить замену переменной Метод Гаусса-Лежандра
- 34. Если требуется вычислить значение интеграла на интервале [a; b], то требуется выполнить замену переменной Метод Гаусса-Лежандра
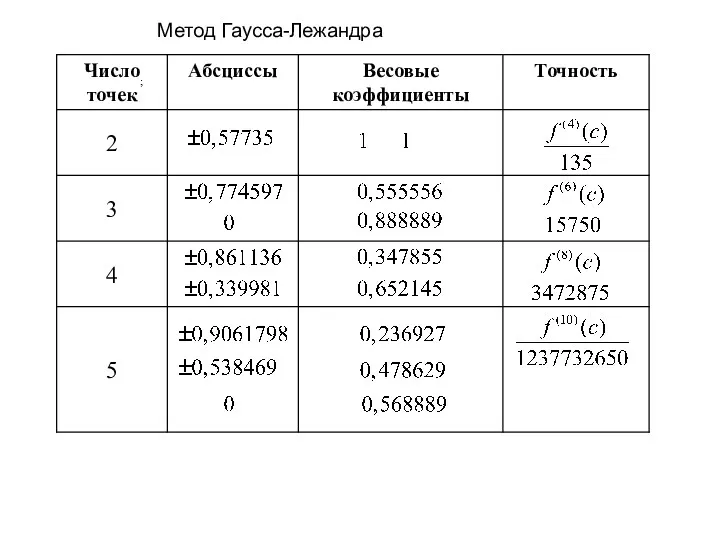
- 35. При вычислении интеграла методом Гаусса-Лежандра по трем точкам приближенное значение определяется по формуле Значения абсцисс x1,
- 36. Метод Гаусса-Лежандра ;
- 37. Николас Константин Метрополис, Станислав Мартин Улам – авторы статьи «Метод Монте-Карло» (1950 г.) 6.4.8. Метод Монте-Карло
- 38. u – случайная величина, равномерно распределенная на интервале [a; b] 6.4.8. Метод Монте-Карло – плотность распределения
- 39. 6.4.8. Метод Монте-Карло Формула вычисления интеграла простейшим методом Монте-Карло
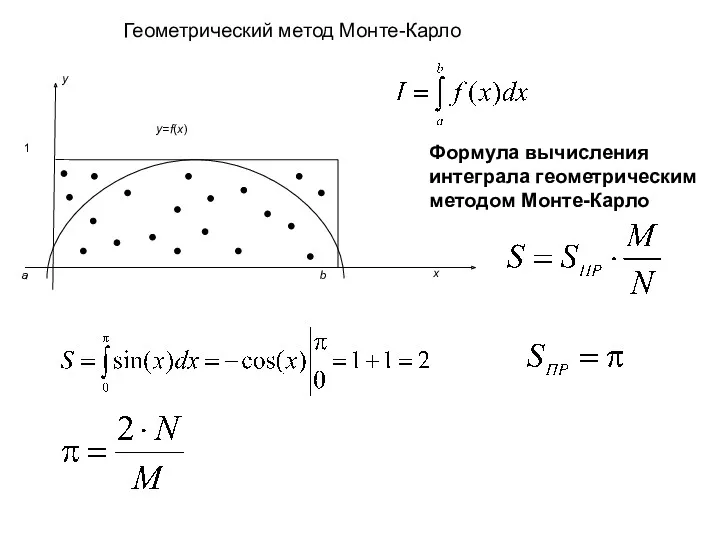
- 40. Геометрический метод Монте-Карло Формула вычисления интеграла геометрическим методом Монте-Карло
- 42. Скачать презентацию











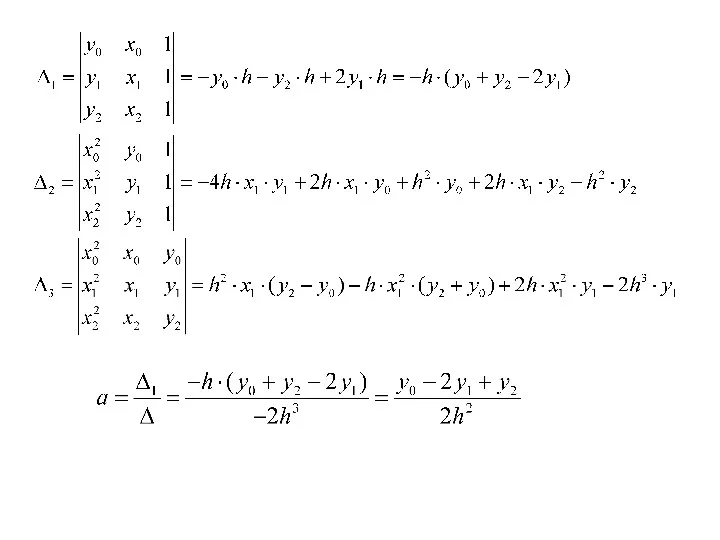
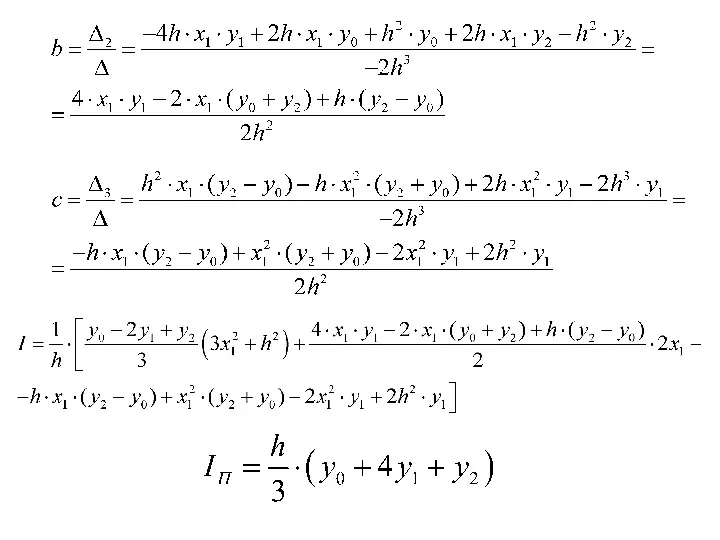








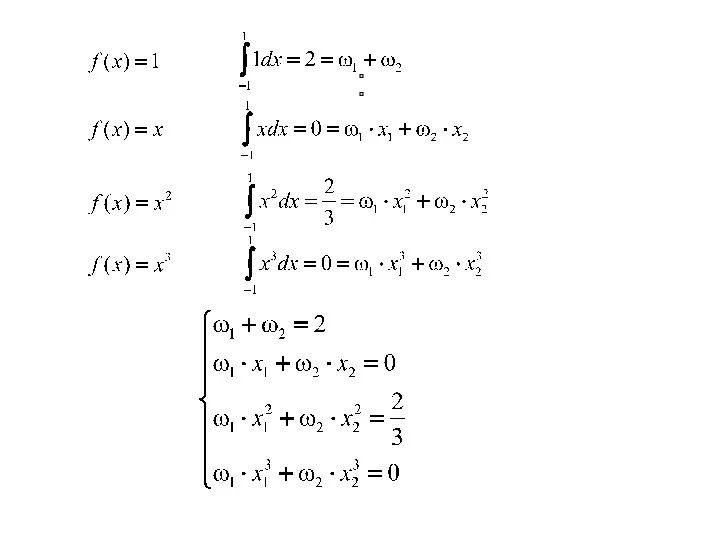
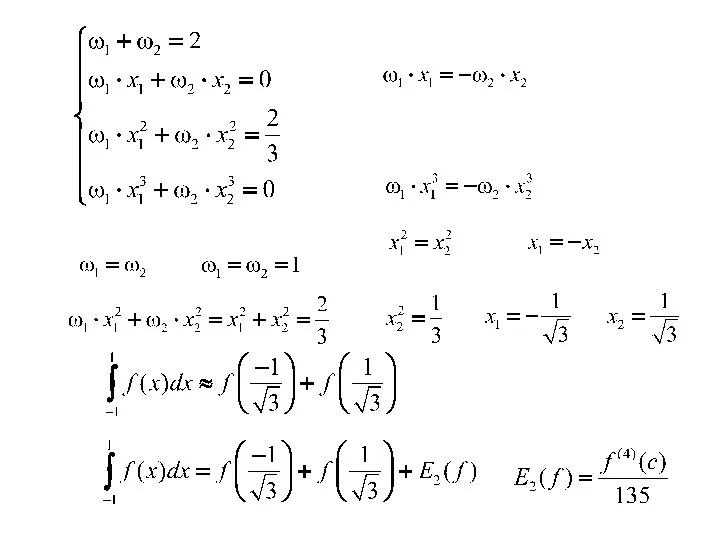

![Если требуется вычислить значение интеграла на интервале [a; b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/233430/slide-32.jpg)
![Если требуется вычислить значение интеграла на интервале [a; b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/233430/slide-33.jpg)


![u – случайная величина, равномерно распределенная на интервале [a; b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/233430/slide-37.jpg)

 Однострочные функции
Однострочные функции Исполнитель Робот. Вспомогательные алгоритмы
Исполнитель Робот. Вспомогательные алгоритмы Разработка интернет-магазина с применением шаблона проектирования MODEL-VIEW-CONTROLLER
Разработка интернет-магазина с применением шаблона проектирования MODEL-VIEW-CONTROLLER Построение графиков в табличном процессоре. 9 класс
Построение графиков в табличном процессоре. 9 класс Справочно-библиографическое обслуживание в современной общедоступной библиотеке: технологии и ресурсы
Справочно-библиографическое обслуживание в современной общедоступной библиотеке: технологии и ресурсы Программирование на языке Паскаль. (§ 54 - § 61)
Программирование на языке Паскаль. (§ 54 - § 61) Информационная безопасность
Информационная безопасность Структура информационно-библиотечного центра
Структура информационно-библиотечного центра Екі өлшемді массив
Екі өлшемді массив Лингвистические парадоксы. Удивительный мир научных книг - 2018
Лингвистические парадоксы. Удивительный мир научных книг - 2018 Программирование на языке Java. Алгоритмы и программы
Программирование на языке Java. Алгоритмы и программы Роль модульных сеток всех видов в создании унифицированной схемы верстки всей печатной продукции корпорации
Роль модульных сеток всех видов в создании унифицированной схемы верстки всей печатной продукции корпорации Правовая защита коммерческой тайны. Сведения, составляющие коммерческую тайну (ОПОИБ, лекция 4.1)
Правовая защита коммерческой тайны. Сведения, составляющие коммерческую тайну (ОПОИБ, лекция 4.1) Коллекция автографов известных ученых на книгах
Коллекция автографов известных ученых на книгах Разработки уроков по информатике и ИКТ
Разработки уроков по информатике и ИКТ Оператор цикла с параметром
Оператор цикла с параметром Основные этапы разработки ПО. Жизненный цикл ПО. Лекция №1
Основные этапы разработки ПО. Жизненный цикл ПО. Лекция №1 S.O.L.I.D. Принципы на практике
S.O.L.I.D. Принципы на практике Тестирование программного обеспечения
Тестирование программного обеспечения Компьютерные сети
Компьютерные сети Теории медиаобразования
Теории медиаобразования Технология распознавания лиц – будущее настало?
Технология распознавания лиц – будущее настало? Quickly SlidesCarnival
Quickly SlidesCarnival Базы данных. Система управления базами данных
Базы данных. Система управления базами данных Основы обработки и передачи информации в АСУ
Основы обработки и передачи информации в АСУ презентация для урока в 10 классе по учебнику Семакина Программирование линейных алгоритмов, Практическая работа №8
презентация для урока в 10 классе по учебнику Семакина Программирование линейных алгоритмов, Практическая работа №8 Представление архитектуры ИС
Представление архитектуры ИС Составление сметной документации ООО НПП АВС-Н
Составление сметной документации ООО НПП АВС-Н