Содержание
- 2. * Data Mining: Concepts and Techniques Chapter 8. Cluster Analysis What is Cluster Analysis? Types of
- 3. What is Cluster Analysis? Cluster: a collection of data objects Similar to one another within the
- 4. * Data Mining: Concepts and Techniques General Applications of Clustering Pattern Recognition Spatial Data Analysis create
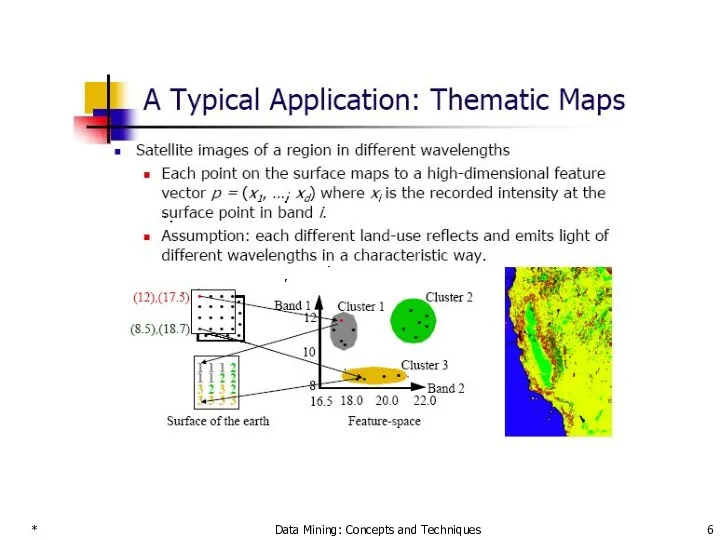
- 5. * Data Mining: Concepts and Techniques Examples of Clustering Applications Marketing: Help marketers discover distinct groups
- 6. * Data Mining: Concepts and Techniques
- 7. * Data Mining: Concepts and Techniques
- 8. * Data Mining: Concepts and Techniques
- 9. * Data Mining: Concepts and Techniques What Is Good Clustering? A good clustering method will produce
- 10. * Data Mining: Concepts and Techniques Requirements of Clustering in Data Mining Scalability Ability to deal
- 11. * Data Mining: Concepts and Techniques Chapter 8. Cluster Analysis What is Cluster Analysis? Types of
- 12. * Data Mining: Concepts and Techniques Data Structures Data matrix (two modes) Dissimilarity matrix (one mode)
- 13. * Data Mining: Concepts and Techniques Measure the Quality of Clustering Dissimilarity/Similarity metric: Similarity is expressed
- 14. * Data Mining: Concepts and Techniques
- 15. * Data Mining: Concepts and Techniques
- 16. * Data Mining: Concepts and Techniques
- 17. * Data Mining: Concepts and Techniques Type of data in clustering analysis Interval-scaled variables: Binary variables:
- 18. * Data Mining: Concepts and Techniques Interval-valued variables Standardize data Calculate the mean absolute deviation: where
- 19. * Data Mining: Concepts and Techniques Binary Variables A contingency table for binary data Simple matching
- 20. * Data Mining: Concepts and Techniques Binary Variables Association coefficient Yule: Q(i,j)= ad-bc/ ad+bc Rassel and
- 21. * Data Mining: Concepts and Techniques Dissimilarity between Binary Variables Example gender is a symmetric attribute
- 22. * Data Mining: Concepts and Techniques Nominal Variables A generalization of the binary variable in that
- 23. * Data Mining: Concepts and Techniques Ordinal Variables An ordinal variable can be discrete or continuous
- 24. * Data Mining: Concepts and Techniques Ratio-Scaled Variables Ratio-scaled variable: a positive measurement on a nonlinear
- 25. * Data Mining: Concepts and Techniques Variables of Mixed Types A database may contain all the
- 26. * Data Mining: Concepts and Techniques Chapter 8. Cluster Analysis What is Cluster Analysis? Types of
- 27. * Data Mining: Concepts and Techniques Major Clustering Approaches Partitioning algorithms: Construct various partitions and then
- 28. * Data Mining: Concepts and Techniques Chapter 8. Cluster Analysis What is Cluster Analysis? Types of
- 29. * Data Mining: Concepts and Techniques Partitioning Algorithms: Basic Concept Partitioning method: Construct a partition of
- 30. * Data Mining: Concepts and Techniques
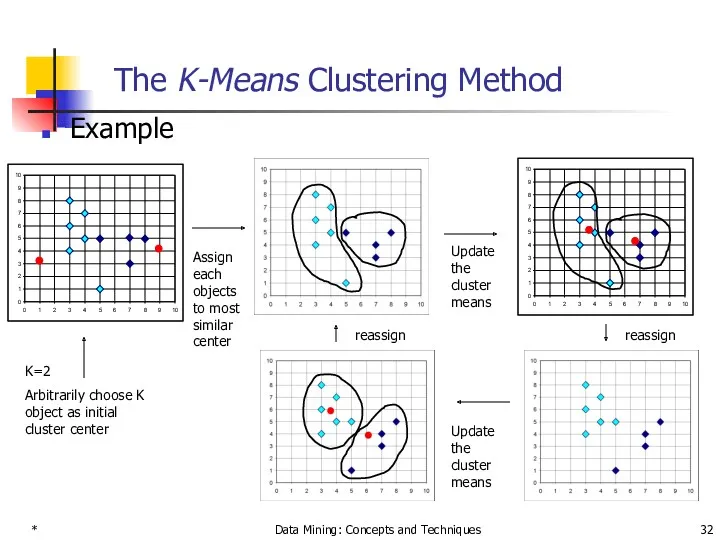
- 31. * Data Mining: Concepts and Techniques The K-Means Clustering Method Given k, the k-means algorithm is
- 32. * Data Mining: Concepts and Techniques The K-Means Clustering Method Example 0 1 2 3 4
- 33. * Data Mining: Concepts and Techniques Comments on the K-Means Method Strength: Relatively efficient: O(tkn), where
- 34. * Data Mining: Concepts and Techniques Variations of the K-Means Method A few variants of the
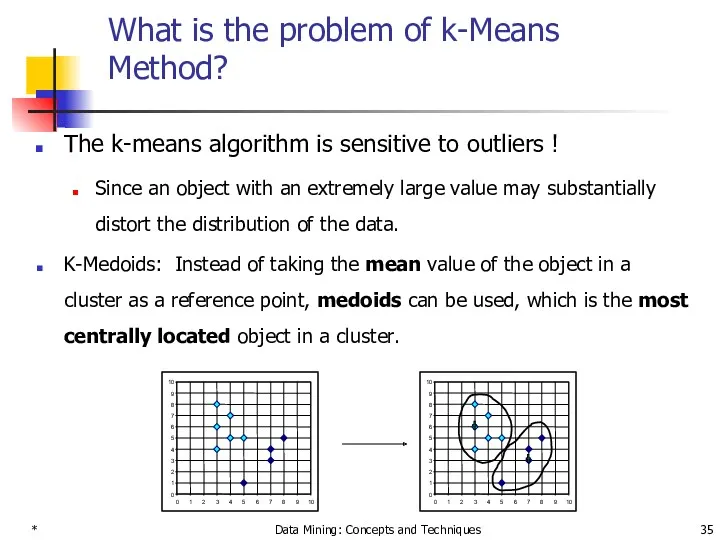
- 35. * Data Mining: Concepts and Techniques What is the problem of k-Means Method? The k-means algorithm
- 36. * Data Mining: Concepts and Techniques
- 37. * Data Mining: Concepts and Techniques
- 38. * Data Mining: Concepts and Techniques
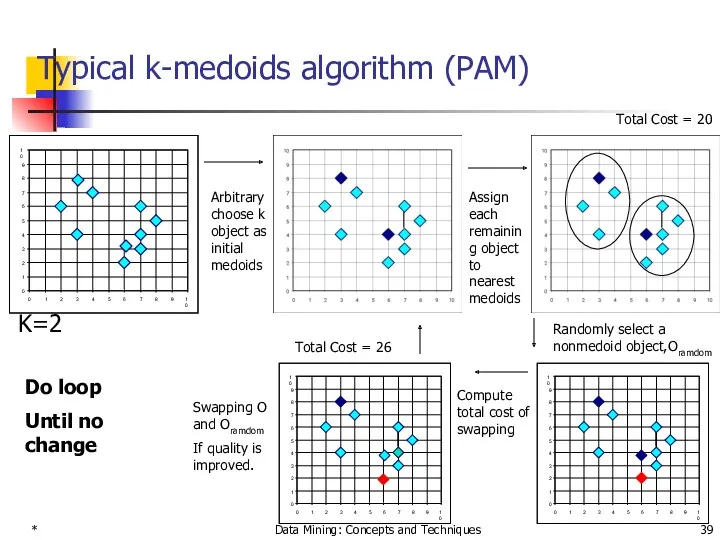
- 39. * Data Mining: Concepts and Techniques Typical k-medoids algorithm (PAM) Total Cost = 20 0 1
- 40. * Data Mining: Concepts and Techniques What is the problem with PAM? Pam is more robust
- 41. * Data Mining: Concepts and Techniques
- 42. * Data Mining: Concepts and Techniques CLARA (Clustering Large Applications) (1990) CLARA (Kaufmann and Rousseeuw in
- 43. * Data Mining: Concepts and Techniques CLARANS (“Randomized” CLARA) (1994) CLARANS (A Clustering Algorithm based on
- 44. * Data Mining: Concepts and Techniques
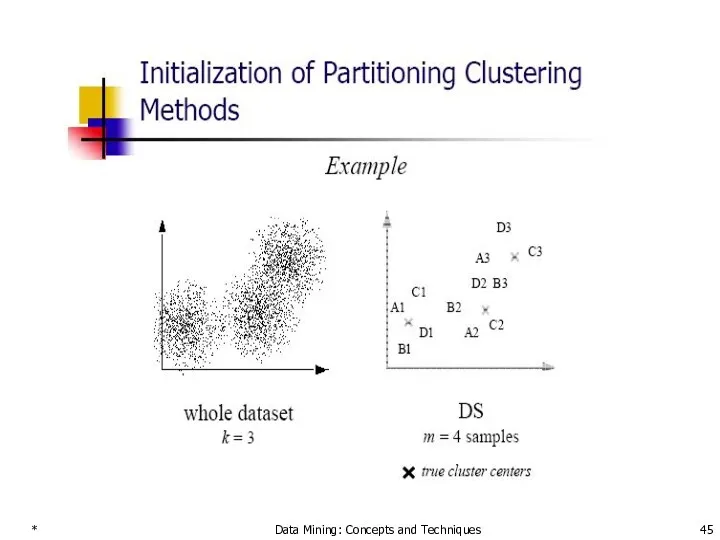
- 45. * Data Mining: Concepts and Techniques
- 46. * Data Mining: Concepts and Techniques
- 47. * Data Mining: Concepts and Techniques
- 48. * Data Mining: Concepts and Techniques Chapter 8. Cluster Analysis What is Cluster Analysis? Types of
- 49. * Data Mining: Concepts and Techniques
- 50. * Data Mining: Concepts and Techniques
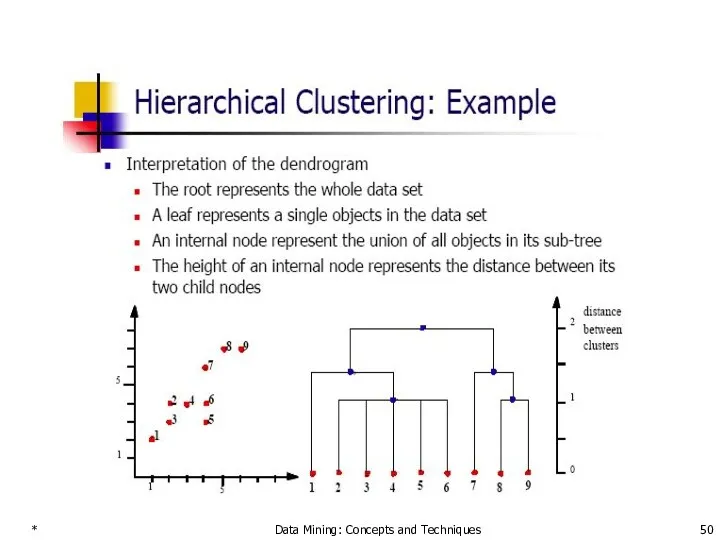
- 51. * Data Mining: Concepts and Techniques A Dendrogram Shows How the Clusters are Merged Hierarchically Decompose
- 52. * Data Mining: Concepts and Techniques A Dendrogram Algorithm for Binary variables 1. To estimate similarity
- 53. * Data Mining: Concepts and Techniques Example for binary variables ecoli1 0 1 1 1 0
- 54. * Data Mining: Concepts and Techniques ecoli2 ecoli3 J23=14/16=0.875 2. Incedence matrix ecoli1 ecoli2 ecoli3 ecoli1
- 55. * Data Mining: Concepts and Techniques A Dendrogram Algorithm for Numerical variables 1. To estimate similarity
- 56. * Data Mining: Concepts and Techniques
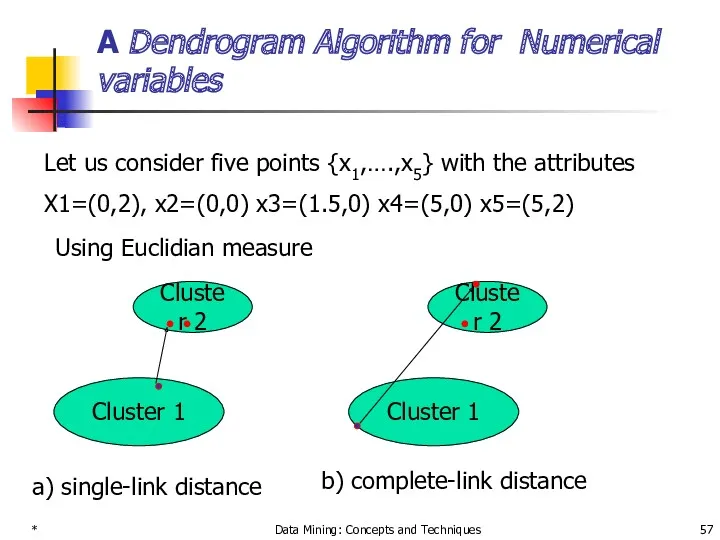
- 57. * Data Mining: Concepts and Techniques A Dendrogram Algorithm for Numerical variables Let us consider five
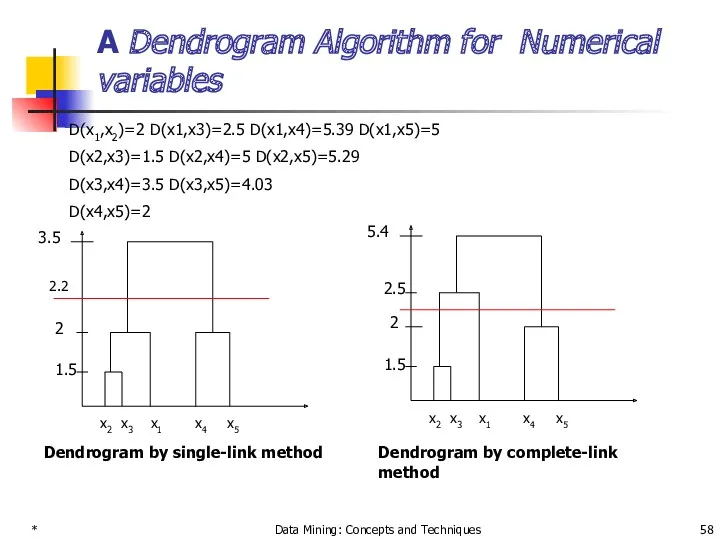
- 58. * Data Mining: Concepts and Techniques A Dendrogram Algorithm for Numerical variables D(x1,x2)=2 D(x1,x3)=2.5 D(x1,x4)=5.39 D(x1,x5)=5
- 59. * Data Mining: Concepts and Techniques Hierarchical Clustering Use distance matrix as clustering criteria. This method
- 60. * Data Mining: Concepts and Techniques
- 61. * Data Mining: Concepts and Techniques AGNES (Agglomerative Nesting) Introduced in Kaufmann and Rousseeuw (1990) Implemented
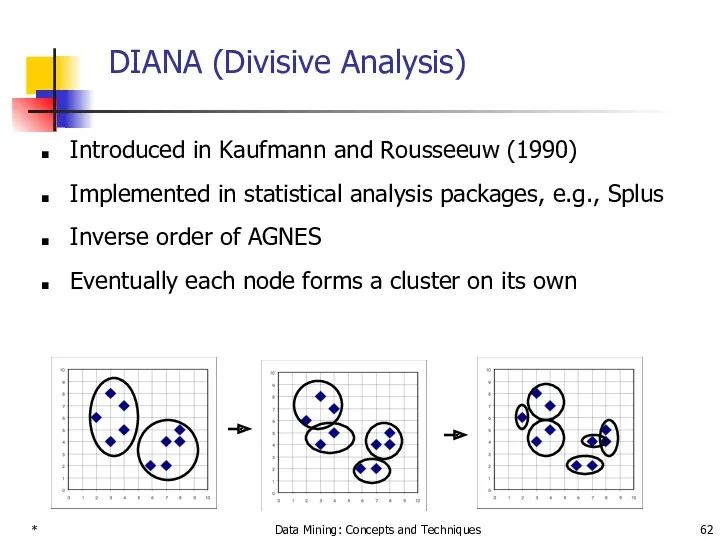
- 62. * Data Mining: Concepts and Techniques DIANA (Divisive Analysis) Introduced in Kaufmann and Rousseeuw (1990) Implemented
- 63. * Data Mining: Concepts and Techniques More on Hierarchical Clustering Methods Major weakness of agglomerative clustering
- 64. * Data Mining: Concepts and Techniques BIRCH (1996) Birch: Balanced Iterative Reducing and Clustering using Hierarchies,
- 65. * Data Mining: Concepts and Techniques Clustering Feature Vector CF = (5, (16,30),(54,190)) (3,4) (2,6) (4,5)
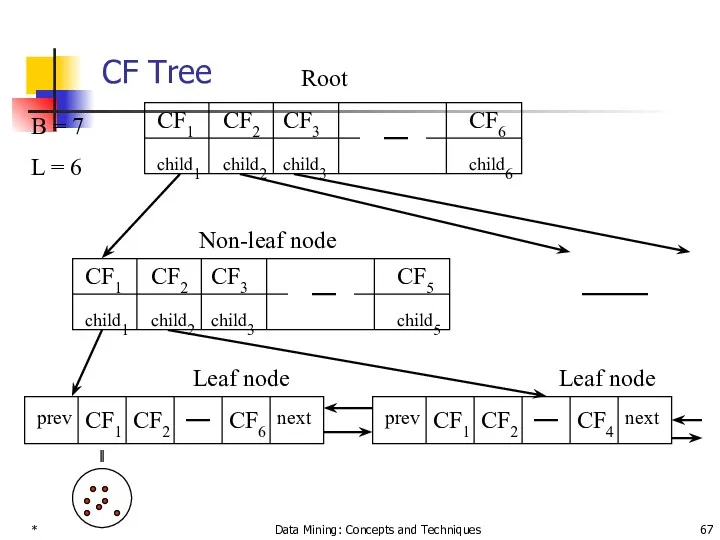
- 66. * Data Mining: Concepts and Techniques CF-Tree in BIRCH Clustering feature: summary of the statistics for
- 67. * Data Mining: Concepts and Techniques CF Tree CF1 child1 CF3 child3 CF2 child2 CF5 child5
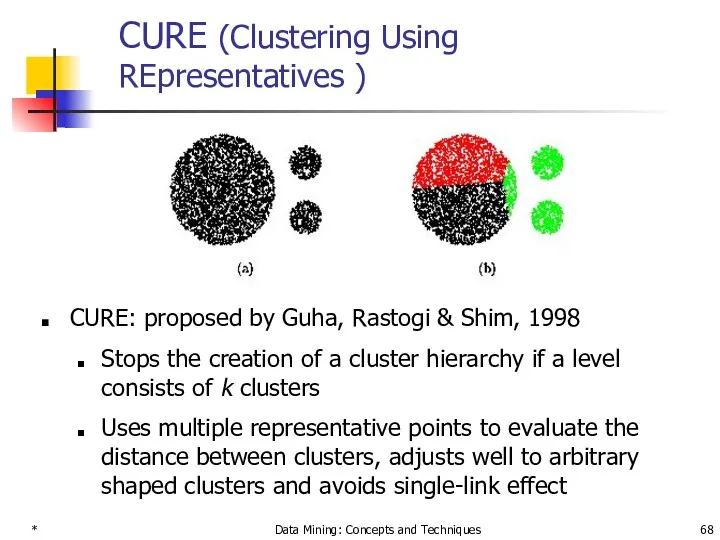
- 68. * Data Mining: Concepts and Techniques CURE (Clustering Using REpresentatives ) CURE: proposed by Guha, Rastogi
- 69. * Data Mining: Concepts and Techniques Drawbacks of Distance-Based Method Drawbacks of square-error based clustering method
- 70. * Data Mining: Concepts and Techniques Cure: The Algorithm Draw random sample s. Partition sample to
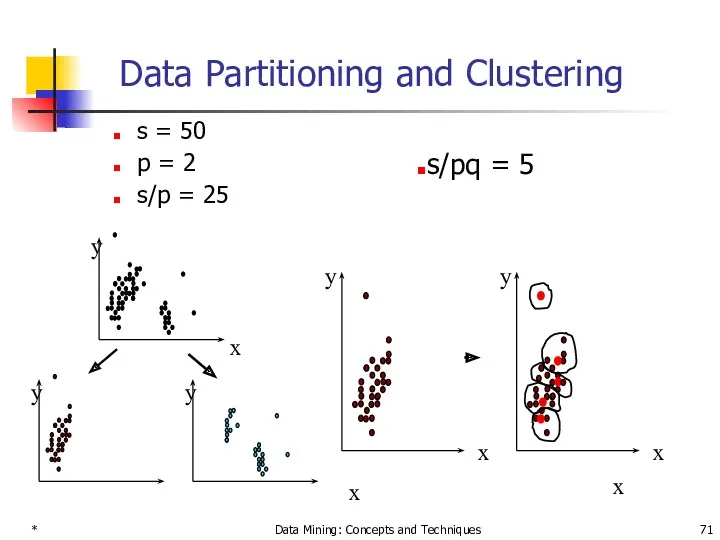
- 71. * Data Mining: Concepts and Techniques Data Partitioning and Clustering s = 50 p = 2
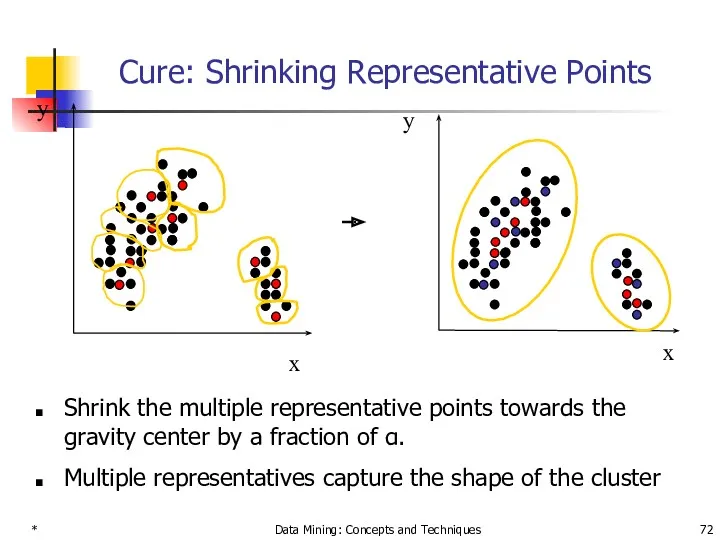
- 72. * Data Mining: Concepts and Techniques Cure: Shrinking Representative Points Shrink the multiple representative points towards
- 73. * Data Mining: Concepts and Techniques Clustering Categorical Data: ROCK ROCK: Robust Clustering using linKs, by
- 74. * Data Mining: Concepts and Techniques Rock: Algorithm Links: The number of common neighbors for the
- 75. * Data Mining: Concepts and Techniques CHAMELEON (Hierarchical clustering using dynamic modeling) CHAMELEON: by G. Karypis,
- 76. * Data Mining: Concepts and Techniques Overall Framework of CHAMELEON Construct Sparse Graph Partition the Graph
- 77. * Data Mining: Concepts and Techniques Chapter 8. Cluster Analysis What is Cluster Analysis? Types of
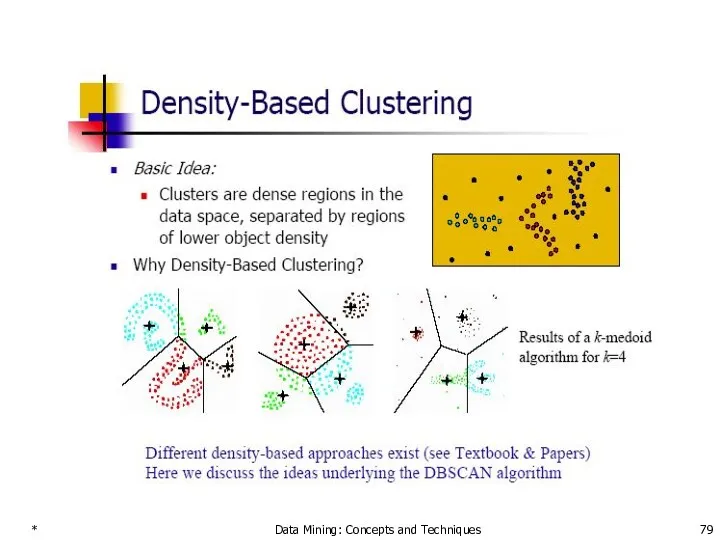
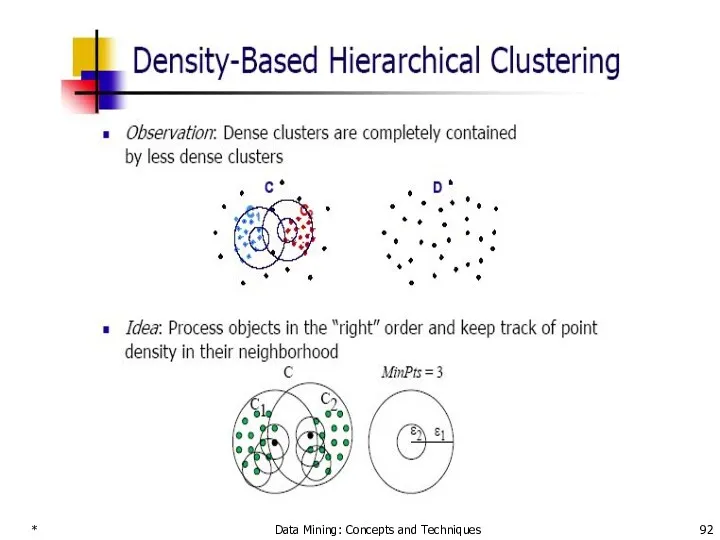
- 78. * Data Mining: Concepts and Techniques Density-Based Clustering Methods Clustering based on density (local cluster criterion),
- 79. * Data Mining: Concepts and Techniques
- 80. * Data Mining: Concepts and Techniques
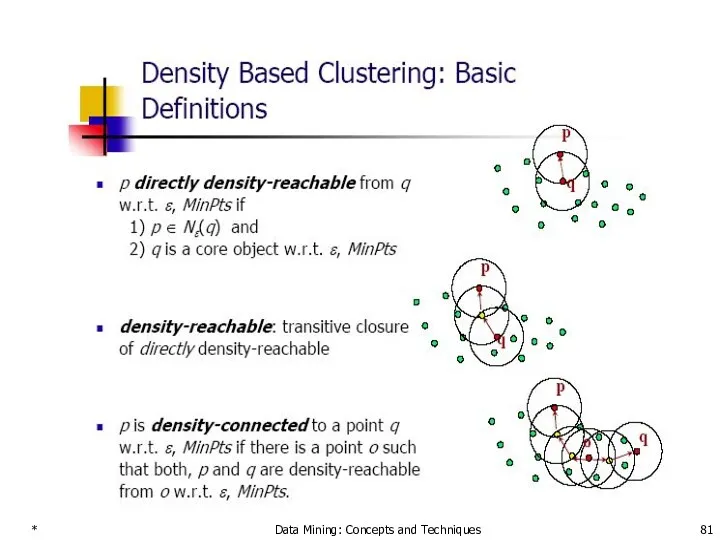
- 81. * Data Mining: Concepts and Techniques
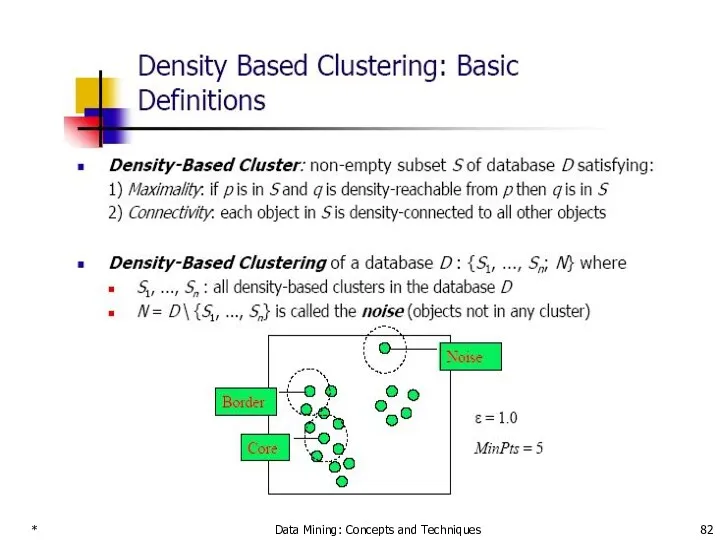
- 82. * Data Mining: Concepts and Techniques
- 83. * Data Mining: Concepts and Techniques
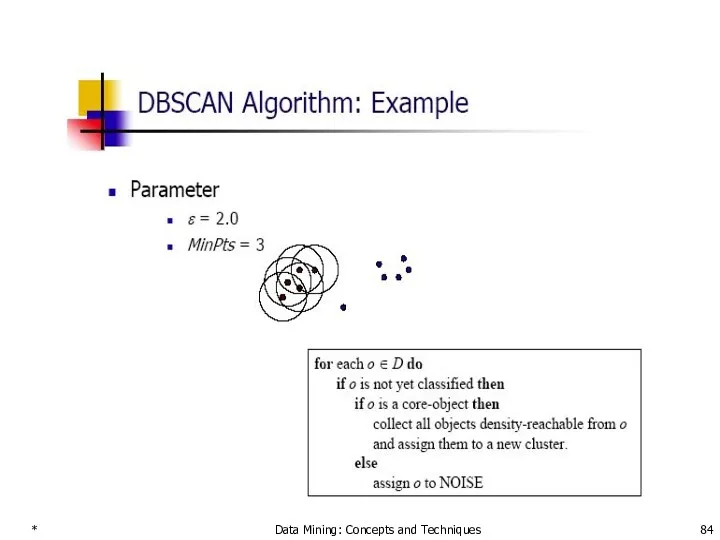
- 84. * Data Mining: Concepts and Techniques
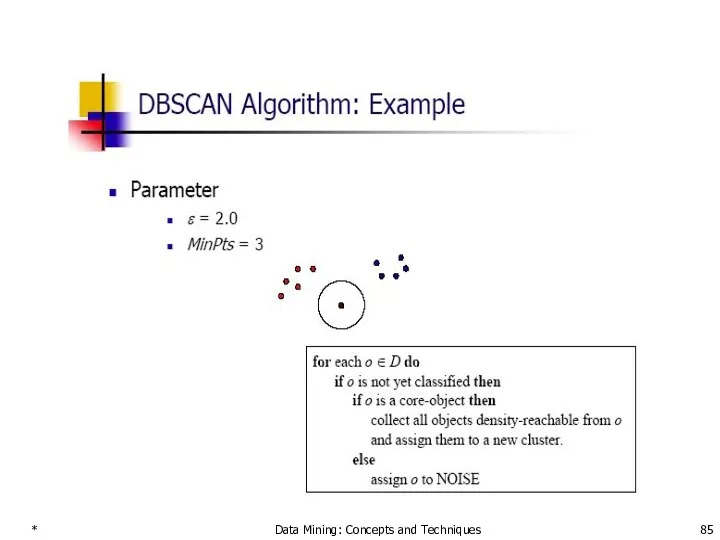
- 85. * Data Mining: Concepts and Techniques
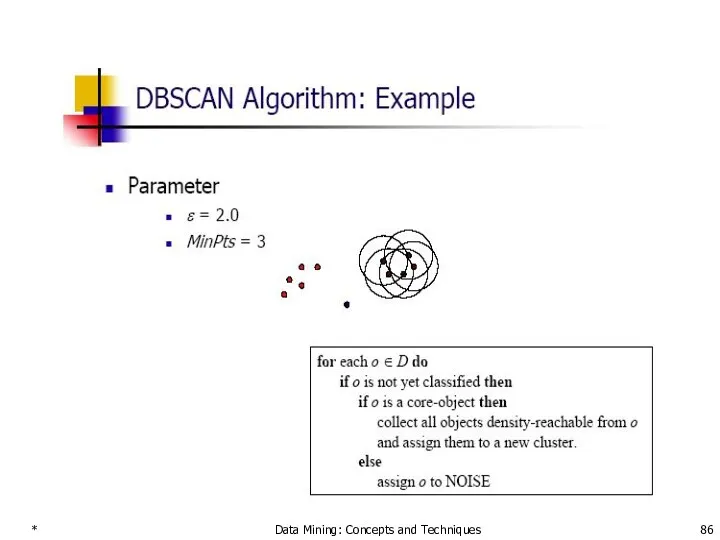
- 86. * Data Mining: Concepts and Techniques
- 87. * Data Mining: Concepts and Techniques
- 88. * Data Mining: Concepts and Techniques
- 89. * Data Mining: Concepts and Techniques Gradient: The steepness of a slope Example
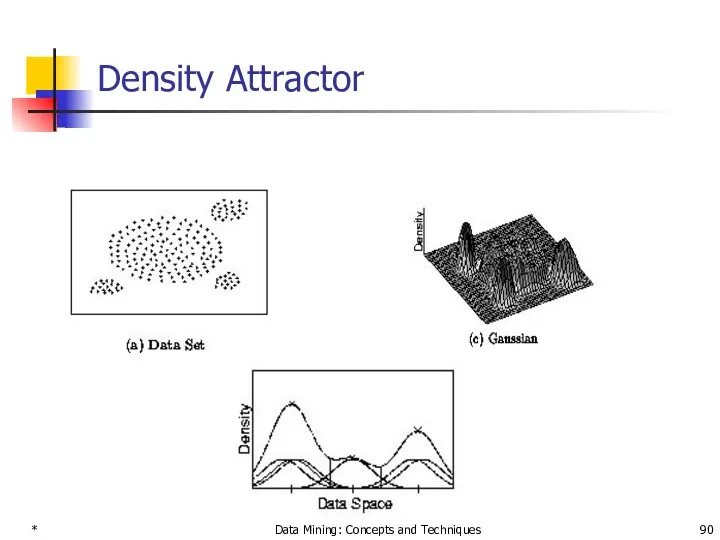
- 90. * Data Mining: Concepts and Techniques Density Attractor
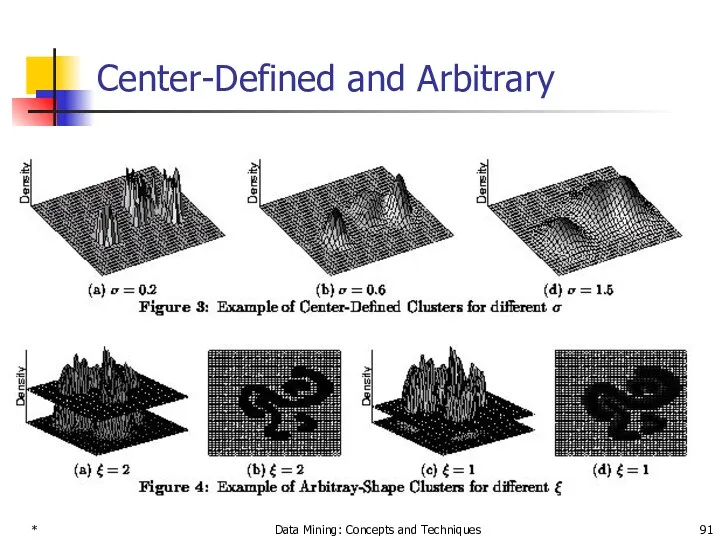
- 91. * Data Mining: Concepts and Techniques Center-Defined and Arbitrary
- 92. * Data Mining: Concepts and Techniques
- 93. * Data Mining: Concepts and Techniques
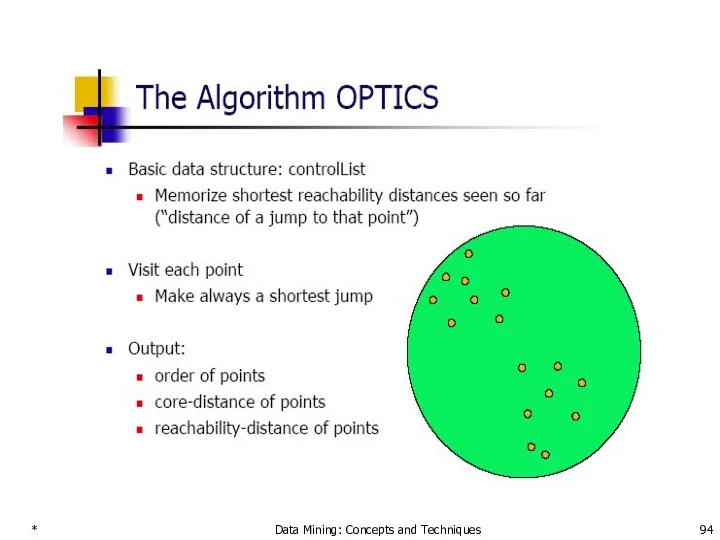
- 94. * Data Mining: Concepts and Techniques
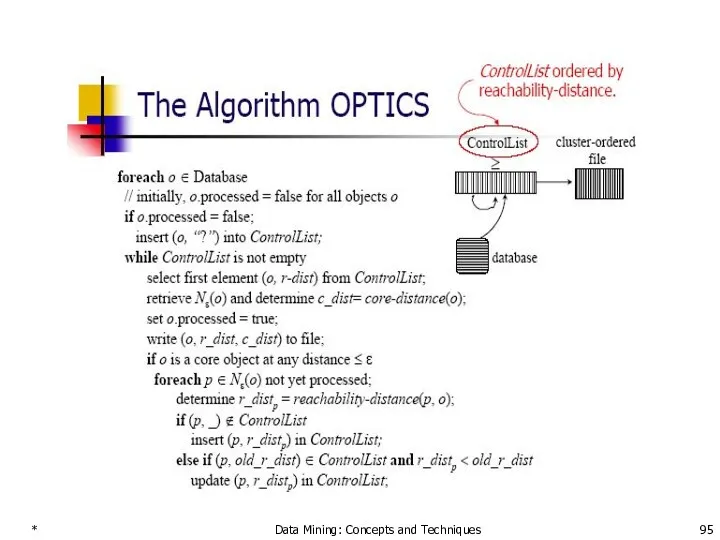
- 95. * Data Mining: Concepts and Techniques
- 96. * Data Mining: Concepts and Techniques
- 97. * Data Mining: Concepts and Techniques
- 98. * Data Mining: Concepts and Techniques Chapter 8. Cluster Analysis What is Cluster Analysis? Types of
- 99. * Data Mining: Concepts and Techniques Grid-Based Clustering Method Using multi-resolution grid data structure Several interesting
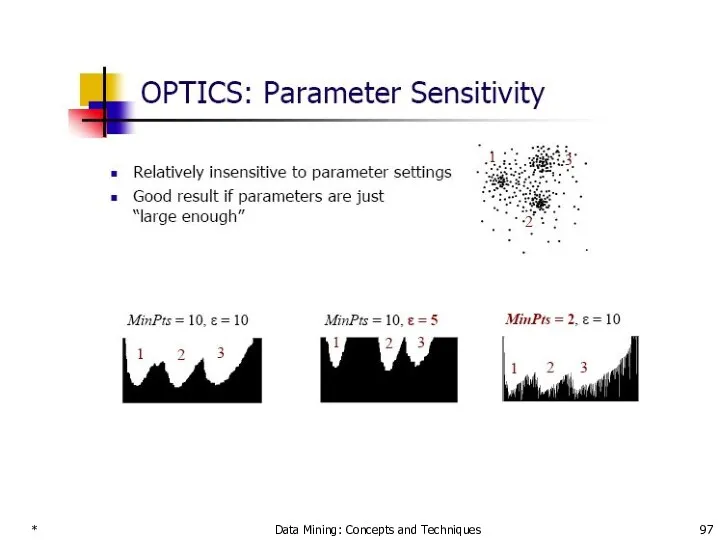
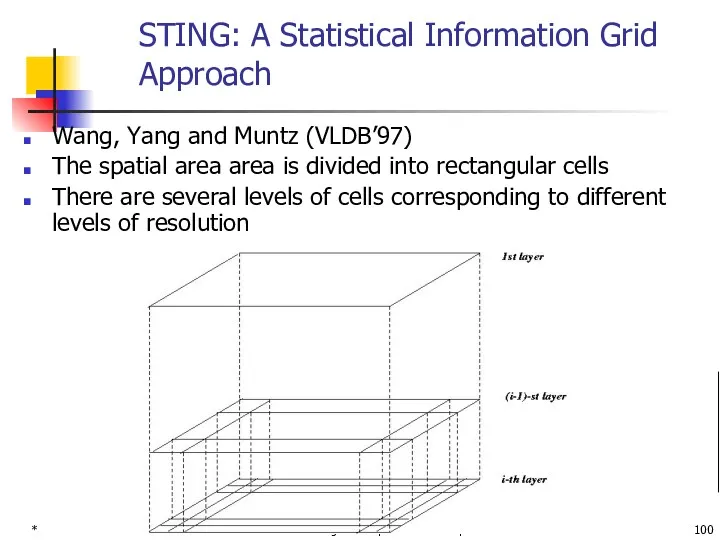
- 100. * Data Mining: Concepts and Techniques STING: A Statistical Information Grid Approach Wang, Yang and Muntz
- 101. STING: A Statistical Information Grid Approach (2) Each cell at a high level is partitioned into
- 102. STING: A Statistical Information Grid Approach (3) Remove the irrelevant cells from further consideration When finish
- 103. * Data Mining: Concepts and Techniques WaveCluster (1998) Sheikholeslami, Chatterjee, and Zhang (VLDB’98) A multi-resolution clustering
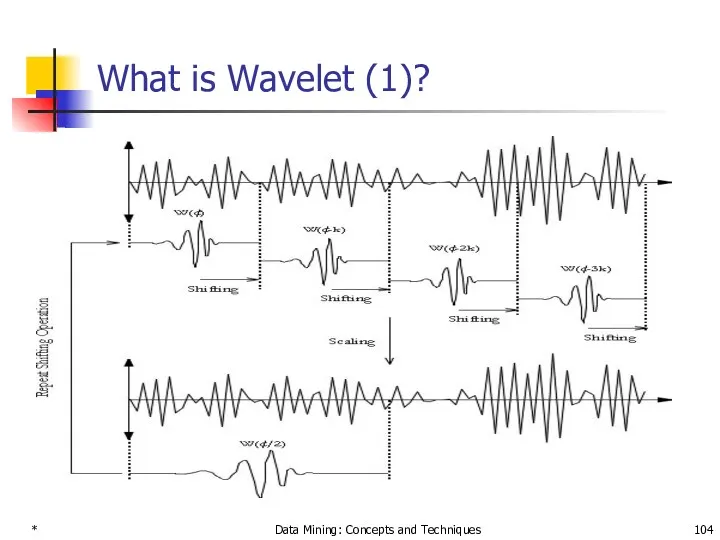
- 104. * Data Mining: Concepts and Techniques What is Wavelet (1)?
- 105. * Data Mining: Concepts and Techniques WaveCluster (1998) How to apply wavelet transform to find clusters
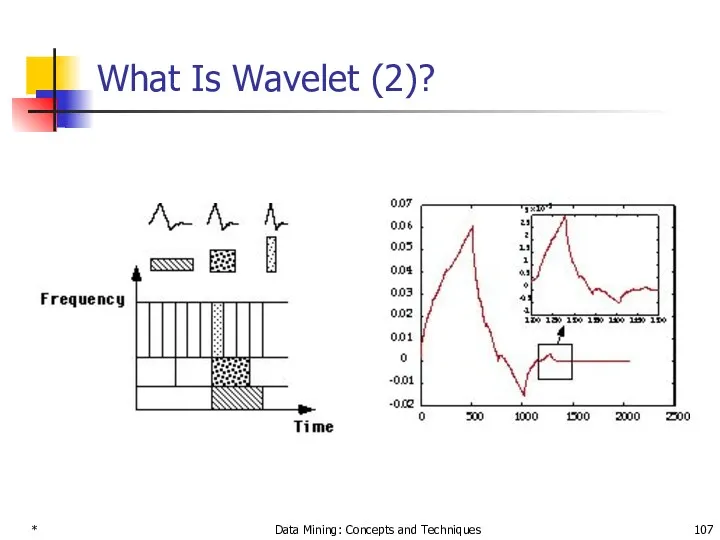
- 106. * Data Mining: Concepts and Techniques Wavelet Transform Decomposes a signal into different frequency subbands. (can
- 107. * Data Mining: Concepts and Techniques What Is Wavelet (2)?
- 108. * Data Mining: Concepts and Techniques Quantization
- 109. * Data Mining: Concepts and Techniques Transformation
- 110. * Data Mining: Concepts and Techniques WaveCluster (1998) Why is wavelet transformation useful for clustering Unsupervised
- 111. * Data Mining: Concepts and Techniques CLIQUE (Clustering In QUEst) Agrawal, Gehrke, Gunopulos, Raghavan (SIGMOD’98). Automatically
- 112. * Data Mining: Concepts and Techniques CLIQUE: The Major Steps Partition the data space and find
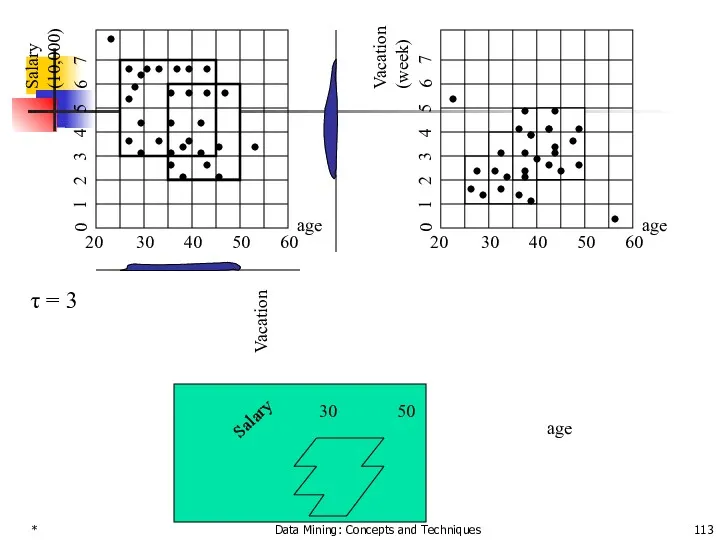
- 113. * Data Mining: Concepts and Techniques Salary (10,000) 20 30 40 50 60 age 5 4
- 114. * Data Mining: Concepts and Techniques Strength and Weakness of CLIQUE Strength It automatically finds subspaces
- 115. * Data Mining: Concepts and Techniques Chapter 8. Cluster Analysis What is Cluster Analysis? Types of
- 116. * Data Mining: Concepts and Techniques Model-Based Clustering Methods Attempt to optimize the fit between the
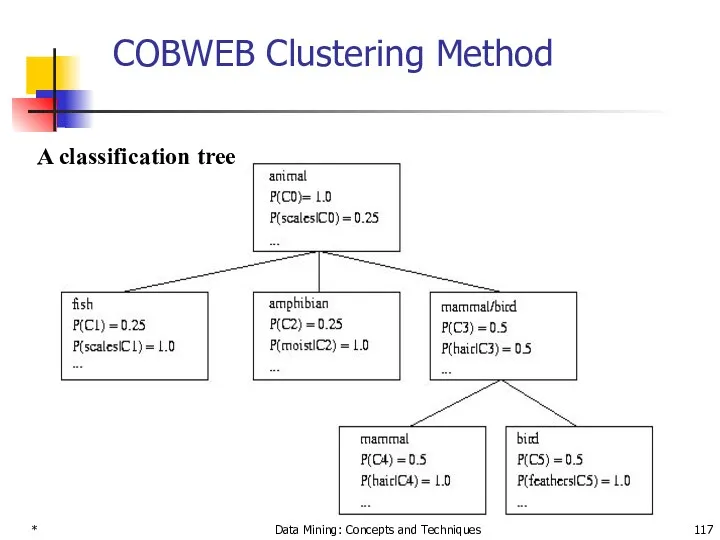
- 117. * Data Mining: Concepts and Techniques COBWEB Clustering Method A classification tree
- 118. * Data Mining: Concepts and Techniques More on Statistical-Based Clustering Limitations of COBWEB The assumption that
- 119. * Data Mining: Concepts and Techniques Other Model-Based Clustering Methods Neural network approaches Represent each cluster
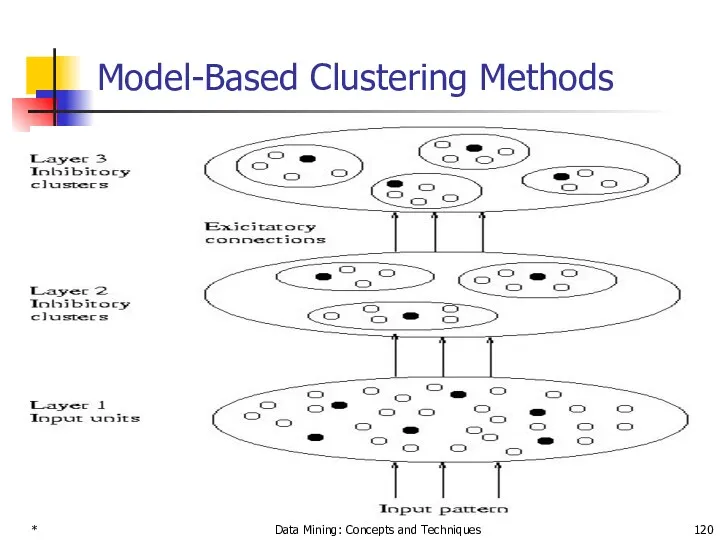
- 120. * Data Mining: Concepts and Techniques Model-Based Clustering Methods
- 121. * Data Mining: Concepts and Techniques Self-organizing feature maps (SOMs) Clustering is also performed by having
- 122. * Data Mining: Concepts and Techniques Chapter 8. Cluster Analysis What is Cluster Analysis? Types of
- 123. * Data Mining: Concepts and Techniques What Is Outlier Discovery? What are outliers? The set of
- 124. * Data Mining: Concepts and Techniques Outlier Discovery: Statistical Approaches Assume a model underlying distribution that
- 125. Outlier Discovery: Distance-Based Approach Introduced to counter the main limitations imposed by statistical methods We need
- 126. * Data Mining: Concepts and Techniques Outlier Discovery: Deviation-Based Approach Identifies outliers by examining the main
- 127. * Data Mining: Concepts and Techniques Chapter 8. Cluster Analysis What is Cluster Analysis? Types of
- 128. * Data Mining: Concepts and Techniques Problems and Challenges Considerable progress has been made in scalable
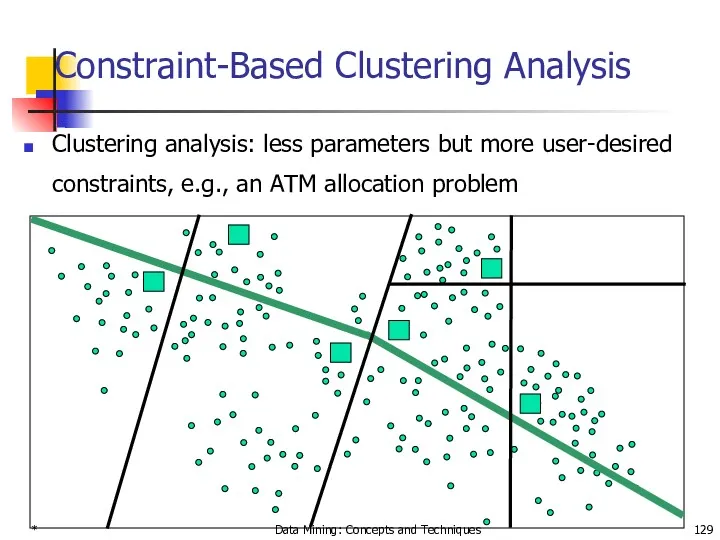
- 129. * Data Mining: Concepts and Techniques Constraint-Based Clustering Analysis Clustering analysis: less parameters but more user-desired
- 130. * Data Mining: Concepts and Techniques Clustering With Obstacle Objects Taking obstacles into account Not Taking
- 131. * Data Mining: Concepts and Techniques Summary Cluster analysis groups objects based on their similarity and
- 132. * Data Mining: Concepts and Techniques References (1) R. Agrawal, J. Gehrke, D. Gunopulos, and P.
- 134. Скачать презентацию



































































































 Характеристики відмінної вимоги. (Лекція 3.2)
Характеристики відмінної вимоги. (Лекція 3.2) Разработка урока обобщения и закрепления знаний, полученных при изучении курса Информатики в форме телевизионной игры Своя игра
Разработка урока обобщения и закрепления знаний, полученных при изучении курса Информатики в форме телевизионной игры Своя игра Графические возможности Matlab
Графические возможности Matlab Структурная методология
Структурная методология Специальные функции-члены класса. Лекция 11
Специальные функции-члены класса. Лекция 11 Телеканал ТВ Центр. Телевизионный сезон 2012-2013 гг
Телеканал ТВ Центр. Телевизионный сезон 2012-2013 гг Разработка ТЗ на новый SEO функционал на маркетплейсе
Разработка ТЗ на новый SEO функционал на маркетплейсе Общие сведения о языке программирования Паскаль. Начала программирования. Информатика. 8 класс
Общие сведения о языке программирования Паскаль. Начала программирования. Информатика. 8 класс Letters emails
Letters emails Облачные технологии
Облачные технологии Компьютерная сеть та модель – OSI
Компьютерная сеть та модель – OSI Структурированные кабельные системы
Структурированные кабельные системы Електронний щоденник засобами Delphi
Електронний щоденник засобами Delphi Коротка історія розвитку мов програмування
Коротка історія розвитку мов програмування Условный оператор if. Введение в программирование на языке Python
Условный оператор if. Введение в программирование на языке Python Информационные объекты различных видов
Информационные объекты различных видов Адресация компьютеров в сети
Адресация компьютеров в сети Changes in society by computing technology
Changes in society by computing technology Way the newspaper is made
Way the newspaper is made Архитектура СУБД Oracle. Основные понятия. (Лекция 2)
Архитектура СУБД Oracle. Основные понятия. (Лекция 2) Технология CSS
Технология CSS Презентация к Уроку Что такое алгоритм? Исполнители вокруг нас
Презентация к Уроку Что такое алгоритм? Исполнители вокруг нас Рекурсия. Описание подпрограмм
Рекурсия. Описание подпрограмм Турнир смекалистых
Турнир смекалистых Роботы будущего
Роботы будущего Использование функций в табличном процессоре MS EXCEL
Использование функций в табличном процессоре MS EXCEL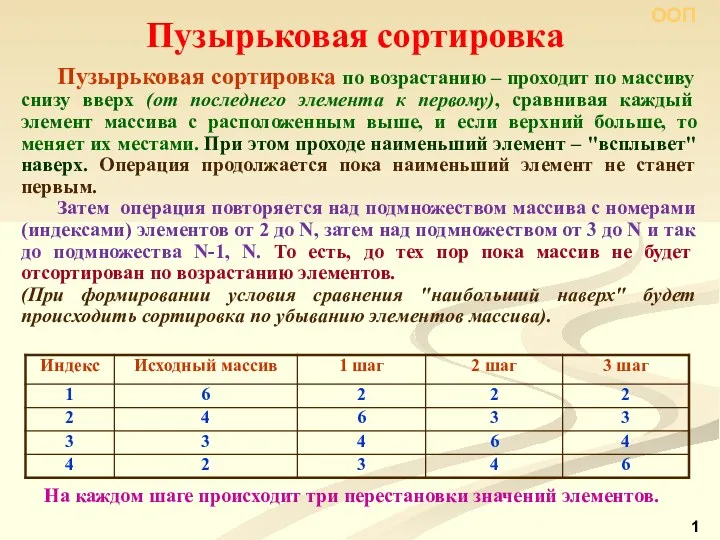 Пузырьковая сортировка
Пузырьковая сортировка Database systems
Database systems