Содержание
- 2. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ [ДП] — раздел математического программирования, совокупность приемов, позволяющих находить оптимальные решения, основанные на вычислении
- 3. задача оптимизации формулируется как конечный многошаговый процесс управления; целевая функция (выигрыш) является аддитивной и равна сумме
- 4. Принцип оптимальности лежит в основе метода ДП Впервые сформулированный в 1953 г. американским математиком Р.Э.Беллманом Формулировка
- 5. Ричард Эрнст Беллман Даты жизни: 26.08.1920-19.03.1984 Американский математик, один из ведущих специалистов в области математики и
- 6. При решении задачи на каждом шаге выбирается управление, которое должно привести к оптимальному выигрышу. Если считать
- 7. Общим для задач ДП является то, что переменные в модели рассматриваются не вместе, а последовательно, одна
- 8. Процесс решения при этом складывается из двух этапов. На первом он ведется “с конца”: для каждого
- 9. В задачах, решаемых методом динамического программирования, процесс управления разбивается на шаги (этапы). При распределении на несколько
- 10. Обозначим S0 – начальное состояние системы, Sn - конечное. В результате управления система последовательно переводится из
- 11. Схема решения задачи ДП … Sn
- 12. Владелец автомашины эксплуатирует ее в течение N лет. Известны затраты на содержание, ремонт и покупку нового
- 13. Шаговое управление - выбор одного из решений на год. Припишем первому решению численное значение 1, второму
- 14. задача о выборе траектории, задача последовательного принятия решения, задача об использовании рабочей силы, задача управления запасами.
- 15. Одной из важных экономических проблем является определение оптимальной стратегии в замене старых станков, агрегатов, машин на
- 16. Введем обозначения: r(t) — стоимость продукции, производимой за один год на единице оборудования возраста t лет;
- 17. Возраст оборудования отсчитывается в направлении течения процесса. Так, t = 0 соответствует случаю использования нового оборудования.
- 18. Функциональные уравнения, основанные на принципе оптимальности, имеют вид Уравнение (1) описывает N-стадийный процесс, а (2) —
- 19. Определить оптимальный цикл замены оборудования при следующих исходных данных: Р = 10, S(t) = 0, f(t)
- 20. Пример Для N = 1
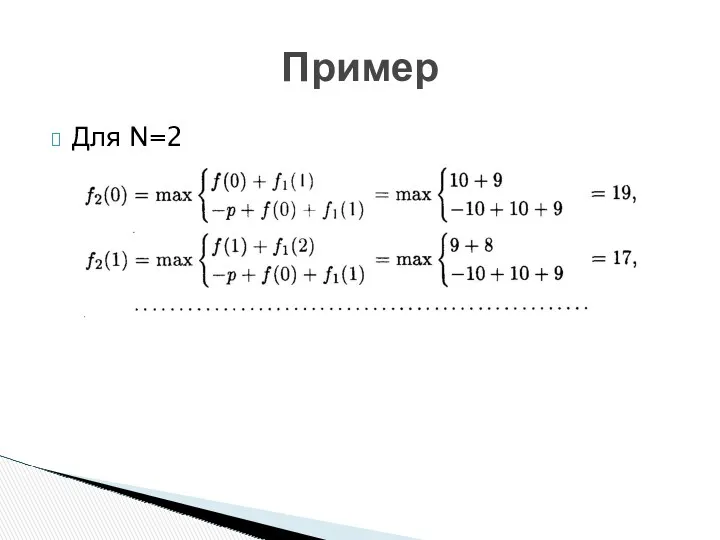
- 21. Для N=2 Пример
- 22. Пример
- 23. Пусть имеется некоторое количество ресурсов х, которое необходимо распределить между п различными предприятиями, объектами, работами и
- 24. Сформулированную задачу можно записать в математической форме: при ограничениях: Для решения задачи необходимо получить рекуррентное соотношение,
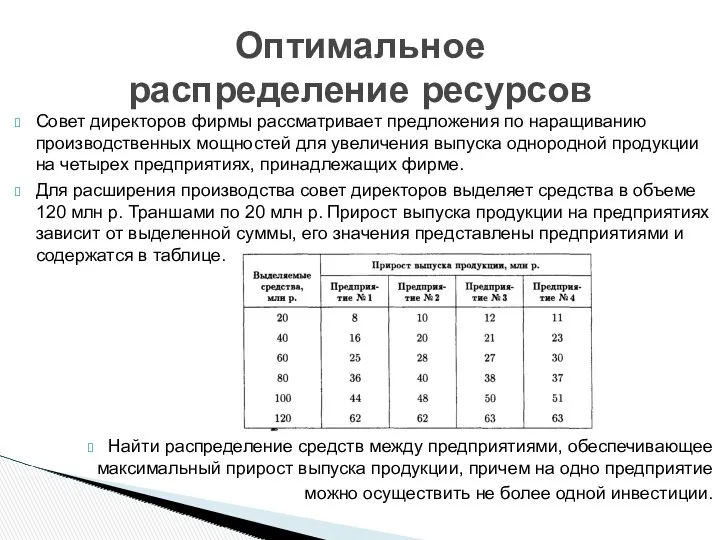
- 25. Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех
- 26. Рекуррентные соотношения будут иметь вид: для предприятия № 1 для всех остальных предприятий Решение будем проводить
- 27. 2-й этап. Инвестиции выделяем первому и второму предприятиям. Рекуррентное соотношение для 2-го этапа имеет вид Тогда
- 28. 3-й этап. Финансируем 2-й этап и третье предприятие. Расчеты проводим по формуле Тогда при х =
- 29. 4-й этап. Инвестиции в объеме 120 млн р. распределяем между 3-м этапом и четвертым предприятием. При
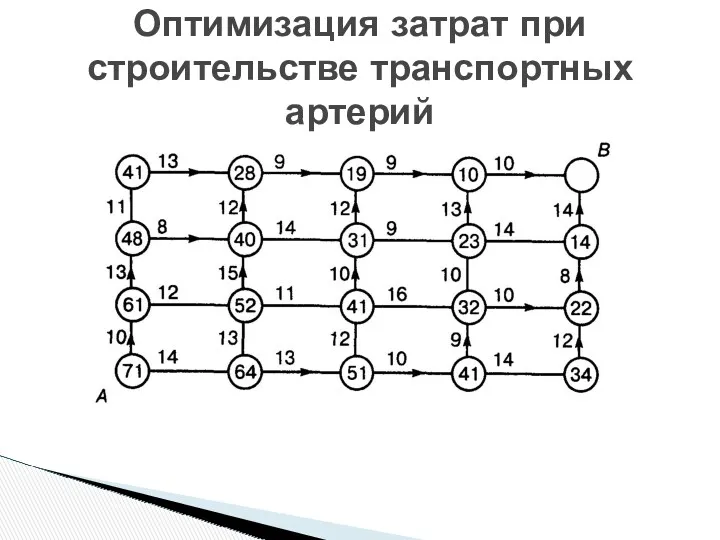
- 30. Требуется проложить путь (трубопровод, шоссе) между двумя пунктами А и В таким образом, чтобы суммарные затраты
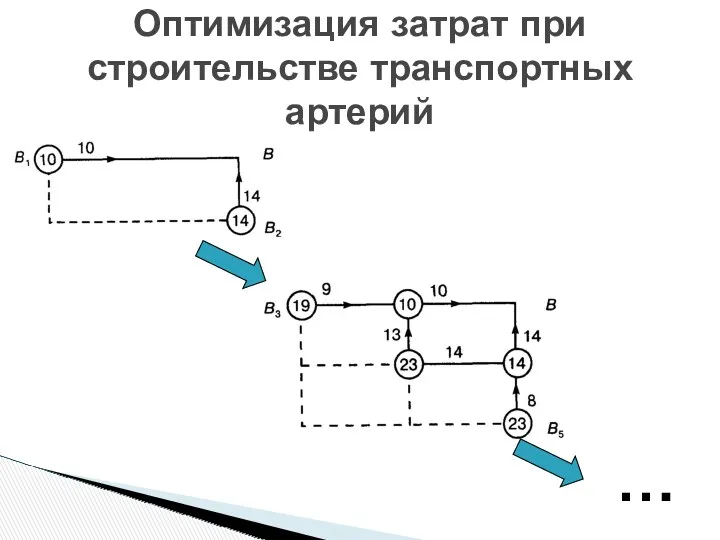
- 31. Оптимизация затрат при строительстве транспортных артерий …
- 32. Оптимизация затрат при строительстве транспортных артерий
- 34. Скачать презентацию
![ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ [ДП] — раздел математического программирования, совокупность приемов, позволяющих](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/393924/slide-1.jpg)


























 Система автоматизированного проектирования (САПР) AutoCAD
Система автоматизированного проектирования (САПР) AutoCAD Электронный бизнес
Электронный бизнес Презентация к уроку информатики Объекты Базы Данных. Запросы
Презентация к уроку информатики Объекты Базы Данных. Запросы Информация. Свойства информации. Представление информации в ЭВМ. Единицы измерения информации. (Лекция 3)
Информация. Свойства информации. Представление информации в ЭВМ. Единицы измерения информации. (Лекция 3) Различные подходы к измерению количества информации
Различные подходы к измерению количества информации Структура вычислительной системы и место курса в общем цикле курсов по информатике
Структура вычислительной системы и место курса в общем цикле курсов по информатике Восьмеричная система счисления
Восьмеричная система счисления Автоматизація контролю працездатності серверів на базі Arduino
Автоматизація контролю працездатності серверів на базі Arduino Глубокий массафол и другие методы продвижения аккаунтов инстаграм
Глубокий массафол и другие методы продвижения аккаунтов инстаграм Facebook - социальная сеть
Facebook - социальная сеть Diffie-Hellman Key Agreement Method
Diffie-Hellman Key Agreement Method Средства защиты информации в ОС Windows и Unix. (Лекция 10)
Средства защиты информации в ОС Windows и Unix. (Лекция 10) Разработка презентационных материалов предприятия, организации. Заготовки публикаций в Publisher
Разработка презентационных материалов предприятия, организации. Заготовки публикаций в Publisher Отображение XML в браузере. (Лекция 2)
Отображение XML в браузере. (Лекция 2) Алфавитный подход к измерению информации
Алфавитный подход к измерению информации Презентация по теме Общение в Интернете
Презентация по теме Общение в Интернете Модульное программирование
Модульное программирование Компьютерная локальная сеть в ЗАГСе
Компьютерная локальная сеть в ЗАГСе Двоичные вычитатели
Двоичные вычитатели Цифровое портфолио
Цифровое портфолио Файловая система ОС Windows
Файловая система ОС Windows Цифровой звук (8 класс)
Цифровой звук (8 класс) Дискретизация. Виды информации
Дискретизация. Виды информации Методика разработки, ориентированная на повышение параллельности
Методика разработки, ориентированная на повышение параллельности Основные понятия и принципы работы системы AutoCAD
Основные понятия и принципы работы системы AutoCAD Программируем в Windows Forms
Программируем в Windows Forms CD-диск
CD-диск Программирование на Python. Урок 11. Взаимодействие объектов
Программирование на Python. Урок 11. Взаимодействие объектов