Содержание
- 2. Автоморфизмы графа. Пример. α0 =(a)(b)(c)(d); α1=(a c)(b)(d); α2=(b d) (a) (c); α3=(a c) (b d);
- 3. Подгруппа группы А – группа . Подгруппа группы А - группа , где M1 замкнуто относительно
- 4. Стабилизаторы А – группа подстановок на множестве Х. Стабилизатор А(х) элемента х – подгруппа группы А,
- 5. Орбиты А – группа подстановок на множестве Х. Орбита θ(х) элемента х – подмножество множества Х,
- 6. Изоморфизм Вершинная группа Г(G) индуцирует рёберную Г1(G). Для связных p,q графов с p≥3группы Г(G) и Г1(G)
- 7. Изоморфизм α0 =(a)(b)(c)(d); α1=(a c)(b)(d); α2=(b d) (a) (c); α3=(a c) (b d). β0 =(x)(y)(z)(u)(w); β1
- 8. Изоморфизм Рёберная и вершинная группы графа G изоморфны ⇔ G имеет не более одной изолированной вершины,
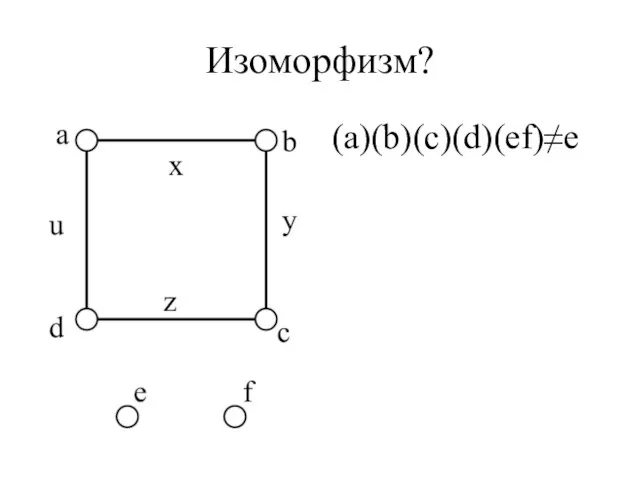
- 9. Изоморфизм? (a)(b)(c)(d)(ef)≠e
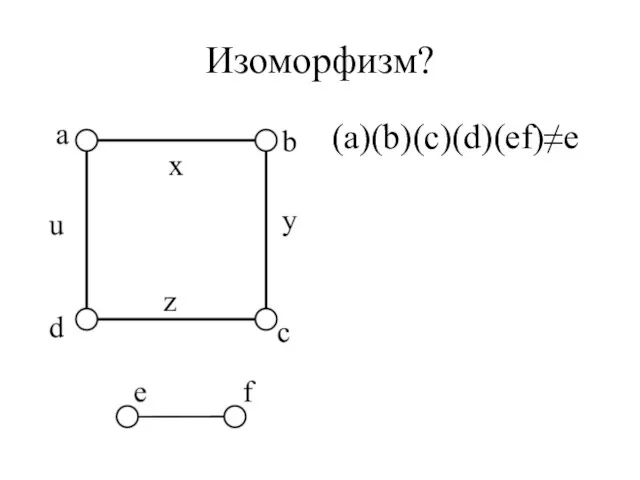
- 10. Изоморфизм? (a)(b)(c)(d)(ef)≠e
- 11. Операции над группами Пусть даны группы автоморфизмов Г(Ga)= 〈A,°〉 и Г(Gb)= 〈B,°〉 . ⏐A⏐ - порядок
- 12. Сложение групп Г= Г(Ga)+Г(Gb) Группа Г действует на множестве Va∪Vb. Степень группы Г равна ⏐Va⏐+⏐Vb⏐. Порядок
- 13. Пример. Сложение групп Дано: ©П.Порешин
- 14. Перечисление графов Умножение групп Г= Г(Ga) × Г(Gb) Группа Г действует на Va × Vb={(x,y)⏐x∈Va, y∈Vb}
- 15. Произведение групп Дано: ©П.Порешин
- 16. Перечисление графов Композиция групп Действует на Va × Vb={(x,y)⏐x∈Va, y∈Vb} Степень группы Г равна d*e Порядок
- 17. Операции на группах подстановок
- 18. Классификация групп подстановок степени p
- 19. Теоремы Группа Г(G) - Sn⇔ G=Kn или G = Если G - простой цикл длины n,
- 20. Теоремы Граф и его дополнение имеют одну и ту же группу: Г(G) =Г Если G1 и
- 21. Простой граф Не тривиальный граф G называется простым, если разложение G=G1×G2 возможно тогда, когда или G1
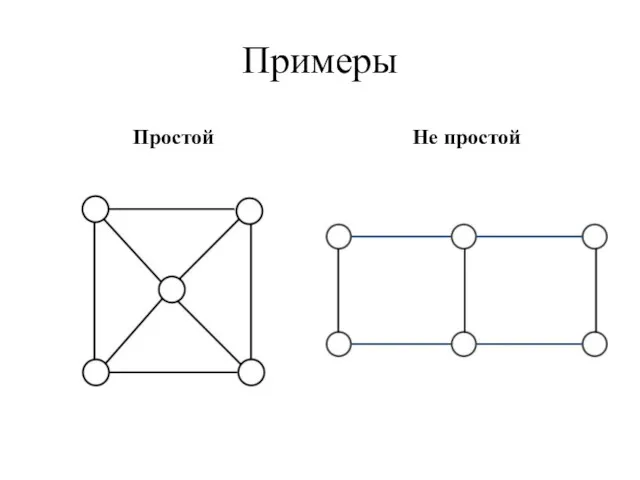
- 22. Примеры Простой Не простой
- 23. Группа произведения Группа произведения идентична произведению их групп, т.е. Г(G1×G2)= Г(G1)×Г(G2) ⇔ G1 и G2 –
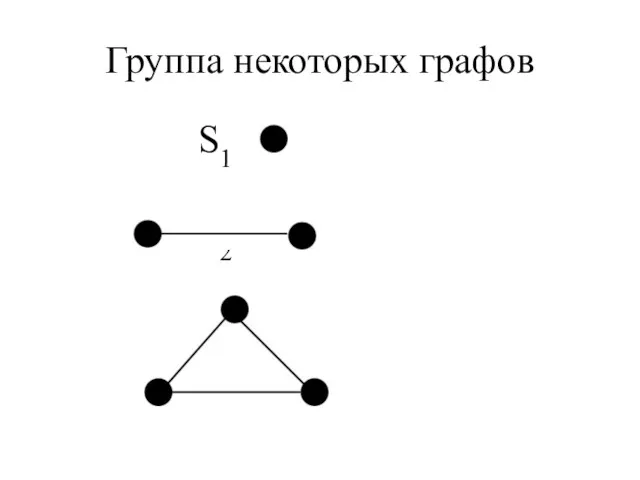
- 24. Группа некоторых графов S1 S2 S3
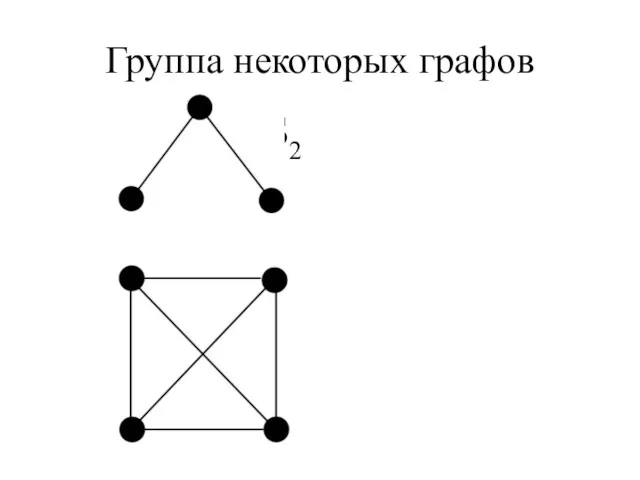
- 25. Группа некоторых графов E1 +S2 S4
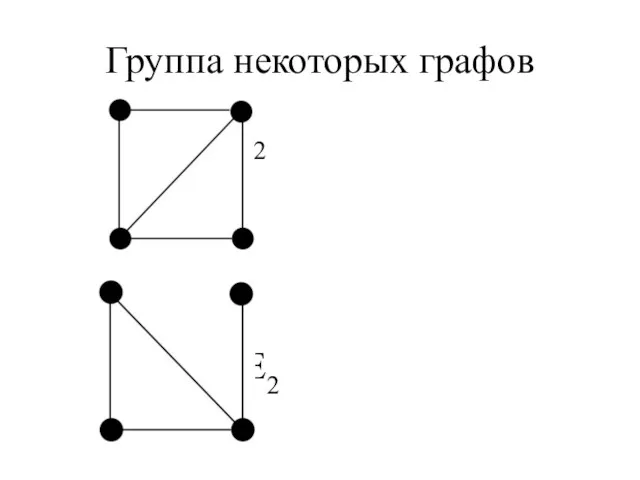
- 26. Группа некоторых графов S2+S2 S2+E2
- 27. Число способов пометить граф Помечаются вершины p,q графа числами от 1 до p. Теорема: Данный граф
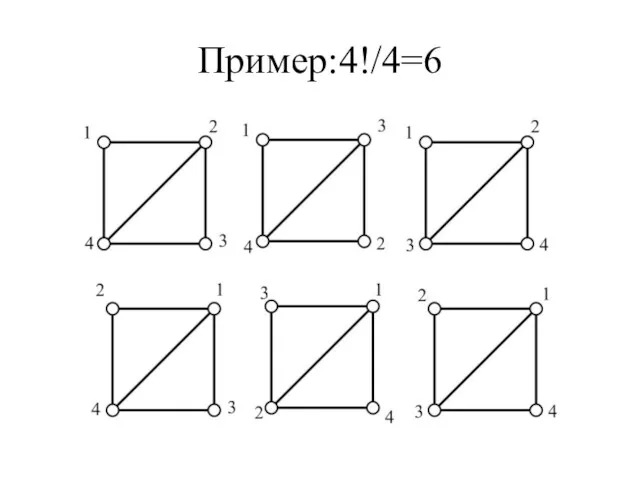
- 28. Пример:4!/4=6
- 29. Цикловой индекс группы А – группа порядка m и степени d (1j1+2j2+...djd= d для любой α∈A)
- 30. Цикловой индекс группы. Пример α0 =(a)(b)(c)(d); α1=(a c)(b)(d); α2=(b d) (a) (c); α3=(a c) (b d);
- 31. Цикловой индекс группы. Пример β0 =(x)(y)(z)(u)(w); β1 =(ux)(yz)(w); β2 =(xy)(uz)(w); β3 =(xz)(uy)(w); s15 s22s11 s22s11 s22s11
- 32. К теореме Пойа D -область определения, R - множество значений, - весовая функция, приписывающая каждому r∈R
- 33. К теореме Пойа Объекты, подлежащие счёту – функции из D в R. Элементы области определения –
- 34. К теореме Пойа Пусть имеется cmn фигур с весом (m,n) и Сmn конфигураций с весом xmyn.
- 35. Теорема Пойа Если записать Z(A)=Z(A;a1, a1,… ad), то для любой функции h(x,y) Z(А,h(x,y))=Z(A; h(x,y), h(x2,y2),… h(xd,yd))
- 36. Теорема Пойа. Пример. Z(А,h(x,y))=Z(A; h(x,y), h(x2,y2),… h(xd,yd)) h(x,y)=x+y, h(x2,y2)=x2+y2
- 37. Теорема Пойа. Пример.
- 38. Теорема Пойа. Пример. Z(A)=1/4(x4+4x3y+6 x2y2+4xy3 +y4 +2(x2+y2 ) (x2+2xy+y2 ) + x4+ 2x2y2 +y4) = 1/4(2x4+4x3y+8x2y2+4xy3
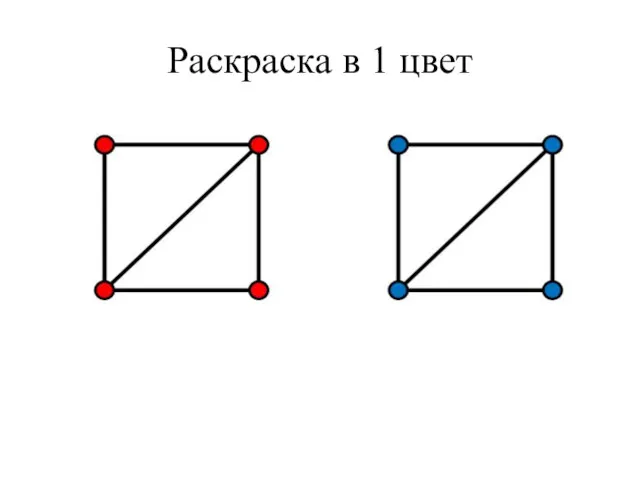
- 39. Раскраска в 1 цвет
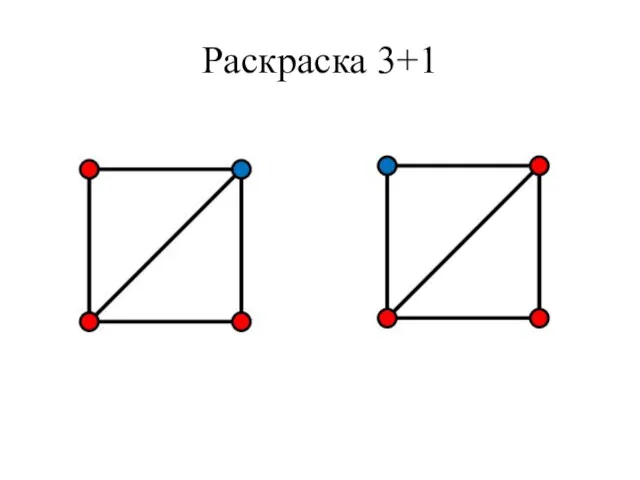
- 40. Раскраска 3+1
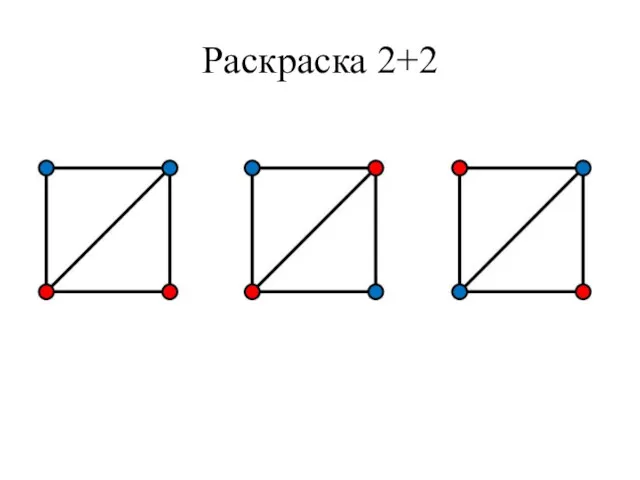
- 41. Раскраска 2+2
- 42. Оптимизационные алгоритмы Нахождение оптимальных решений для взвешенных графов
- 43. Минимальное стягивающее дерево для ориентированного графа v0- корень, каждая вершина достижима из v0. Стягивающее дерево –
- 44. Минимальное стягивающее дерево для взвешенного ориентированного графа Алгоритм Строим произвольное стягивающее дерево. Идём по дереву от
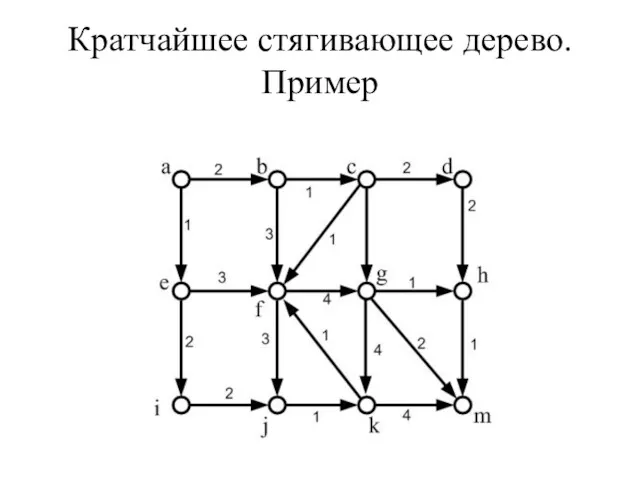
- 45. Кратчайшее стягивающее дерево. Пример
- 46. Критический (самый длинный) путь (Задача сетевого планирования). Нумеруем вершины (если есть дуга (xi,xj), то i L(xi)
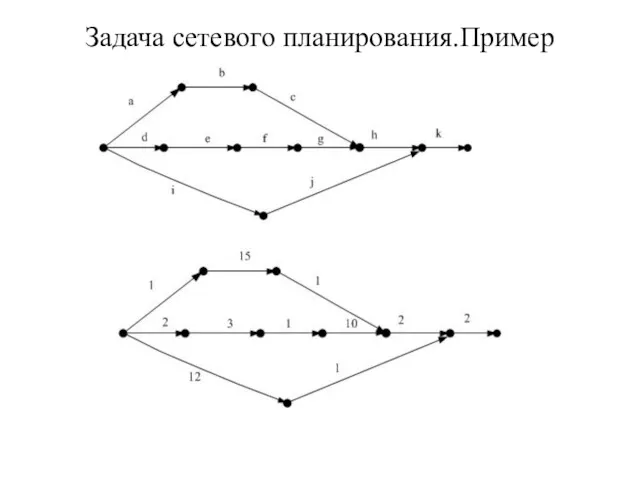
- 47. Задача сетевого планирования. Пример. Требуется установить электродвигатель на фундаментной плите. В операцию входят следующие работы: оформление
- 48. Задача сетевого планирования.Пример
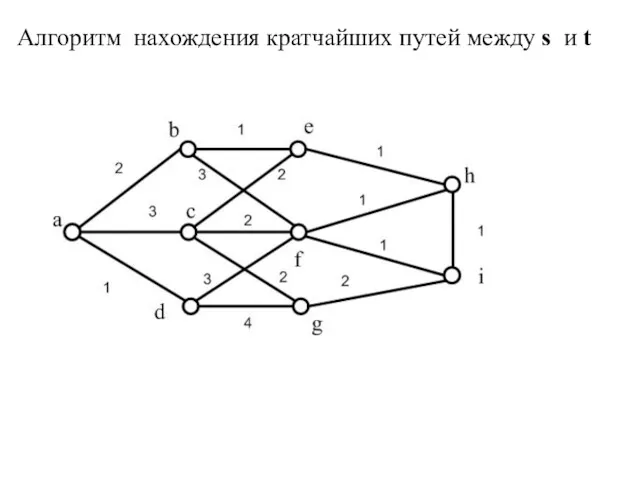
- 49. Алгоритм нахождения кратчайших путей между s и t Взвешенный неориентированный граф Dist(s)=0 , считаем пометку постоянной.
- 50. Алгоритм нахождения кратчайших путей между s и t Среди всех вершин выбираем xi* такую, что Dist(xi*)=min{
- 51. Алгоритм нахождения кратчайших путей между s и t
- 53. Скачать презентацию





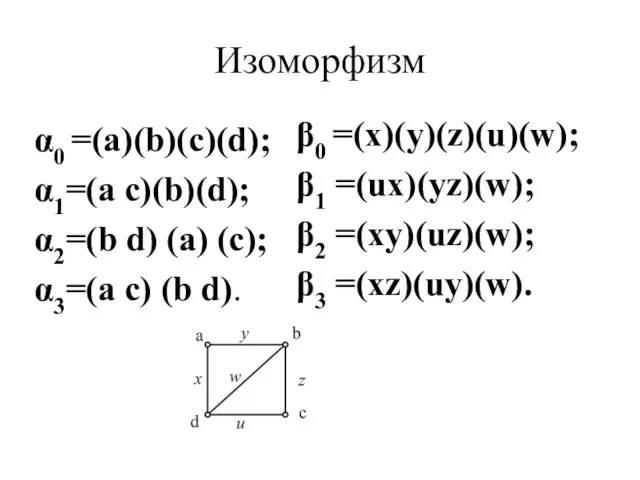































 Технологии программирования. Строки
Технологии программирования. Строки Разработка информационной системы инвентаризации компьютеров в сети для предприятия
Разработка информационной системы инвентаризации компьютеров в сети для предприятия Параметры страницы. Форматирование текста
Параметры страницы. Форматирование текста 3D печать. Будущее и перспективы. (Часть 1)
3D печать. Будущее и перспективы. (Часть 1) Вероятностный подход к определению количества информации.
Вероятностный подход к определению количества информации. Пример кейса-референса
Пример кейса-референса Проектирование баз данных
Проектирование баз данных Память и виды памяти
Память и виды памяти Практическая работа Устройства компьютера. Адрес клетки
Практическая работа Устройства компьютера. Адрес клетки Powerpoint бағдарламасымен жұмыс жасау
Powerpoint бағдарламасымен жұмыс жасау Безопасность в сети Интернет
Безопасность в сети Интернет Локальные сети. Параметры сетей и их стандарты
Локальные сети. Параметры сетей и их стандарты Нестандартные периферийные устройства ПК
Нестандартные периферийные устройства ПК Информационная безопасность
Информационная безопасность fbea8-fe014e85
fbea8-fe014e85 Электронные российские учебники
Электронные российские учебники Таблицы в MsWord
Таблицы в MsWord Creating Functions and Debugging Subprograms
Creating Functions and Debugging Subprograms Моделирование. Модели и моделирование
Моделирование. Модели и моделирование Что такое CSS
Что такое CSS Сведения о программе 1С: Предприятие
Сведения о программе 1С: Предприятие Программирование на Python. Урок 11. Взаимодействие объектов
Программирование на Python. Урок 11. Взаимодействие объектов Информатика 10-11 класс тема Логика
Информатика 10-11 класс тема Логика Массивы
Массивы Язык С++. Введение в С++
Язык С++. Введение в С++ Как составить техническое задание?
Как составить техническое задание? Дополнительная литература для лекций курса - Основы тестирования ПО
Дополнительная литература для лекций курса - Основы тестирования ПО Открытый урок
Открытый урок