Содержание
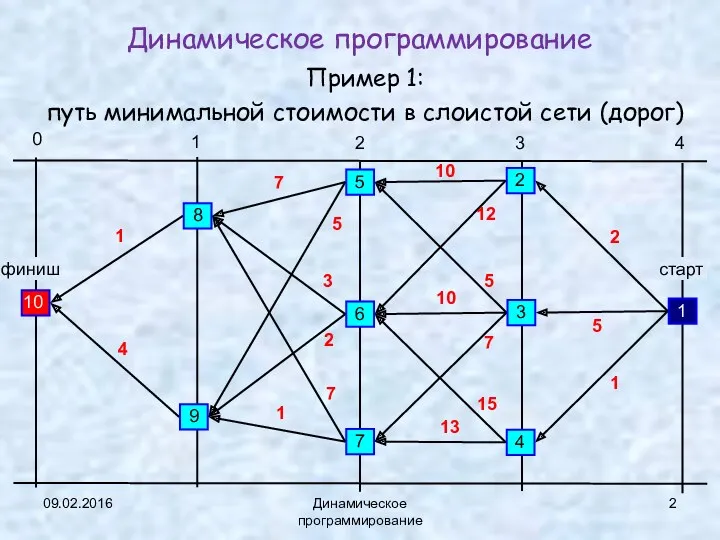
- 2. 09.02.2016 Динамическое программирование Динамическое программирование Пример 1: путь минимальной стоимости в слоистой сети (дорог)
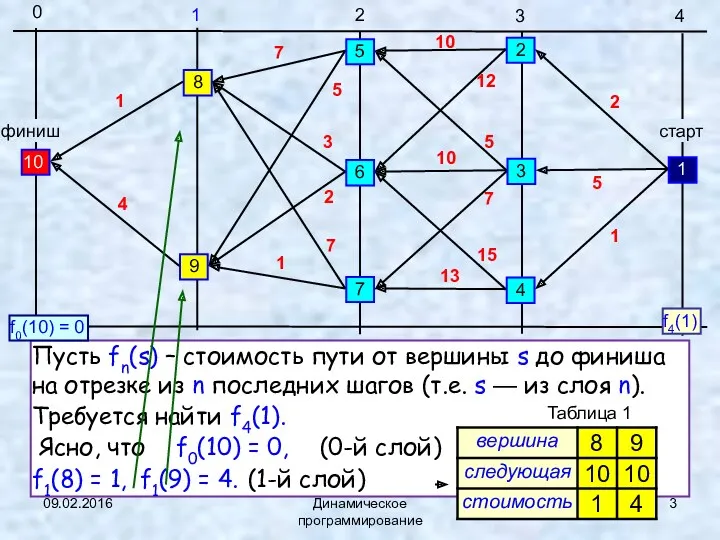
- 3. 09.02.2016 Динамическое программирование Пусть fn(s) – стоимость пути от вершины s до финиша на отрезке из
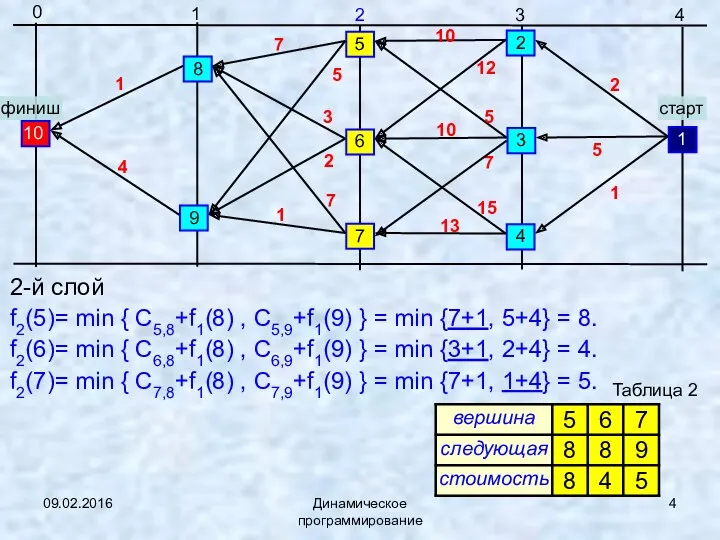
- 4. 09.02.2016 Динамическое программирование 2-й слой f2(5)= min { C5,8+f1(8) , C5,9+f1(9) } = min {7+1, 5+4}
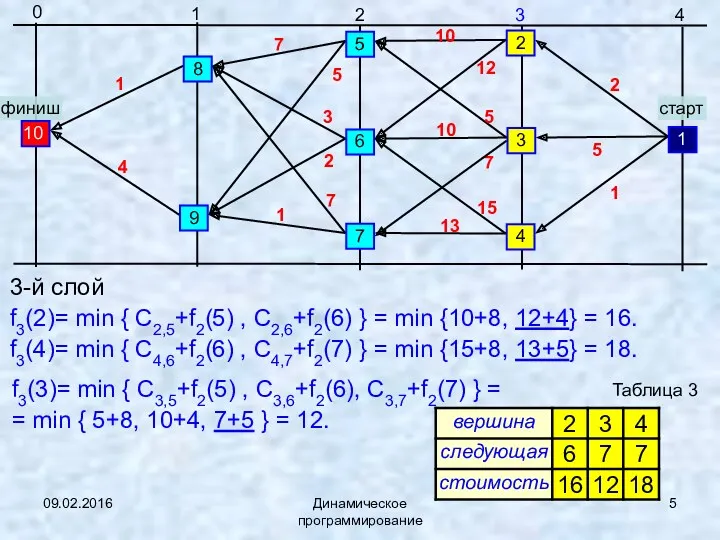
- 5. 09.02.2016 Динамическое программирование 3-й слой f3(2)= min { C2,5+f2(5) , C2,6+f2(6) } = min {10+8, 12+4}
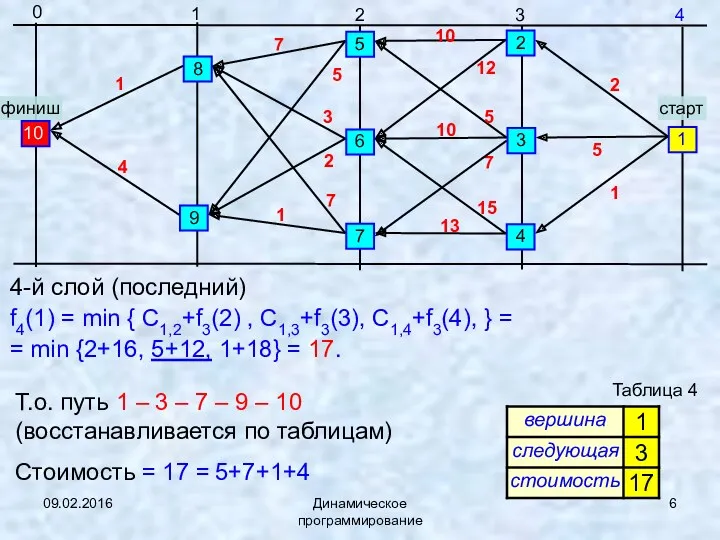
- 6. 09.02.2016 Динамическое программирование 4-й слой (последний) f4(1) = min { C1,2+f3(2) , C1,3+f3(3), C1,4+f3(4), } =
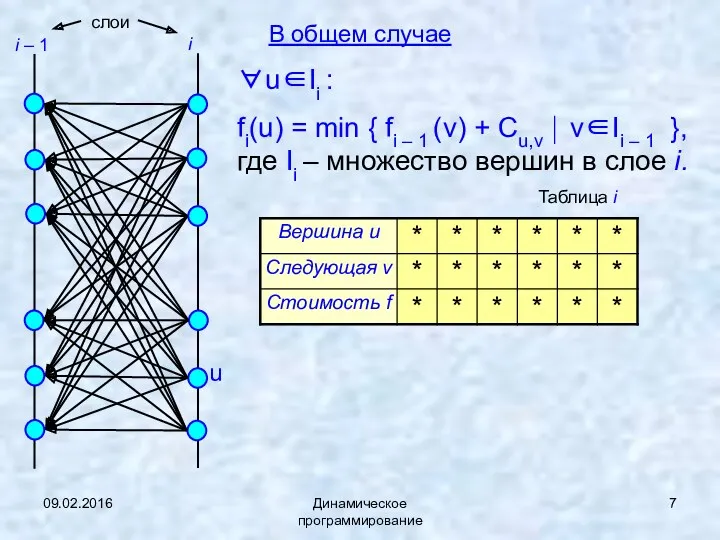
- 7. 09.02.2016 Динамическое программирование В общем случае i – 1 i слои ∀u∈Ii : fi(u) = min
- 8. 09.02.2016 Динамическое программирование Основные особенности метода ДП Рекуррентное соотношение Большая задача решается на основе решений меньших
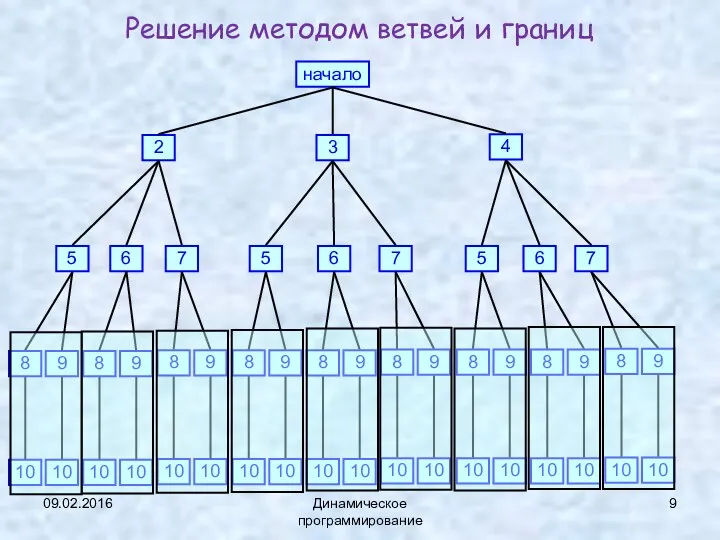
- 9. 09.02.2016 Динамическое программирование Решение методом ветвей и границ начало 3 2 4 5 6 7 5
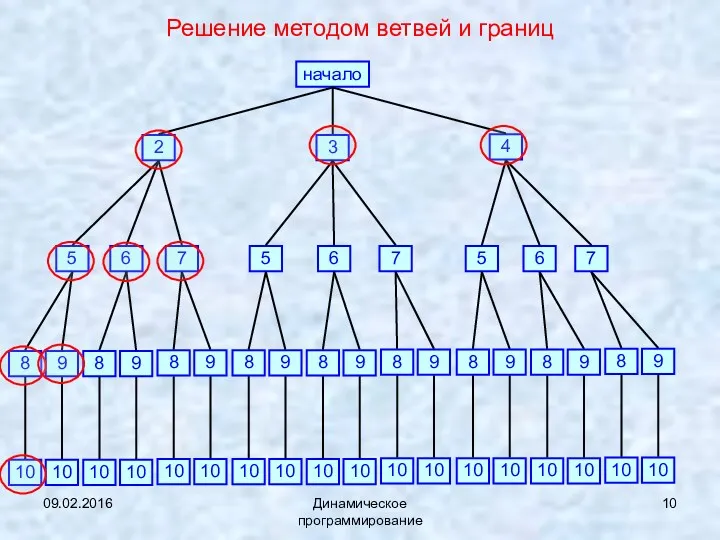
- 10. 09.02.2016 Динамическое программирование Решение методом ветвей и границ начало 3 2 4 5 6 7 5
- 11. 09.02.2016 Динамическое программирование Динамическое программирование. Пример 2: Задача о порядке перемножения матриц Рассмотрим произведение матриц M1
- 12. 09.02.2016 Динамическое программирование Задача о порядке перемножения матриц Общее количество элементарных операций умножения, требуемое при вычислении
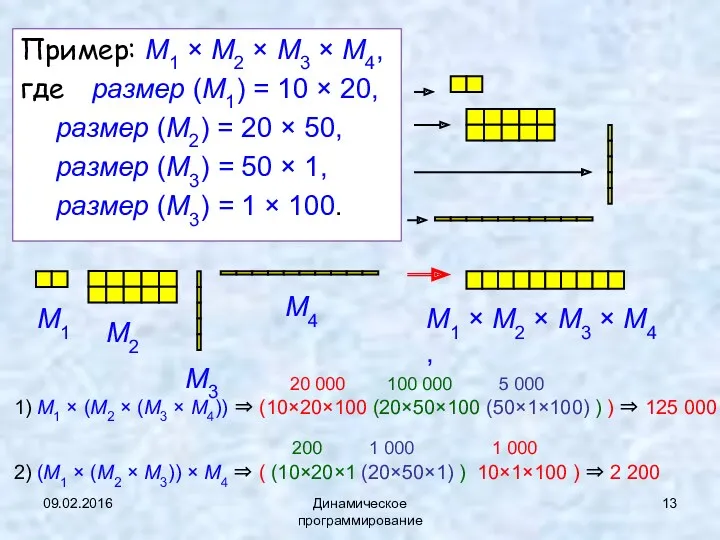
- 13. 09.02.2016 Динамическое программирование Пример: M1 × M2 × M3 × M4, где размер (M1) = 10
- 14. 09.02.2016 Динамическое программирование Рекуррентное соотношение Пусть mij – оптимальное количество умножений, требуемое для вычисления произведения цепочки
- 15. 09.02.2016 Динамическое программирование 1) Заметим, что в правой части равенства разности индексов k – i и
- 16. 09.02.2016 Динамическое программирование В ячейках таблицы T(i, j) хранятся вычисленные значения mij и те значениея qij
- 17. 09.02.2016 Динамическое программирование Алгоритм вычисляет оптимальное значение m1n и заполняет таблицу T по строкам сверху вниз:
- 18. for (i = 1; i for (L = 1; L for (i = 1; i j
- 19. 09.02.2016 Динамическое программирование Характеристики алгоритма Алгоритм требует: порядка n 2/2 элементов памяти для хранения таблицы около
- 20. 09.02.2016 Динамическое программирование Пример вычисления M1 × M2 × M3 × M4 (см. слайд 13) Для
- 21. 09.02.2016 Динамическое программирование Строка таблицы при L= 2 m1,3 = Min {m1k + mk +1,3 +
- 22. 09.02.2016 Динамическое программирование Последняя строка таблицы (из одной ячейки) Т (1, 4): m1,4 = Min {
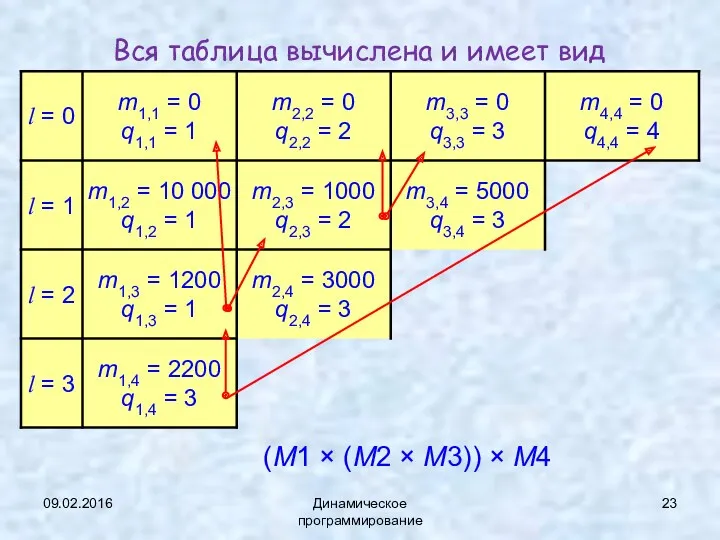
- 23. 09.02.2016 Динамическое программирование Вся таблица вычислена и имеет вид (M1 × (M2 × M3)) × M4
- 24. 09.02.2016 Динамическое программирование В общем случае порядок перемножения матриц легко определить рекурсивно. Пусть имеется функция перемножения
- 25. «Набросок» функции перемножения цепочки матриц: // Псевдокод Matrix MatrixSeqMult ( int i, int j) // i
- 26. 09.02.2016 Динамическое программирование Полезно сравнить решение, полученное методом динамического программирования, с решением методом ветвей и границ.
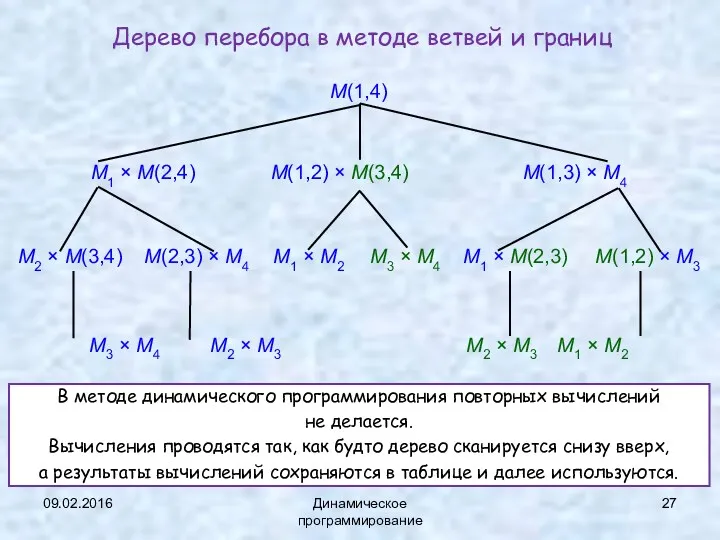
- 27. 09.02.2016 Динамическое программирование Дерево перебора в методе ветвей и границ M(1,4) M1 × M(2,4) M(1,2) ×
- 28. 09.02.2016 Динамическое программирование Оценка количества узлов дерева Оценить количество узлов дерева в общем случае можно подсчётом
- 29. 09.02.2016 Динамическое программирование Начальное условие p1 = 1. Далее p2 = p1 p1 = 1, p3
- 30. 09.02.2016 Динамическое программирование Тогда для чисел Каталана при больших значениях n справедливо т. е. число узлов
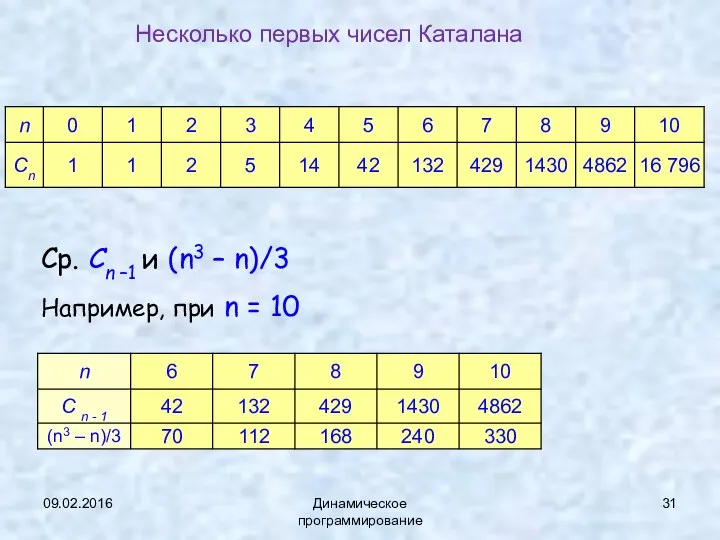
- 31. 09.02.2016 Динамическое программирование Несколько первых чисел Каталана Ср. Сn –1 и (n3 – n)/3 Например, при
- 32. Пример 3. Оптимальные деревья поиска Ранее при рассмотрении БДП, как правило, предполагалось, что для поиска различные
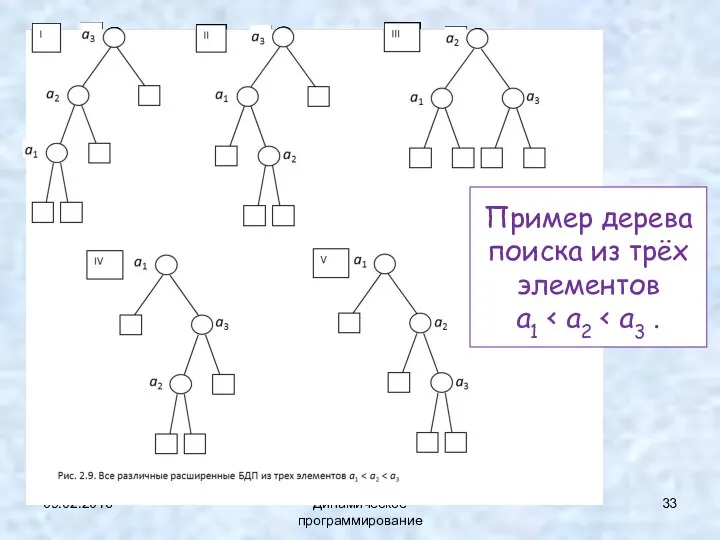
- 33. 09.02.2016 Динамическое программирование Пример дерева поиска из трёх элементов a1
- 34. Заданы вероятности предъявления элемента x для поиска: P (x = a1) = α; P (x =
- 35. Постановка задачи Поиск будет осуществляться среди набора данных a1, a2, …, an–1, an. Пусть последовательность упорядочена:
- 36. Все эти 2n + 1 событий (исходов поиска) могут быть упорядочены: B0 Заданы вероятности (или частоты)
- 37. Тогда среднее число (математическое ожидание) сравнений при поиске можно записать в виде где l (x) –
- 38. Такое дерево называют оптимальным БДП. Есть ли сходство этой задачи с задачей построения оптимального префиксного кода
- 39. Напоминание Задача построения оптимального префиксного кода есть задача минимизации функции L = Σi =1..n wi li
- 40. 09.02.2016 Динамическое программирование Итак, … Есть ли сходство этой задачи с задачей построения оптимального префиксного кода
- 41. Очевидное решение поставленной задачи состоит в переборе всех структурно различных бинарных деревьев с n узлами и
- 42. Решение поставленной задачи методом динамического программирования на следующей лекции. 09.02.2016 Динамическое программирование
- 44. Скачать презентацию




























 Стенд intel Isef. Как правильно сделать постер
Стенд intel Isef. Как правильно сделать постер Технологии поиска и хранение информации. CУБД Access
Технологии поиска и хранение информации. CУБД Access Архитектура персонального компьютера
Архитектура персонального компьютера Вычислительная техника и компьютерное моделирование в физике
Вычислительная техника и компьютерное моделирование в физике Кто живет в пруду?
Кто живет в пруду? Елементи статистичної фізики у комп’ютерному моделюванні
Елементи статистичної фізики у комп’ютерному моделюванні Основы программирования на Python. Лекция 2
Основы программирования на Python. Лекция 2 Инструменты разработки интернет-систем
Инструменты разработки интернет-систем Средства массовой информации и их виды
Средства массовой информации и их виды Информационные и коммуникационные технологии в журналистике
Информационные и коммуникационные технологии в журналистике Волоконно-оптические линии связи
Волоконно-оптические линии связи Презентация Электронная почта
Презентация Электронная почта Текстовый процессор MS Word
Текстовый процессор MS Word Перегрузка операторов
Перегрузка операторов Лекция 2016.3. Построение конфигурации. Дерево конфигурации
Лекция 2016.3. Построение конфигурации. Дерево конфигурации RusGameTactics (популярный летслейщик)
RusGameTactics (популярный летслейщик) Форматирование текста
Форматирование текста Ветвления. Разветвляющийся алгоритмический процесс
Ветвления. Разветвляющийся алгоритмический процесс Программирование на языке Python. Алгоритм и его свойства
Программирование на языке Python. Алгоритм и его свойства Технологии локальных сетей. (Тема 3)
Технологии локальных сетей. (Тема 3) Нұсқауларды қалыптастыру Топбасшылық және басқару. Дұрыс мінезді адамдар. Мотивация. Тиімді өзара әрекеттестік
Нұсқауларды қалыптастыру Топбасшылық және басқару. Дұрыс мінезді адамдар. Мотивация. Тиімді өзара әрекеттестік Информация и информационные процессы. Количество информации. Передача данных
Информация и информационные процессы. Количество информации. Передача данных Методы ООП. Введение в шаблоны. Тема 17
Методы ООП. Введение в шаблоны. Тема 17 Основы языка программирования. Язык С#
Основы языка программирования. Язык С# Изобретения, изменившие мир
Изобретения, изменившие мир Измерение информации
Измерение информации Таблиця маршрутизації
Таблиця маршрутизації Yandex Market
Yandex Market