Содержание
- 2. Общие понятия Система счисления — это способ записи (представления) чисел. Система счисления – совокупность приемов обозначения
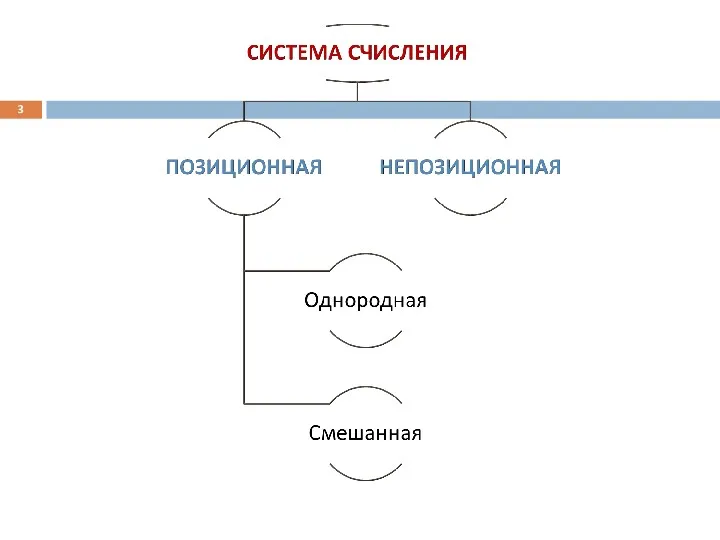
- 5. Непозиционные С/С С/С, алфавит которых содержит неограниченное количество символов, причем количественный эквивалент любой цифры постоянен, и
- 6. Унарная система счисления
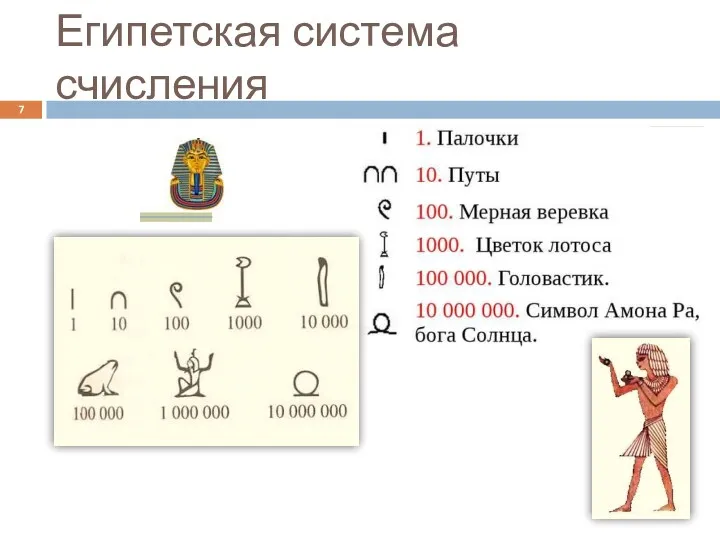
- 7. Египетская система счисления
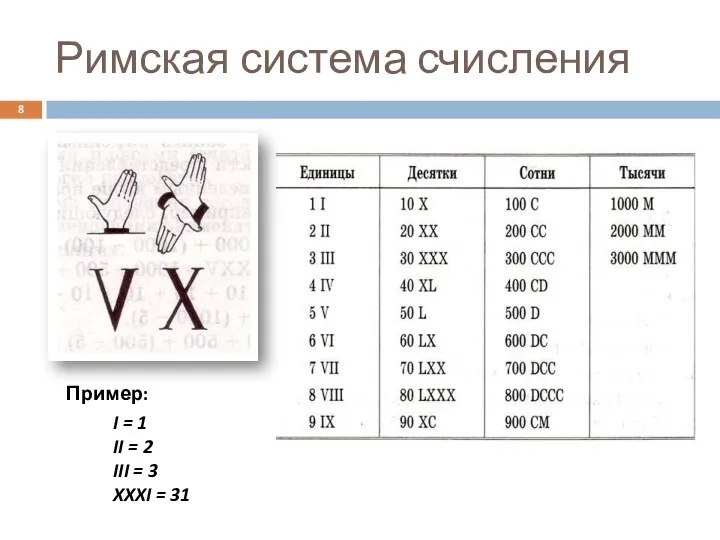
- 8. Римская система счисления Пример: I = 1 II = 2 III = 3 XXXI = 31
- 9. Славянская система счисления
- 10. Греческая система счисления
- 11. Позиционные С/С Позиционные – С/С, алфавит которых содержит ограниченное количество символов, причем значение каждой цифры в
- 12. Общие понятия Отдельную позицию в изображении числа принято называть разрядом, а номер позиции - номером разряда.
- 13. Позиционные система Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. Пример:
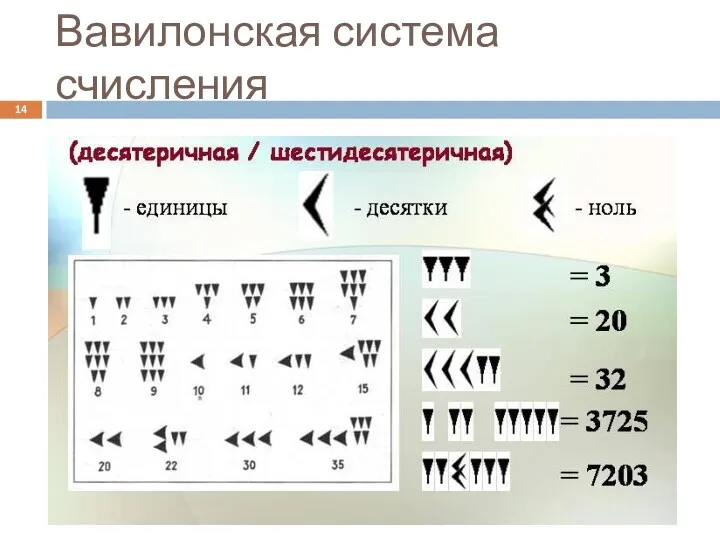
- 14. Вавилонская система счисления
- 15. Десятичная система счисления Алфавит 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
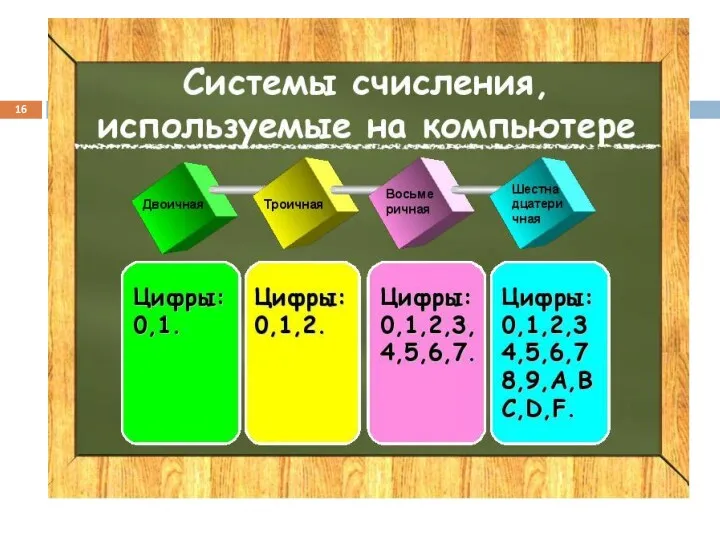
- 17. Двоичная система счисления Алфавит две цифры: 0, 1. Вес более старшего разряда в 2 раза больше.
- 18. «Есть 10 типов людей – одни понимают двоичную систему исчисления, а вторые нет»
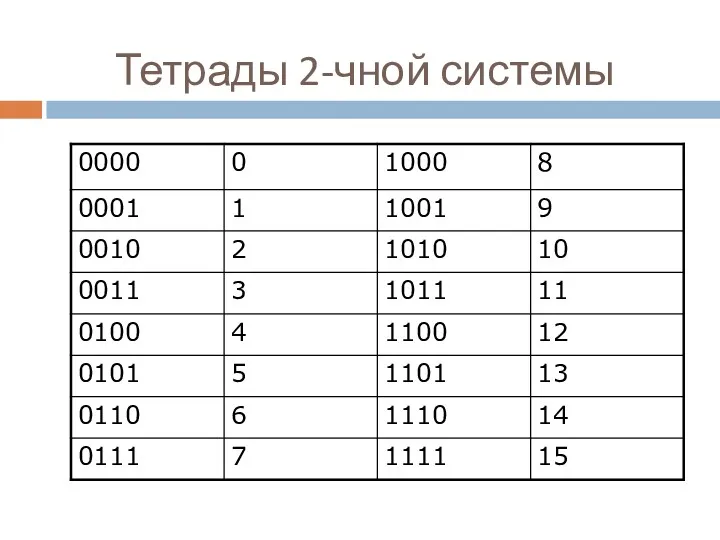
- 19. Тетрады 2-чной системы
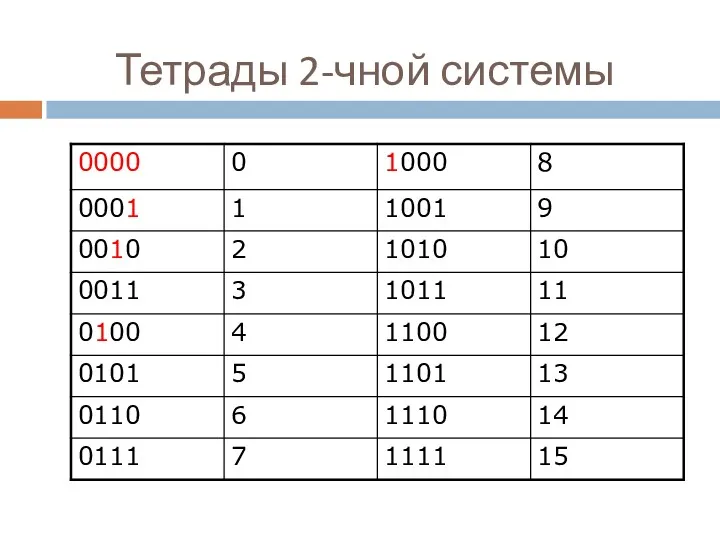
- 20. Тетрады 2-чной системы
- 21. Представление данных в ЭВМ Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он
- 22. Представление данных в ЭВМ Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со
- 23. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся,
- 24. 16-ричная система счисления Алфавит 16 символов: 0, 1, …, 8, 9, A, B, C, D, E,
- 25. Формы представления чисел Любое число А в позиционной С/С с основанием р может быть представлено в
- 26. Перевод из одних систем счисления в другие Общий принцип 1: чтобы перевести число в некоторую систему
- 27. Перевод из одних систем счисления в другие Общий принцип 2: Если основание одной системы - степень
- 28. Следствие теоремы: Правила перевода между системами P и Q Для перевода из Q-й в P-ю, необходимо
- 29. Пример 2 -> 16 : т.е. 16 = 2 4 , то собираем с конца двоичного
- 30. Пример: перевод из двоичной системы счисления в восьмеричную Возьмем двоичное число, разобьем его справа налево на
- 31. Перевод в десятичную систему счисления Перевод целого числа из M-ичной системы счисления в десятичную осуществляется путем
- 32. Перевод в десятичную С/С Вычисляем А(10) = an * Mn + an-1 * Mn-1 + ...
- 33. Примеры: Перевести 10101101 (2) → X10 10101101(2)=1*27+0*26+1*25+0*24+1*23+1*22+0*2+1 = Ответ: 173 10 Перевести 703(8) → X10 7038
- 34. Пример: перевод из двоичной в восьмеричную Возьмем двоичное число: 100111102, разобьем его справа налево на группы
- 35. Схема ГОРНЕРА позволяет минимизировать арифметические операции и исключить возведение в степень. Алгоритм: старшую цифру умножаем на
- 36. Пример:
- 37. Перевод из десятичной системы счисления Чтобы найти такое представление, необходимо: 1. разделить число нацело на M
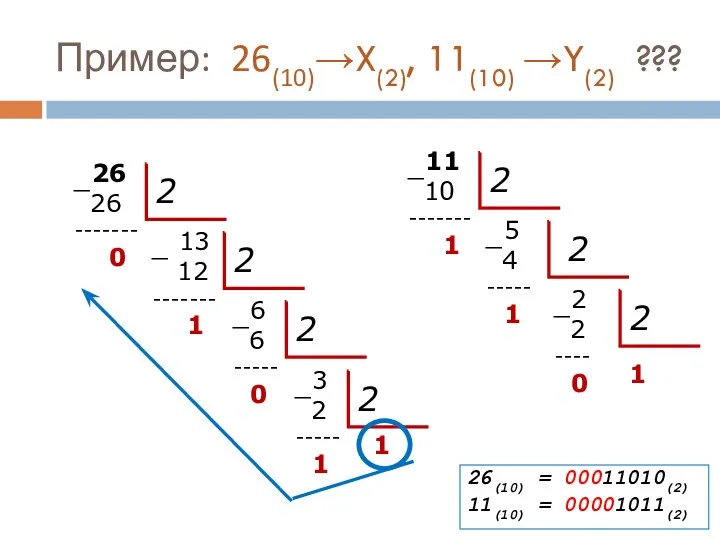
- 38. Пример: 26(10)→X(2), 11(10) →Y(2) ??? 26 ‾26 ------- 0 2 13 ‾ 12 ------- 1 2
- 39. Пример: 95(10)→Х(2) →Y(8) →Z(16) ?
- 40. Пример: Требуется перевести число 139(10) в 2-ную, 8-ную, 4-ную С/С. 1) 139/2 -> 69/ 34/ 17/
- 41. Перевод дробей Перевод правильной дроби из десятичной С/С в P-ичную осуществляется последовательным умножением на основание той
- 42. Примеры перевода правильной десятичной дроби 0.36: а) в двоичную б) в восьмеричную в) в шестнадцатеричную
- 43. Примеры:
- 44. Перевести 23.12510 →X2
- 45. Преобразование дроби из любой системы счисления в десятичную Преобразование осуществляется также, как и для целых частей,
- 46. Пример перевода дробей в 10 с/с
- 47. Замечания: Целые числа остаются целыми, а правильные дроби – правильными в любой системе счисления. Конечной десятичной
- 48. Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему (с помощью триад и
- 49. Двоичная система счисления широко используется в информатике и вычислительной технике, поэтому полезным оказывается знание первых шестнадцати
- 50. Задачка Учитель утверждает, что в его классе 100 учеников, при этом их них 32 мальчика и
- 51. двоично-десятичная система В такой системе каждая десятичная цифра кодируется определенной комбинацией цифр двоичной системы. Обозначение каждой
- 52. Литература для самостоятельной работы Гашков С.Б. Системы счисления и их применение. Серия: Библиотека «Математическое просвещение». //
- 54. Скачать презентацию











































 Выполнении вызова F(11)
Выполнении вызова F(11) Очередность работ при последовательной схеме технологического процесса
Очередность работ при последовательной схеме технологического процесса методическая копилка
методическая копилка TAHU. We are creative team
TAHU. We are creative team Архитектура компьютеров
Архитектура компьютеров Предметная область базы данных и ее модели
Предметная область базы данных и ее модели Хранение товаров и IT сервисы для электронной торговли
Хранение товаров и IT сервисы для электронной торговли Работа с базами данных PostgreSQL
Работа с базами данных PostgreSQL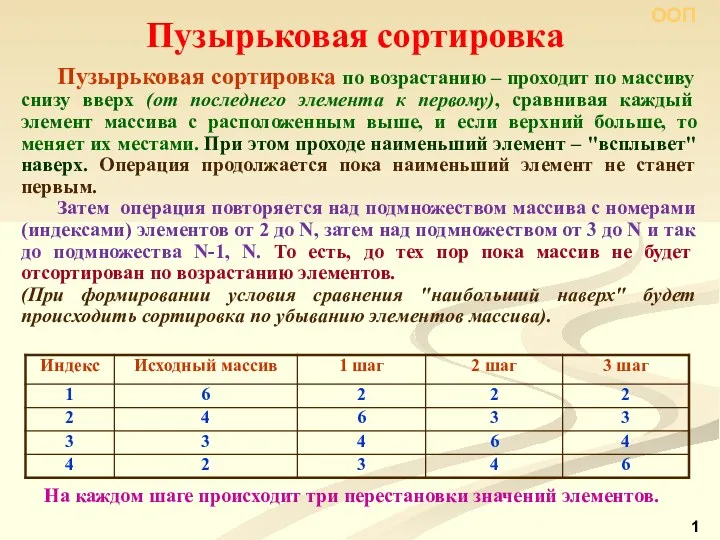 Пузырьковая сортировка
Пузырьковая сортировка Массивы в Pascal. Одномерные массивы
Массивы в Pascal. Одномерные массивы Организационные и технические способы и средства защиты информации. Шифровальная (криптографическая) защита информации
Организационные и технические способы и средства защиты информации. Шифровальная (криптографическая) защита информации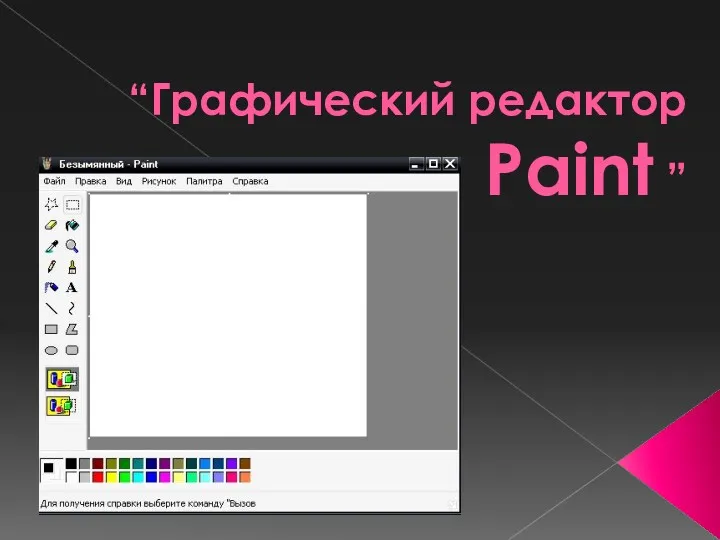 Графический редактор Paint
Графический редактор Paint Компьютерная графика
Компьютерная графика Организация ввода и вывода данных, 9 класс,Босова
Организация ввода и вывода данных, 9 класс,Босова Программирование на языке Python. Функции
Программирование на языке Python. Функции Сети мобильной связи нового поколения. Лекция 7. Подсистема IP-мультимедиа (IMS)
Сети мобильной связи нового поколения. Лекция 7. Подсистема IP-мультимедиа (IMS) Разработка урока информатики по теме Моделирование информационных процессов. Корреляционные зависимости
Разработка урока информатики по теме Моделирование информационных процессов. Корреляционные зависимости Внеклассное мероприятие по информатике
Внеклассное мероприятие по информатике Прикладные офисные пакеты
Прикладные офисные пакеты Носители документированной информации
Носители документированной информации Базы данных и системы управления базами данных
Базы данных и системы управления базами данных Политический SMM
Политический SMM Электронные таблицы
Электронные таблицы Единицы измерения информации
Единицы измерения информации Введение в криптографию. Основные понятия и определения. Виды криптосистем. Тема 2.1
Введение в криптографию. Основные понятия и определения. Виды криптосистем. Тема 2.1 Ensuring the security of information networks
Ensuring the security of information networks Решение задач ЕГЭ типа В2
Решение задач ЕГЭ типа В2 Основы информационной безопасности. Основные термины и определения. (Лекция 1)
Основы информационной безопасности. Основные термины и определения. (Лекция 1)