Содержание
- 2. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.
- 3. Действия над комплексными числами 1) Действия над комплексными числами, заданными в алгебраической форме а) Сложение комплексных
- 4. в) Умножение комплексных чисел Произведением комплексных чисел z1=x1+y1i и z2=x2+y2i называется комплексное число, определяемое равенством Z
- 5. г) Деление комплексных чисел Деление определяется как действие, обратное умножению. Частным двух комплексных чисел z1 и
- 6. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.
- 7. На практике вместо полученной формулы используют следующий прием: умножают числитель и знаменатель дроби на число, сопряженное
- 8. д) Возведение комплексного числа, заданного в алгебраической форме в n-ю степень Выпишем целые степени мнимой единицы:
- 9. е) Извлечение квадратного корня из комплексного числа Квадратным корнем из комплексного числа называется такое комплексное число,
- 10. Пример 4. Извлечем квадратный корень из комплексного числа z=5+12i. Решение. Обозначим квадратный корень из числа z
- 11. 2) Действия над комплексными числами, заданными в тригонометрической форме Рассмотрим два комплексных числа z1 и z2
- 12. б) Частное двух комплексных чисел Пусть заданы комплексные числа z1 и z2 ≠ 0. Рассмотрим частное
- 13. Пример . Даны два комплексных числа Найдите Решение. 1) Используя формулу . получаем Следовательно, 2) Используя
- 14. Найти произведение комплексных чисел: Действия над комплексными числами, заданными в тригонометрической форме
- 15. Найти частное комплексных чисел: Действия над комплексными числами, заданными в тригонометрической форме
- 16. Домашняя работа
- 17. Вычислите: 1. (2 + 3i) + (5 + i) = 2. (– 2 + 3i) –
- 18. При выполнении умножения можно использовать формулы: (a ± b)2 = a2 ± 2ab + b2, (a
- 20. Скачать презентацию

















 Занятия по математике Письмо для кота Матроскина в студии раннего творческого развития детей
Занятия по математике Письмо для кота Матроскина в студии раннего творческого развития детей Приёмы устных вычислений вида 240 умножить на 4
Приёмы устных вычислений вида 240 умножить на 4 Теорія ймовірностей. Основні поняття теорії ймовірностей (лекція 5)
Теорія ймовірностей. Основні поняття теорії ймовірностей (лекція 5) Способы определения понятий
Способы определения понятий Внеклассное мероприятие по математике: Своя игра
Внеклассное мероприятие по математике: Своя игра Свойства логарифмов
Свойства логарифмов Длина окружности и длина дуги окружности
Длина окружности и длина дуги окружности Застосування квадратного тричлена при розв'язуванні задач з параметром
Застосування квадратного тричлена при розв'язуванні задач з параметром Сумма и разность синусов и косинусов
Сумма и разность синусов и косинусов Комплексные числа и действия над ними
Комплексные числа и действия над ними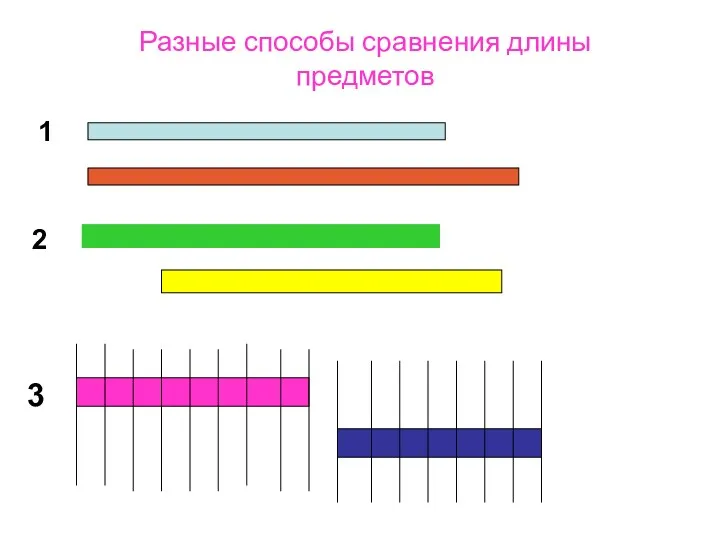 Измерение длины отрезка. Сантиметр.
Измерение длины отрезка. Сантиметр. Математическое описание случайных явлений
Математическое описание случайных явлений Математика в истории
Математика в истории Преобразование квадратных корней
Преобразование квадратных корней Решение дифференциальных уравнений в частных производных
Решение дифференциальных уравнений в частных производных Аксиомы стереометрии. Некоторые следствия из аксиом
Аксиомы стереометрии. Некоторые следствия из аксиом Задачи на построение (7 класс)
Задачи на построение (7 класс) Элементы комбинаторики. Примеры комбинаторных задач
Элементы комбинаторики. Примеры комбинаторных задач Соотношение между единицами измерения величин. Единицы длины
Соотношение между единицами измерения величин. Единицы длины Коэффициент. Упрощение выражений
Коэффициент. Упрощение выражений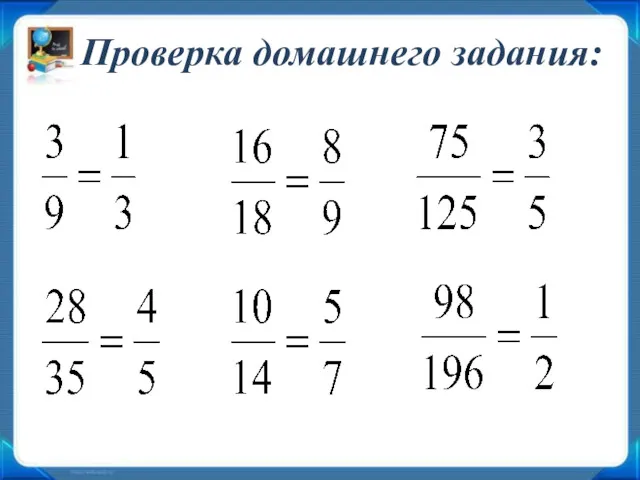 Приведение дробей общему знаменателю
Приведение дробей общему знаменателю Многогранники
Многогранники Наибольшее и наименьшее значения. Размах
Наибольшее и наименьшее значения. Размах Корень n-й степени из действительного числа. 11 класс
Корень n-й степени из действительного числа. 11 класс Занималка (устный счёт в пределах 10)
Занималка (устный счёт в пределах 10) Основное свойство пропорции
Основное свойство пропорции Повторим математику. Итоговое повторение курса 5 класса
Повторим математику. Итоговое повторение курса 5 класса Замечательные пределы
Замечательные пределы