Содержание
- 2. Если искомая функция зависит от одной переменной, то дифференциальное уравне- ние называется обыкновенным, если от не-
- 3. где - некоторая функция от переменных, при этом порядок старшей производной, входящей в запись уравнения, называется
- 4. Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования дифференциального уравнения. График решения диффуравнения называется
- 5. Частным решением дифференциального уравнения называется уравнение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных
- 6. Дифференциальные уравнения первого порядка Такие уравнения имеют вид: где - функция двух переменных, определенная на плоскости
- 7. 2. Уравнение Ищем решение в виде т.е. считаем, что переменная обозначает независимую переменную, а переменная -
- 8. 3. Если дифференциальное уравнение имеет вид то и, интегрируя, получаем: откуда Пример. Решить уравнение
- 9. Имеем или откуда Выполнив преобразования, получим Окончательно
- 10. Дифференциальное уравнение первого порядка называется уравнением с разделяю- щимися переменными, если оно может быть представлено в
- 11. Однородные дифференциальные уравнения первого порядка Дифференциальное уравнение первого порядка называется однородным, если оно может быть представлено
- 12. Пример. Решить уравнение введя переменную имеем
- 13. Выполнив преобразования, в итоге получим Дифференциальное линейное уравнение первого порядка Дифференциальное уравнение первого порядка называется линейным,
- 14. Пример. Решить уравнение Вначале решаем однородное уравнение где С – произвольная постоянная. Теперь возьмем функцию где
- 15. Подставляя значения в исходное выражение и произведя преобразования, получим Интегрируя, имеем где А – произвольная постоянная.
- 16. Дифференциальные уравнения второго порядка Дифференциальным линейным уравнением второго порядка называется уравнение вида: где - функции переменной
- 17. Дифференциальные уравнения второго порядка, допускающие понижение порядка В некоторых случаях решение дифференци- ального уравнения второго порядка
- 18. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами Линейной комбинацией функций с коэффициентами С1 и С2
- 19. Для решения линейных уравнений второго порядка с постоянными коэффициентами используется следующая теорема. Если - линейно независимые
- 20. Если характеристическое уравнение имеет действительные корни , причем , тогда общее решение уравнения, имеет вид: Если
- 21. где Метод Рунге – Кутта Связь между соседними значениями функции дает равенство: Для применения метода используется
- 22. Последовательно вычисляют: …….. и полагаем
- 23. Рассмотрим вопрос о выборе параметров Пусть Предполагаем, что а для некоторой функции По формуле Тэйлора имеем:
- 24. При Имеем: Погрешность на шаге:
- 25. На практике наиболее часто используют метод Рунге-Кутта с В этом случае расчетные формулы:
- 26. Погрешность рассмотренного метода Рунге-Кутта на шаге пропорциональна пятой степени шага. Пример. Методом Рунге-Кутта найти решение задачи
- 27. Далее находим: Вычислим
- 29. Скачать презентацию




















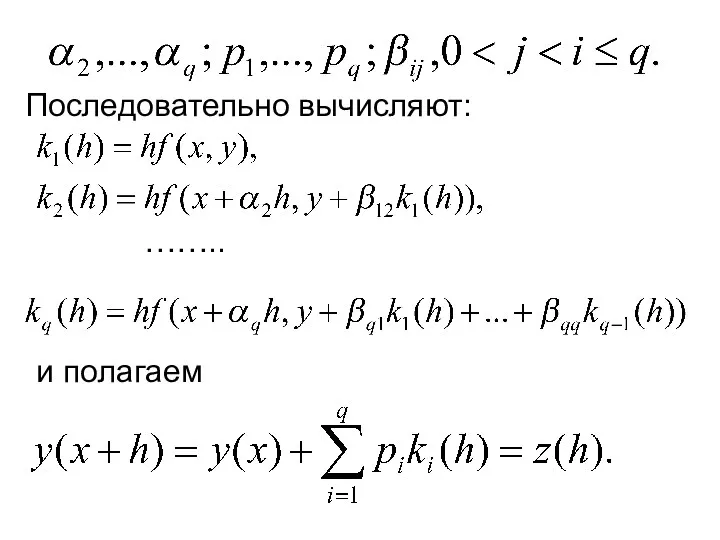

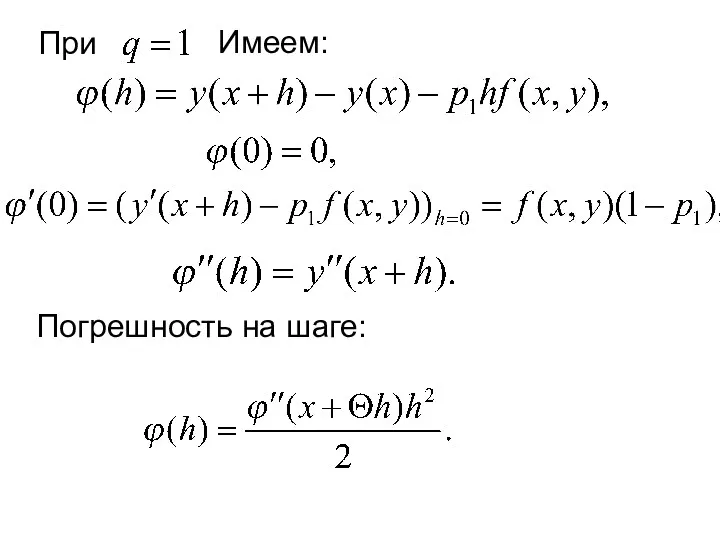



 Тест по теме: Векторы в пространстве. Сложение и вычитание векторов. Умножение вектора на число. Вариант 2
Тест по теме: Векторы в пространстве. Сложение и вычитание векторов. Умножение вектора на число. Вариант 2 Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника
Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника Дроби обыкновенные
Дроби обыкновенные Знаки < или >
Знаки < или > Приращение аргумента, приращение функции
Приращение аргумента, приращение функции Системы линейных алгебраических уравнений (СЛАУ)
Системы линейных алгебраических уравнений (СЛАУ) урок оценка знаний по математике
урок оценка знаний по математике Презентация к уроку математики во 2 классе по теме Периметр
Презентация к уроку математики во 2 классе по теме Периметр Математика в профессии технолог продукции общественного питания
Математика в профессии технолог продукции общественного питания Решение систем неравенств
Решение систем неравенств Равные треугольники. Высота, биссектриса, медиана. 7 класс
Равные треугольники. Высота, биссектриса, медиана. 7 класс Решение уравнений с десятичными дробями
Решение уравнений с десятичными дробями Делимость суммы и разности чисел. Урок 102
Делимость суммы и разности чисел. Урок 102 Теорема о пропорциональных отрезках. Теорема Фалеса 2
Теорема о пропорциональных отрезках. Теорема Фалеса 2 Перевод обыкновенной дроби в десятичную. Урок математики в 6 классе
Перевод обыкновенной дроби в десятичную. Урок математики в 6 классе Площади параллелограмма, треугольника и трапеции. Урок 20
Площади параллелограмма, треугольника и трапеции. Урок 20 Площадь прямоугольника. Свойства площадей
Площадь прямоугольника. Свойства площадей Синус, косинус, тангенс угла
Синус, косинус, тангенс угла Качество и средства измерений. (Лекция 2)
Качество и средства измерений. (Лекция 2) Умножение и деление.
Умножение и деление. Посчитаем. Примеры с ответами
Посчитаем. Примеры с ответами Конус
Конус Цилиндр. Понятие цилиндрической поверхности
Цилиндр. Понятие цилиндрической поверхности Деление десятичных дробей на натуральное число
Деление десятичных дробей на натуральное число Ондық бөлшек. Ондық бөлшектерді оқу және жазу
Ондық бөлшек. Ондық бөлшектерді оқу және жазу Нахождение числа по его дроби. 6 класс
Нахождение числа по его дроби. 6 класс Урок по теме Сложение и вычитание двузначных чисел в столбик с элементами критического мышления
Урок по теме Сложение и вычитание двузначных чисел в столбик с элементами критического мышления Взаимно обратные числа. Задание для устного счета
Взаимно обратные числа. Задание для устного счета