Содержание
- 2. Комбинаторика - раздел математики, посвященный решению задач выбора и расположения элементов некоторого, как правило, конечного множества
- 3. Множество Всякая совокупность элементов произвольного рода, обладающая некоторым общим свойством, образует множество (соединение).
- 4. Примеры множеств: множество всех действительных чисел, множество натуральных чисел, множество всех студентов данного университета, множество парт
- 5. Множество считается определенным, если указаны все его элементы или указано их общее свойство. Множества, содержащие конечное
- 6. Множество, состоящее из n элементов, называется упорядоченным, если каждому элементу этого множества поставлено в соответствие натуральное
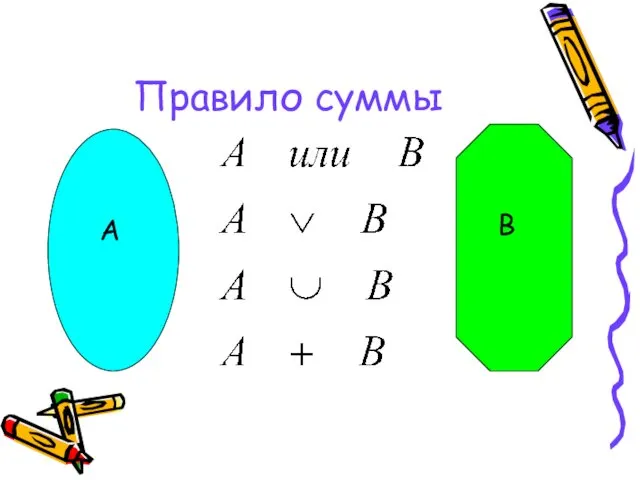
- 7. Правило суммы Пусть некоторый предмет А может быть выбран m способами, а другой предмет В может
- 8. Правило суммы
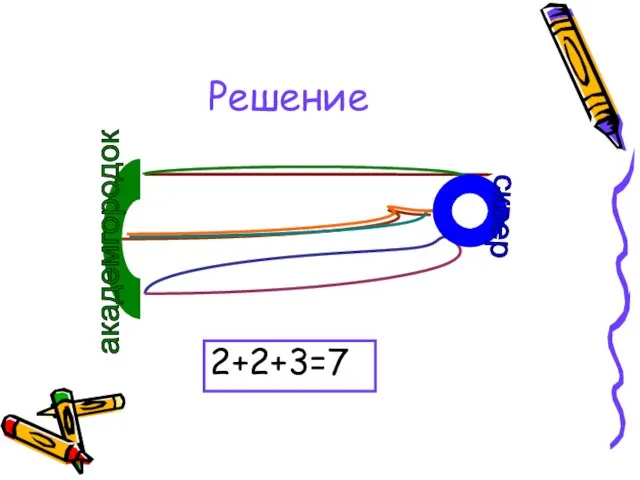
- 9. Задача 1 От сквера Кирова до академгородка можно проехать через Ангарский мост, плотину и новый мост.
- 10. Решение 2+2+3=7
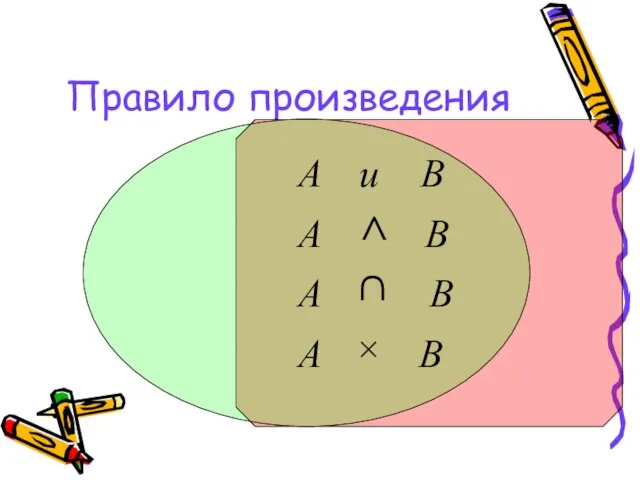
- 11. Правило произведения Пусть некоторый предмет А может быть выбран m способами, а другой предмет В может
- 12. Правило произведения
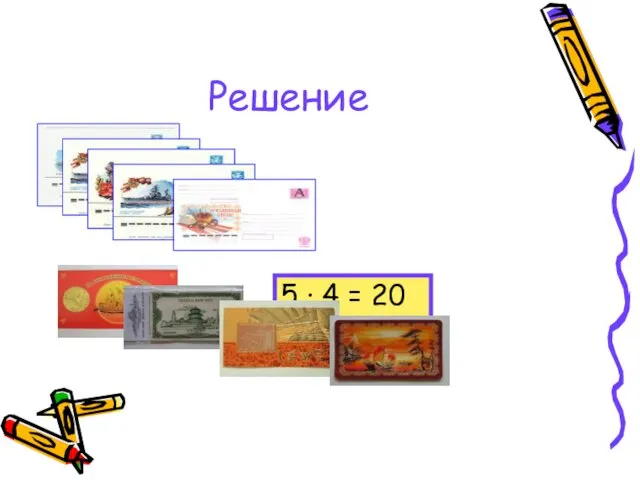
- 13. Задача 2 В киоске продают 5 видов конвертов и 4 вида открыток. Сколькими способами можно купить
- 14. Решение 5 · 4 = 20
- 15. Задача 3 Сколькими способами можно выбрать гласную и согласную буквы из слова КОНВЕРТ?
- 16. Решение Гласную можно выбрать двумя способами. Согласную — пятью способами. Ответ. 2 · 5 = 10.
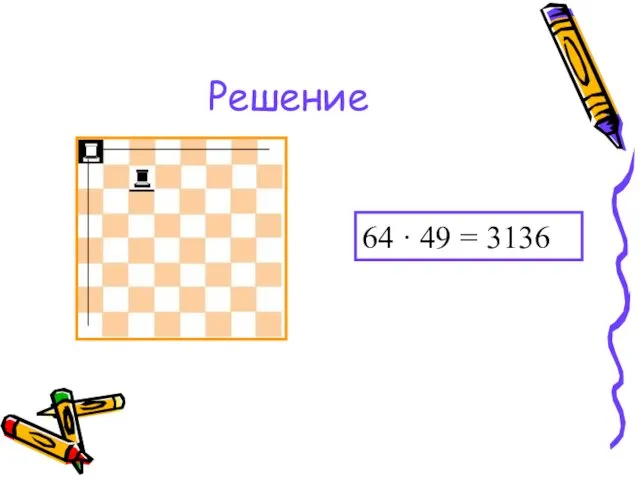
- 17. Задача 4 Сколькими способами можно поставить на шахматную доску белую и чёрную ладьи так, чтобы они
- 18. Решение 64 · 49 = 3136
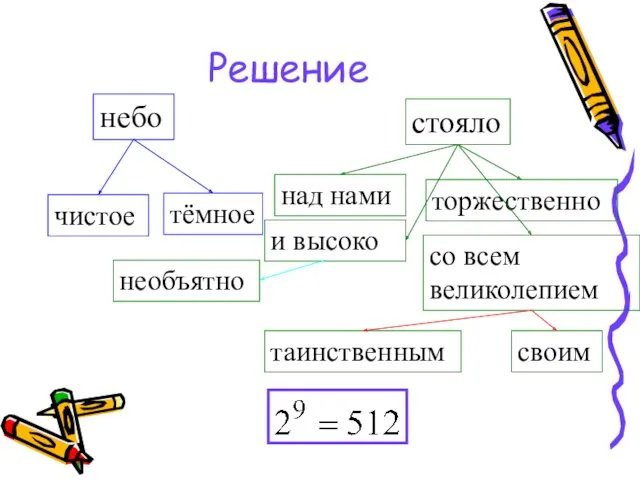
- 19. Задача 5 «Тёмное , чистое небо торжественно и необъятно высоко стояло над нами со всем своим
- 20. Решение небо стояло тёмное чистое торжественно и высоко над нами со всем великолепием таинственным своим необъятно
- 21. Задача 6 От Братска до Иркутска можно добраться поездом, самолётом, автобусом, теплоходом. Из Иркутска до Листвянки
- 22. Решение Б И Л
- 23. Задача 7 У двух начинающих коллекционеров по 20 марок и по 10 значков. Честным обменом называется
- 24. Решение
- 25. Задача 8 На глобусе проведены 17 параллелей и 24 меридиана. На сколько частей разделена поверхность глобуса?
- 26. Решение Меридианы делят глобус на 24 части, а параллели делят каждую часть ещё на 17 +
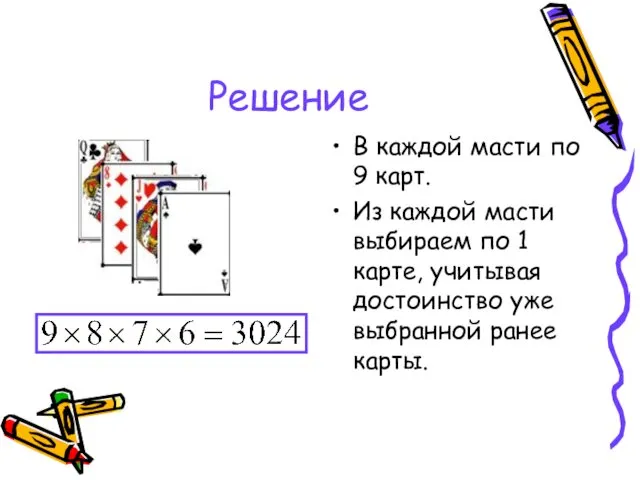
- 27. Задача 9 Сколькими способами из колоды (36 карт) можно выбрать 4 карты разных мастей и достоинств?
- 28. Решение В каждой масти по 9 карт. Из каждой масти выбираем по 1 карте, учитывая достоинство
- 29. Факториал произведение всех натуральных чисел от 1 до n включительно (читается n–факториал). n! = 1•2•3•…•n Замечание:
- 30. Перестановки Число различных способов, которыми может быть упорядочено данное множество, состоящее из n элементов, называется числом
- 31. Перестановки без повторений
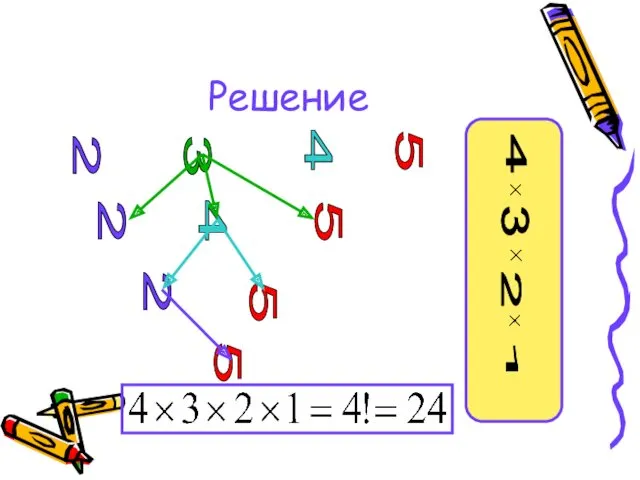
- 32. Задача 10 Сколько существует четырехзначных чисел, в записи которых цифры 2, 3, 4, 5 встречаются ровно
- 33. Решение 2 3 4 5 2 4 5 2 5 5 4 3 2 1
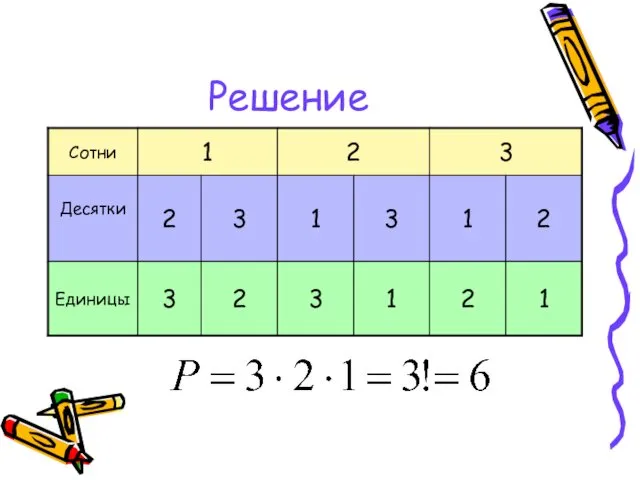
- 34. Задача 11 Сколько трёхзначных чисел можно получить из цифр 1,2,3, если цифры в числе не повторяются?
- 35. Решение
- 36. Перестановки с повторениями Пусть имеются предметы k различных типов. Сколько перестановок можно сделать из n1 элементов
- 37. Перестановки с повторениями
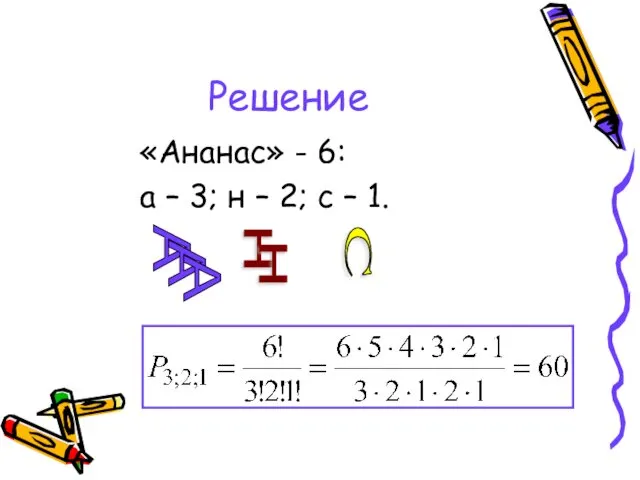
- 38. Задача 12 Сколькими способами можно переставить буквы слова «ананас», так, чтобы получались разные «слова»? Смысл «слов»
- 39. Решение «Ананас» - 6: а – 3; н – 2; с – 1. А А А
- 40. Задача 13 К Маше пришли 7 подружек. Сколькими способами можно рассадить 8 человек за столом?
- 41. Решение
- 42. Задача 14 8 девушек водят хоровод. Сколькими способами они могут встать в круг?
- 43. Решение Девушки могут перемещаться по кругу. Число перестановок уменьшается в 8 раз. Ответ: 7!
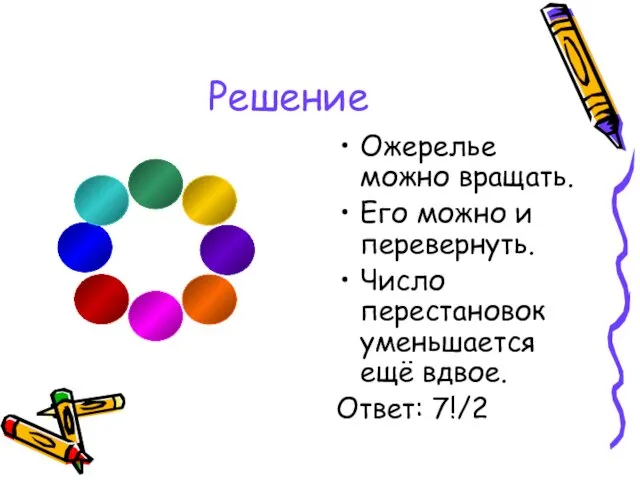
- 44. Задача 15 Сколько ожерелий можно составить из 8 различных бусин?
- 45. Решение Ожерелье можно вращать. Его можно и перевернуть. Число перестановок уменьшается ещё вдвое. Ответ: 7!/2
- 46. Размещения Число упорядоченных k элементных подмножеств множества из n элементов называется числом размещений из n элементов
- 47. Размещения
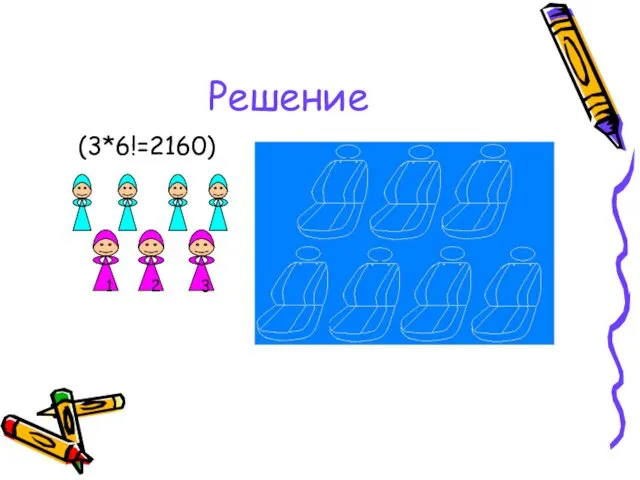
- 48. Задача В машине 7 мест, включая водительское. Поедут 7 человек. Сколько существует способов распределения пассажиров по
- 49. Решение (3*6!=2160)
- 50. Задача У людоеда в подвале томятся 25 пленников. Сколькими способами он может выбрать трех из них
- 51. Решение
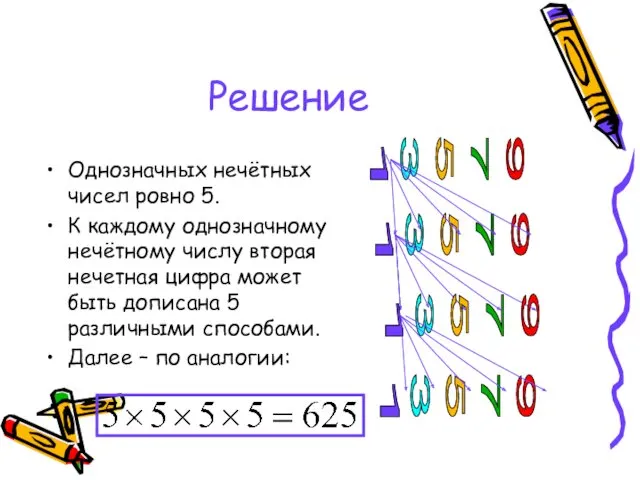
- 52. Задача Сколько существует 4-значных чисел, в записи которых встречаются только нечетные цифры?
- 53. Решение Однозначных нечётных чисел ровно 5. К каждому однозначному нечётному числу вторая нечетная цифра может быть
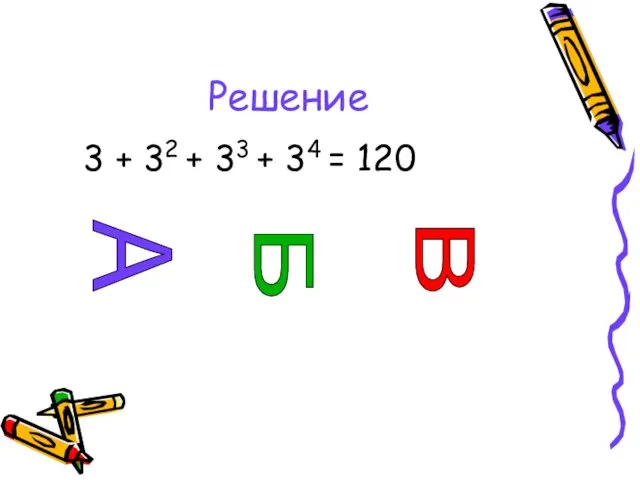
- 54. Задача Алфавит племени Мумбо-Юмбо состоит из трех букв А, Б и В. Словом является любая последовательность,
- 55. Решение 3 + 32 + 33 + 34 = 120 А В Б
- 56. Сочетания Если из n элементов составлять группы по m элементов в каждой, не обращая внимания на
- 57. Сочетания
- 58. Задача. В городе проводится первенство по футболу. Сколько в нем состоится матчей, если участвуют 12 команд?
- 59. Решение.
- 60. Задача. В группе 10 стрелков, из них 6 снайперов. Для выполнения боевой задачи нужно отобрать 5
- 61. Решение Не меньше 4 – это значит, что снайперов должно быть либо 4, либо 5.4 снайпера
- 62. Задача. В классе 24 ученика, из них 8 отличников. Нужно выбрать 12 человек так, чтобы среди
- 63. Свойства сочетаний
- 64. Решить систему уравнений:
- 65. Решение
- 66. Треугольник Паскаля Треугольник Паскаля является одной из наиболее известных и изящных числовых схем во всей математике.
- 67. Треугольник Паскаля Эта треугольная таблица была известна задолго до 1665 года - даты выхода в свет
- 68. Изображен треугольник на иллюстрации книги "Яшмовое зеркало четырех элементов" китайского математика Чжу Шицзе, выпущенной в 1303
- 69. Построение треугольника Паскаля Треугольник Паскаля - это бесконечная числовая таблица "треугольной формы", в которой на вершине
- 70. Свойства строк Сумма чисел n-й строки Паскаля равна (потому что при переходе от каждой строки к
- 71. Свойства строк Все строки треугольника Паскаля симметричны (потому что при переходе от каждой строки к следующей
- 72. Свойства строк Каждый член строки треугольника Паскаля с номером n тогда и только тогда делится на
- 73. Нахождение элемента треугольника Каждое число в треугольнике Паскаля можно определить тремя способами: где n - номер
- 75. Скачать презентацию









































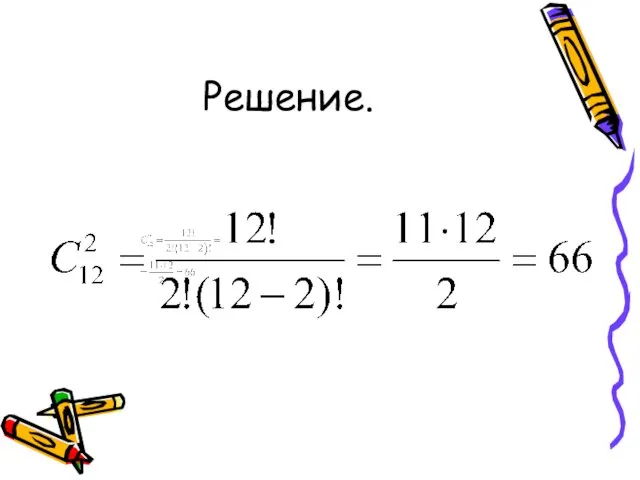



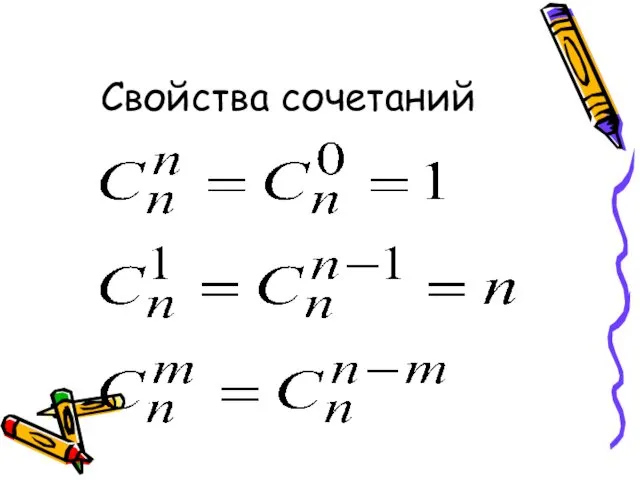










 Площадь сферы и объем шара
Площадь сферы и объем шара Составные задачи на нахождение остатка
Составные задачи на нахождение остатка Чтение графиков, диаграмм, таблиц
Чтение графиков, диаграмм, таблиц Теоретическая модель жизни пчелиных колоний
Теоретическая модель жизни пчелиных колоний Исследование функций и построение графиков с помощью производной
Исследование функций и построение графиков с помощью производной Свойства действий с рациональными числами
Свойства действий с рациональными числами Ряды динамики и их применение в анализе социально-экономических явлений
Ряды динамики и их применение в анализе социально-экономических явлений Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции
Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции открытый урок по математике Объём прямоугольного параллелепипеда 3 класс
открытый урок по математике Объём прямоугольного параллелепипеда 3 класс Математический диктант 4
Математический диктант 4 Правильные многогранники (тела Платона)
Правильные многогранники (тела Платона) презентация на тему переместительное свойство сложения
презентация на тему переместительное свойство сложения Сравнение дробей
Сравнение дробей Презентация к уроку математики в 1 классе по теме Состав числа 10.
Презентация к уроку математики в 1 классе по теме Состав числа 10. 3 ступень. Математика. Таблица умножения
3 ступень. Математика. Таблица умножения Острые и тупые углы. 2 класс. Программа Школа 2100.
Острые и тупые углы. 2 класс. Программа Школа 2100. Умножение на 1 и на 0
Умножение на 1 и на 0 Решение систем уравнений способом сложения
Решение систем уравнений способом сложения Урок Сложение двузначных чисел в столбик, технология проблемного обучения
Урок Сложение двузначных чисел в столбик, технология проблемного обучения Лекция 2 по статистике. Основные категории и понятия статистики
Лекция 2 по статистике. Основные категории и понятия статистики Множества. Операции над множествами
Множества. Операции над множествами Тест по математике +3, -3 , 1 класс.
Тест по математике +3, -3 , 1 класс. Прямая пропорциональность
Прямая пропорциональность презентация к уроку Виды треугольников
презентация к уроку Виды треугольников Порівняння раціональних чисел. Математика. 6 клас
Порівняння раціональних чисел. Математика. 6 клас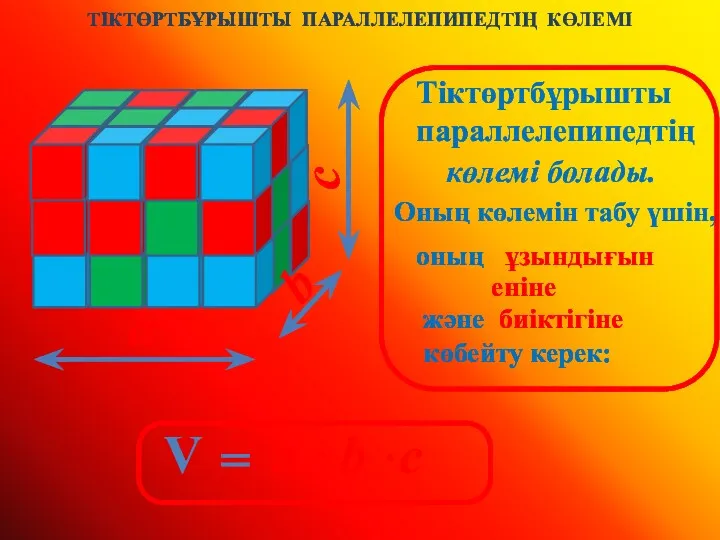 Тіктөртбұрышты параллелепипедтің көлемі
Тіктөртбұрышты параллелепипедтің көлемі Урок математики в 4 классе Шар и круг
Урок математики в 4 классе Шар и круг Окружность. Дети. Своя игра
Окружность. Дети. Своя игра