Слайд 2

Глава 3.
Линейная алгебра
Слайд 3
Слайд 4

Определение.
Матрицей размера (или
числовой матрицей) называется
прямоугольная таблица,
образованная из
mn чисел и
состоящая из m строк и n столбцов
Слайд 5

Матрицы записывают в виде:
Слайд 6
![или более кратко: [aij], (aij), соответственно.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-5.jpg)
или более кратко: [aij], (aij),
соответственно.
Слайд 7

Числа aij называются
элементами матрицы; ai1, ai2, …, ain
–
элементы i-й строки;
a1j, a2j, …, amj – элементы
j-го столбца. Матрицы обозначают:
A, B, C, … .
Слайд 8
![Две матрицы A = [aij] и B = [bij] размера](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-7.jpg)
Две матрицы A = [aij] и B = [bij]
размера
называются равными,
если aij = bij пишут:
A = B.
Слайд 9

Нулевая матрица
(обозначается О) – матрица размера
все элементы которой
равны
нулю.
Слайд 10

Матрица, состоящая из одной
строки, называется матрицей-
строкой, а состоящая из
одного
столбца – матрицей-столбцом.
Трапециевидной матрицей
называется матрица вида
Слайд 11

где aii ≠ 0
Слайд 12

Прямоугольной называется
матрица размера у которой
m ≠ n.
Матрица
размера называется
квадратной порядка n.
Слайд 13
![Главной диагональю квадратной матрицы A = [aij] порядка n называется](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-12.jpg)
Главной диагональю квадратной
матрицы A = [aij] порядка n
называется
совокупность элементов
aii а побочной диагональю –
совокупность элементов ai n–i+1
Слайд 14

Диагональной называется
квадратная матрица, у которой все
элементы, расположенные вне
главной диагонали, равны нулю.
Слайд 15

Единичная матрица
(обозначается Е) – диагональная
матрица, у которой все
элементы,
стоящие на главной диагонали,
равны единице.
Слайд 16

Квадратная матрица называется
треугольной, если все ее элементы,
расположенные по
одну сторону от
главной диагонали, – нули.
Слайд 17

Если элементами матрицы
являются функции, то матрица
называется функциональной.
Слайд 18

Слайд 19
§ 2. Операции
над матрицами
Слайд 20
![Определение. Суммой матриц A = [aij] и B = [bij]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-19.jpg)
Определение.
Суммой матриц A = [aij] и B = [bij]
размеров
называется матрица
A + B = [aij + bij] размера
Слайд 21
![Определение. Произведением матрицы A = [aij] размера на число λ называется матрица λA = [λaij] размера](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-20.jpg)
Определение.
Произведением матрицы A = [aij]
размера на число λ
называется
матрица λA = [λaij]
размера
Слайд 22

Матрица –A = (–1)A называется
противоположной матрице A.
Разностью матриц
A и B
называется матрица A – B = A + (–B).
Слайд 23
![Определение. Произведением матрицы A = [aik] размера на матрицу B](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-22.jpg)
Определение.
Произведением матрицы A = [aik]
размера на матрицу B =
[bkj]
размера называется матрица
AB = [ai1b1j + ai2b2j + ai3b3j +…+ ainbnj]
размера
Слайд 24

Операция произведения матриц
A и B определена для согласованных
матриц, т.е.
когда количество
столбцов матрицы A равно
количеству строк матрицы B.
Слайд 25

Если AB = BA, то матрицы A и B
называются
перестановочными (или
коммутирующими).
Слайд 26

Определение.
k-й степенью квадратной
матрицы A называется матрица Ak
такая, что
По
определению, A0 = E.
Слайд 27

Операции над матрицами
обладают свойствами:
1) A + B =
B + A,
2) (A + B) + C = A + (B + C),
3) λ(μA) = (λμ)A
4) (λ + μ)A = (λA + μA)
Слайд 28
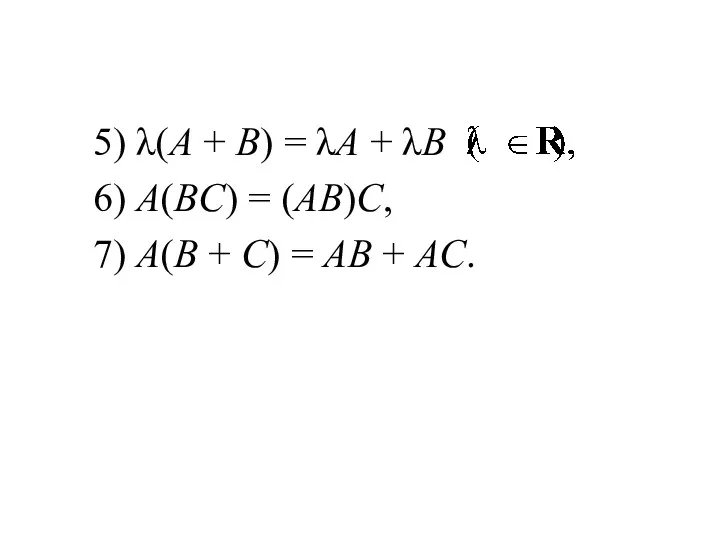
A(BC) = (AB)C,
7) A(B + C) = AB + AC.
Слайд 29
![Определение. Матрицей, транспонированной по отношению к матрице A = [aij]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-28.jpg)
Определение.
Матрицей, транспонированной по
отношению к матрице A = [aij]
размера
называется матрица
AT = [aji] размера
Слайд 30

Переход от A к AT называется
транспонированием.
Слайд 31

Операция транспонирования
обладает свойствами:
1) (AT)T = A,
2) (λA)T
= λAT
3) (A + B)T = AT + BT,
4) (AB)T = BTAT.
Слайд 32

Слайд 33
Слайд 34
![Если A = [a11], то определителем первого порядка называется число a11.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-33.jpg)
Если A = [a11], то определителем
первого порядка называется число
a11.
Слайд 35

Определение.
Если то
определителем второго порядка
называется число
Слайд 36
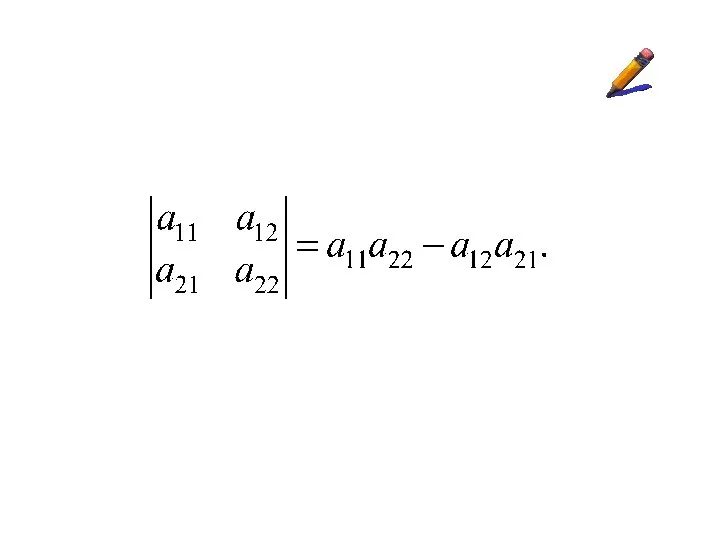
Слайд 37

Определение.
Если то
определителем третьего порядка
называется число
Слайд 38
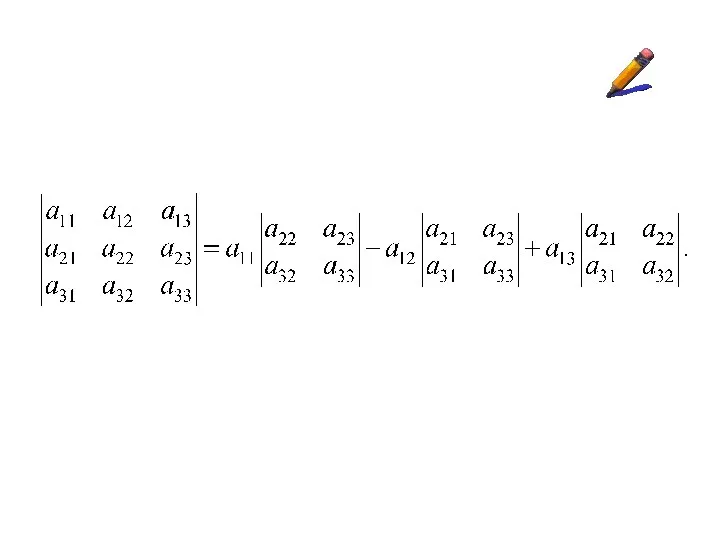
Слайд 39

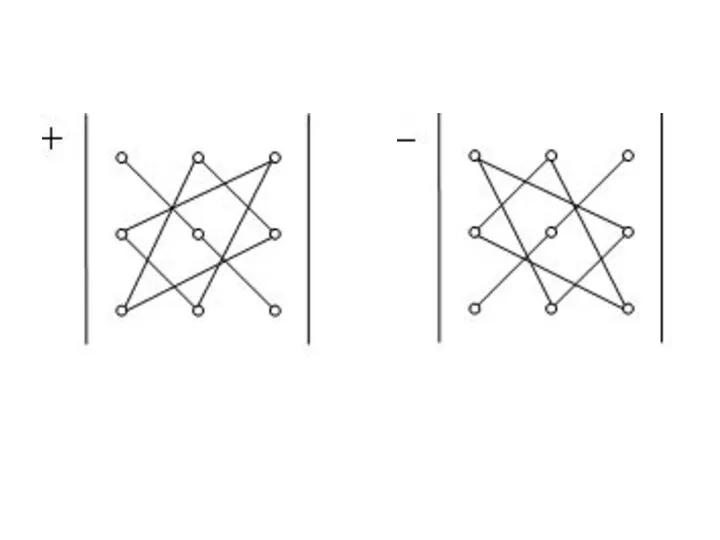
Для вычисления определителя
третьего порядка можно
использовать правило
треугольников:
Слайд 40
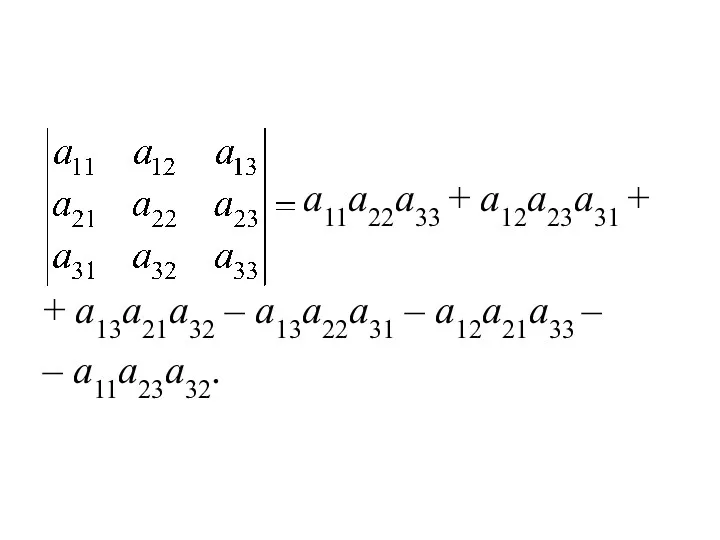
a11a22a33 + a12a23a31 +
+ a13a21a32 – a13a22a31 – a12a21a33
–
– a11a23a32.
Слайд 41
Слайд 42
![Если A = [aij] то определитель n-го порядка записывают в виде](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-41.jpg)
Если A = [aij] то
определитель n-го порядка
записывают в
виде
Слайд 43

где aij называются
элементами определителя.
Слайд 44

Определитель матрицы A
обозначают: Δ, detA, |A|.
Слайд 45

Определение.
Минором Mij элемента aij
определителя n-го порядка (n > 1)
называется определитель (n –1)-го
порядка, полученный из исходного
вычеркиванием i-й строки и j-го
столбца.
Слайд 46

Определение.
Алгебраическим дополнением Aij
элемента aij определителя n-го
порядка называется число
Aij
= (–1)i+jMij.
Слайд 47
![Определитель n-го порядка матрицы A = [aij] можно вычислять: 1) путем разложения по элементам i-й строки:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-46.jpg)
Определитель n-го порядка
матрицы A = [aij] можно вычислять:
1)
путем разложения по
элементам i-й строки:
Слайд 48

2) путем разложением по
элементам j-го столбца:
Слайд 49

Определители обладают
следующими свойствами:
1) если все элементы какого-
либо ряда
определителя равны
нулю, то определитель равен
нулю;
Слайд 50

2) при перестановке двух строк
(столбцов) определитель изменит
знак на
противоположный;
3) определитель, содержащий две
одинаковых строки (столбца), равен
нулю;
Слайд 51

4) если все элементы некоторой
строки (столбца) определителя
умножить на
число k то
исходный определитель умножится
на это число;
Слайд 52

5) если соответствующие
элементы двух строк (столбцов)
определителя пропорциональны, то
он равен нулю;
Слайд 53

6) определитель не изменится,
если к элементам какой-либо строки
(столбца)
прибавить
соответствующие элементы другой,
умноженной на одно и то же число;
Слайд 54

Справедливы формулы:
|AB| = |A||B|,
|An| = |A|n
|AT| =
|A|.
Слайд 55

Слайд 56
Слайд 57

Квадратная матрица А называется
невырожденной (или неособенной)
если |A| ≠
0. В противном случае A –
вырожденная (или особенная).
Слайд 58

Определение.
Матрица A–1 называется обратной
матрицей для квадратной матрицы
А, если
AA–1 = A–1A = E,
где E – единичная матрица.
Слайд 59

Теорема.
Матрица А имеет обратную тогда
и только тогда, когда матрица
А –
невырожденная.
Слайд 60
![Если A = [aij] то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-59.jpg)
Слайд 61

где |A| – определитель матрицы А,
Aij – алгебраические дополнения
элементов aij
матрицы А.
Слайд 62

Обратная матрица обладает
свойствами:
1)
2) (A–1)–1 = A,
Слайд 63
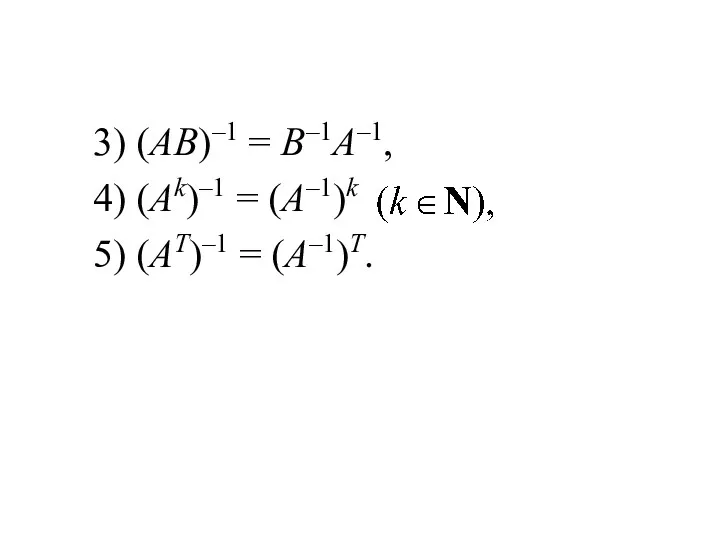
3) (AB)–1 = Β–1Α–1,
4) (Ak)–1 = (A–1)k
5)
(AT)–1 = (A–1)T.
Слайд 64

Слайд 65
Слайд 66

Определение.
Рангом матрицы называется
наивысший порядок отличных от
нуля ее миноров.
Ранг матрицы A обозначают:
r(A), rA, rank A.
Слайд 67

Базисным минором матрицы
называется любой отличный от нуля
минор порядка
r = r(A).
Слайд 68

Метод окаймляющих миноров.
Если в матрице A найден ненулевой
минор
Mk порядка k а все
окаймляющие его миноры (k +1)-го
порядка равны нулю, то ранг
матрицы A равен k.
Слайд 69

Слайд 70

§ 6. Системы линейных алгебраических уравнений
Слайд 71

Определение.
Системой m линейных
алгебраических уравнений с n
неизвестными x1, x2,
…, xn
называется система вида
Слайд 72
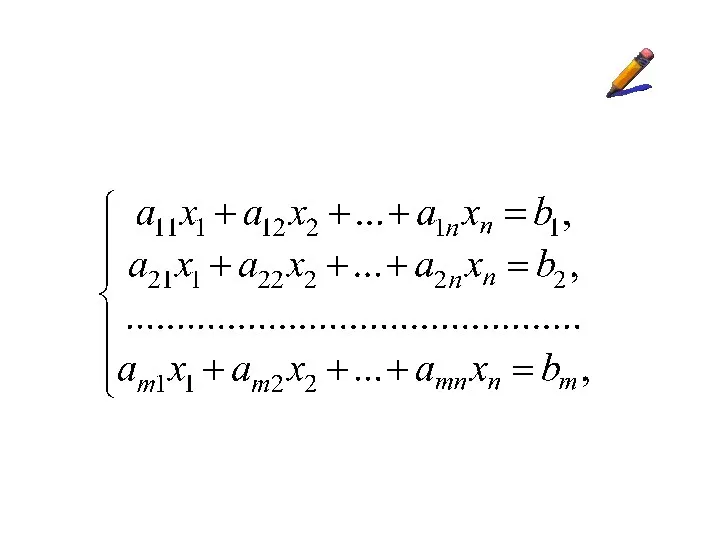
Слайд 73

где aij –
коэффициенты системы; bi –
свободные члены;
Слайд 74

Решением системы называется
совокупность n значений
неизвестных, удовлетворяющих
одновременно всем
уравнениям
системы.
Слайд 75

Система уравнений называется
совместной, если она имеет хотя бы
одно
решение. В противном случае
система называется несовместной.
Слайд 76

Система называется
определенной, если она имеет
единственное решение.
Слайд 77

Решить систему – значит
определить, совместна она или нет,
и
в случае совместности найти
множество всех ее решений.
Слайд 78

Матрица
называется матрицей (или основной
матрицей) системы.
Слайд 79

Матрица
называется расширенной матрицей
системы
Слайд 80

Теорема Кронекера – Капелли.
Система линейных алгебраических
уравнений совместна тогда и
только
тогда, когда r(A) = r([A|B]).
Слайд 81

Определение.
Определителем системы n
линейных уравнений с n
неизвестными называется
определитель
Δ матрицы этой
системы.
Слайд 82

Если Δ ≠ 0, то система имеет
единственное решение и
называется
невырожденной.
Если Δ = 0, то система не имеет
решения или имеет бесконечное
множество решений и называется
вырожденной.
Слайд 83

Для решения невырожденной
системы используют метод Крамера
и метод обратной
матрицы.
Слайд 84

Метод Крамера. Необходимо:
1) вычислить определитель Δ
системы;
2) в
определителе Δ заменить
поочередно i-й столбец столбцом
свободных членов и вычислить
соответствующие определители Δi ;
Слайд 85

3) вычислить значения
x1, x2, …, xn по формулам Крамера:
4) записать
решение (x1, x2,…, xn).
Слайд 86

Метод обратной матрицы.
Необходимо:
1) записать систему в матричном
виде:
AX = B, где A – матрица
системы, X – матрица-столбец
неизвестных, B – матрица-столбец
свободных членов;
Слайд 87

2) решить матричное уравнение
X = A–1B;
3) записать
решение (x1, x2,…, xn).
Слайд 88

Основным методом решения
произвольных систем является
метод Гаусса. Он базируется
на
понятии элементарных
преобразований строк матрицы
системы.
Слайд 89

Элементарными
преобразованиями строк матрицы
называются:
1) перестановка строк;
2) умножение
строки на одно и то
же число λ (λ ≠ 0);
Слайд 90

3) прибавление к строке матрицы
другой строки, умноженной на
некоторое
число.
В результате элементарных
преобразований строк матрицы A
получают эквивалентную матрицу
B; пишут: A ~ B.
Слайд 91

Метод Гаусса. Необходимо:
1) записать расширенную
матрицу системы;
2) с
помощью элементарных
преобразований строк расширенной
матрицы свести матрицу системы к
треугольной или трапециевидной;
Слайд 92

3) для преобразованной таким
образом расширенной матрицы
записать соответствующую систему
уравнений;
4) решить полученную систему
начиная с последнего уравнения;
5) записать решение (x1, x2,…, xn).




![или более кратко: [aij], (aij), соответственно.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-5.jpg)

![Две матрицы A = [aij] и B = [bij] размера](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-7.jpg)




![Главной диагональю квадратной матрицы A = [aij] порядка n называется](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-12.jpg)






![Определение. Суммой матриц A = [aij] и B = [bij]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-19.jpg)
![Определение. Произведением матрицы A = [aij] размера на число λ называется матрица λA = [λaij] размера](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-20.jpg)

![Определение. Произведением матрицы A = [aik] размера на матрицу B](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-22.jpg)




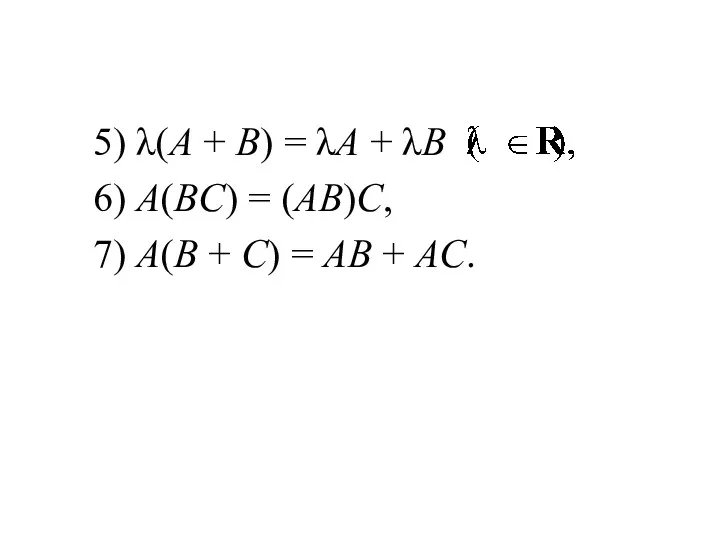
![Определение. Матрицей, транспонированной по отношению к матрице A = [aij]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-28.jpg)




![Если A = [a11], то определителем первого порядка называется число a11.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-33.jpg)

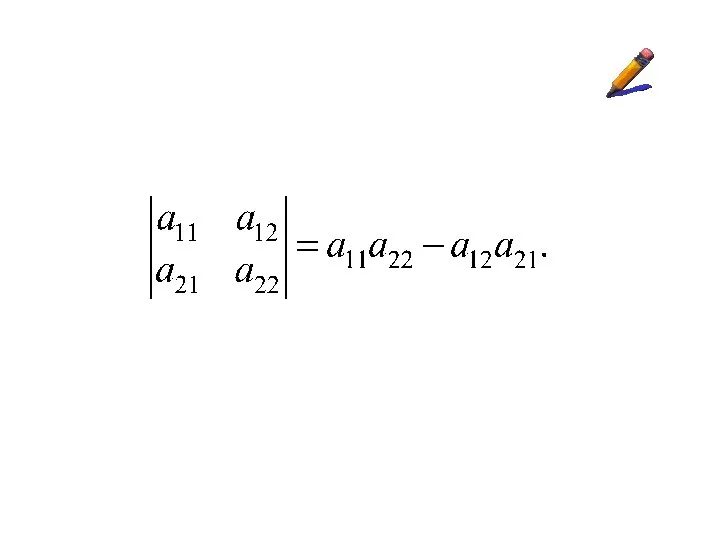

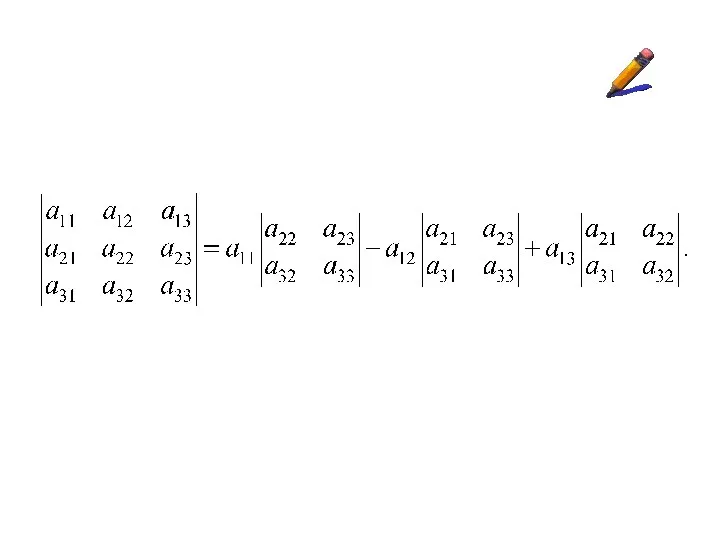

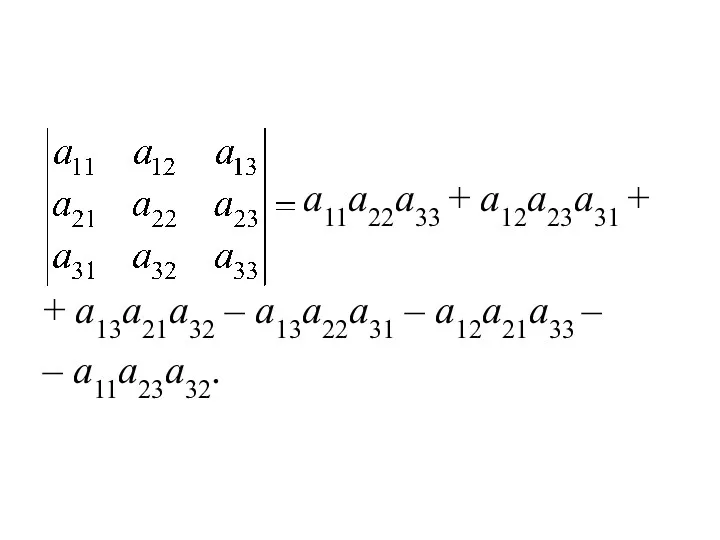

![Если A = [aij] то определитель n-го порядка записывают в виде](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-41.jpg)




![Определитель n-го порядка матрицы A = [aij] можно вычислять: 1) путем разложения по элементам i-й строки:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-46.jpg)












![Если A = [aij] то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/589503/slide-59.jpg)


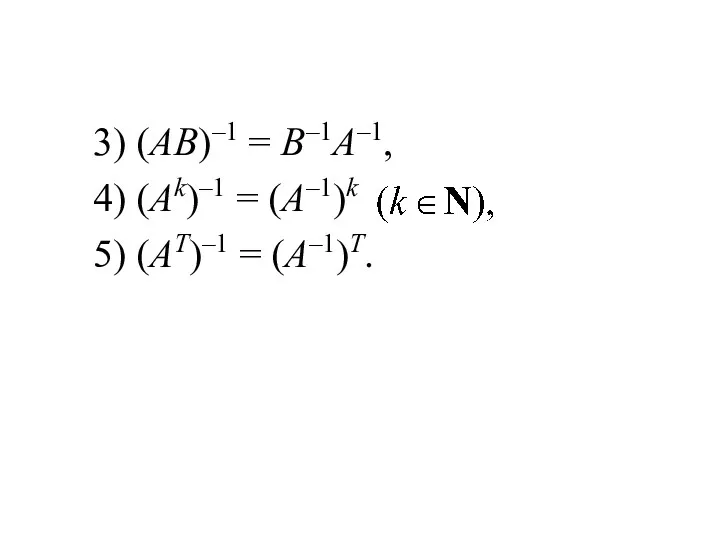








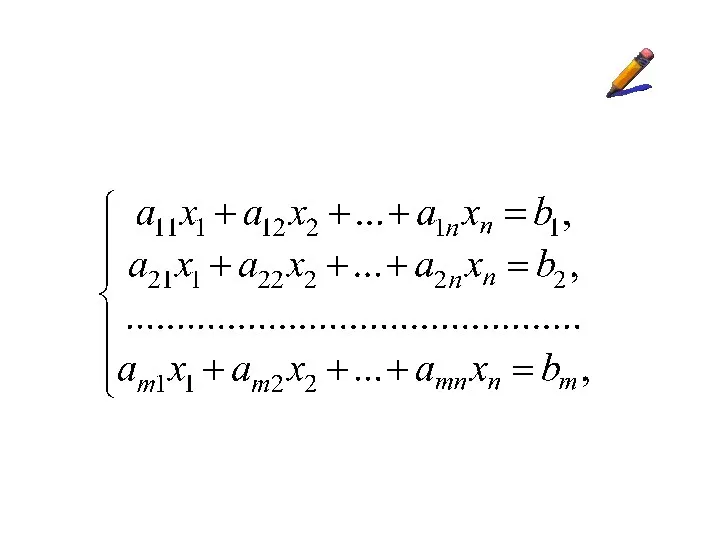




















 презентация к уроку математики 4 класс Решение задач(школа 2100)
презентация к уроку математики 4 класс Решение задач(школа 2100) Решение неполных квадратных уравнений
Решение неполных квадратных уравнений Математический турнир
Математический турнир Функции y = tgx и y = ctgx, их свойства и графики
Функции y = tgx и y = ctgx, их свойства и графики Организация непрерывной непосредственно образовательной деятельности детей в младшей группе по теме: Обобщение понятий много, один. Диск
Организация непрерывной непосредственно образовательной деятельности детей в младшей группе по теме: Обобщение понятий много, один. Диск Виды простых задач. 1 класс
Виды простых задач. 1 класс Числовые характеристики случайной величины. Лекция 2
Числовые характеристики случайной величины. Лекция 2 Площадь круга
Площадь круга Метод алгебраического сложения
Метод алгебраического сложения Понятие цилиндра
Понятие цилиндра Устный счёт
Устный счёт Использование конструкции для решения комбинаторных задач. Правило сложения
Использование конструкции для решения комбинаторных задач. Правило сложения Кестелімәліметтердің графикалық ұсынылуы
Кестелімәліметтердің графикалық ұсынылуы Геометрическая прогрессия. Формула п-го члена
Геометрическая прогрессия. Формула п-го члена Физико – математический турнир для учащихся 10-11 классов
Физико – математический турнир для учащихся 10-11 классов Относительная частота случайного события
Относительная частота случайного события Степень с целым показателем. 8 класс
Степень с целым показателем. 8 класс Презентация к уроку
Презентация к уроку Двугранный и многогранный угол_ Представление о правильных многогранниках
Двугранный и многогранный угол_ Представление о правильных многогранниках Решение задач по теории вероятности
Решение задач по теории вероятности Софья Ковалевская
Софья Ковалевская Множення десяткових дробів
Множення десяткових дробів Интерполяция, экстраполяция, аппроксимация
Интерполяция, экстраполяция, аппроксимация Турнир знатоков математики. 7-8 класс
Турнир знатоков математики. 7-8 класс Танграм
Танграм Деление окружности на равные части
Деление окружности на равные части Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений Параллельные прямые
Параллельные прямые