Содержание
- 2. Цель лекции Изучить понятие имитационного моделирования. Определить его цель, виды и области применения. Подробно рассмотреть метод
- 3. Содержание лекции Имитационное моделирование. Цель, виды и области применения имитационного моделирования. Статистическое моделирование. Метод Монте-Карло. Примеры
- 4. ЧТО ТАКОЕ ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ?
- 5. Имитация Имитация – это процесс «выполнения» модели, проводящий ее через (дискретные или непрерывные) изменения состояния во
- 6. Имитационное моделирование Имитационное моделирование – это: Метод, позволяющий строить модели, описывающие процессы так, как они проходили
- 7. Использование имитационного моделирования Дорого или невозможно экспериментировать на реальном объекте. Возникновение трудностей при построении математической модели
- 8. Преимущества имитационного моделирования Возможность решения более сложных задач. Просто учитывать такие факторы, как: наличие дискретных и
- 9. Применение имитационного моделирования Для оценки вариантов структуры системы. Для оценки вариантов эффективности различных алгоритмов управления системой.
- 10. Области применения имитационного моделирования Физические процессы. Материаловедение. Нанотехнологии. Бизнес процессы. Производство. Информационная безопасность и др.
- 11. Методы имитационного моделирования Метод статистических испытаний (Монте-Карло) – общее название группы численных методов, основанных на получении
- 12. МЕТОД МОНТЕ-КАРЛО
- 13. Метод Монте-Карло Название метода происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом. Одним
- 14. История метода Монте-Карло 1878 год. Возникновение идеи использования случайных явлений в области приближенных вычислений (работа Холла
- 15. Принципы получения случайных величин Рулетка. Простейшая схема – вращающийся диск с цифрами, резко останавливающийся для определения
- 16. Псевдослучайные числа Числа, получаемые по какой-либо формуле и имитирующие значения случайной величины, называются псевдослучайными. Первый метод
- 17. Сущность метода Монте-Карло Требуется найти значение «а» некоторой изучаемой величины. Для этого выбирают такую случайную величину
- 18. Преимущества и недостатки метода Преимущества: не требует никаких предложений о регулярности; приводит к выполнимой процедуре в
- 19. Применение метода Монте-Карло Первоначально метод использовался для решения задач нейтронной физики, где традиционные численные методы оказались
- 20. СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
- 21. Сущность метода В данном методе искомую величину представляют математическим ожиданием числовой функции от случайного исхода явления:
- 22. Преимущества и недостатки метода Преимущества: Универсальность. Не требует большого объема памяти. Недостатки: Большие случайные погрешности. Статическая
- 23. Роберт Гук Пьер Симон Лаплас Джеймс Клерк Максвелл Эрвин Шредингер Математические модели в физике Одна из
- 24. Математические модели в физике Уравнения баланса (законы сохранения). Массы. Импульса . Энергии. Уравнение диффузии. Уравнения движения
- 25. Математические модели в химии Первая попытка по применению математики в химии ‒ 1741 год М.В. Ломоносовым
- 26. этилен К.М. Гульдберг (слева) и П. Вааге. Якоб Хендрик Вант-Гофф Математические модели в химии Самая известная
- 27. Методы математической химии Теория графов (химическая кинетика). Топология (стереохимия и исследования свойств поверхностей потенциальной энергии). Теория
- 28. Томас Мальтус Леонардо Пизанский Математические модели в биологии Динамика популяций. Ряд Фибоначчи 1, 1, 2, 3,
- 29. Виды моделей в биологии Биологические. В нашем курсе мы их не рассматриваем. Физико-химические. С 60-х гг.
- 30. Модель «хищник-жертва» Численности популяций жертв и хищников зависят только от времени. В отсутствие взаимодействия численность видов
- 31. Рональд Эйлмер Фишер Мотоо Кимура Модели эволюции Синтетическая теория эволюции (с начала 20в.). Исследования Drosophila ‒
- 32. Применение моделей в биологии Изучение биологических структур, функций и процессов на разных уровнях организации живого: Молекулярном.
- 33. Заключение и выводы Изучены цель, виды и области применения имитационного моделирования. Подробно рассмотрены метод статистического моделирования
- 35. Скачать презентацию
































 Цифры Диск
Цифры Диск конспект урока по математике во 2 классе. УМК Перспективная начальная школа. Тема урока Периметр многоугольника.
конспект урока по математике во 2 классе. УМК Перспективная начальная школа. Тема урока Периметр многоугольника. Математическое моделирование в приборных системах. Построение математической модели и вычислительный эксперимент. (Лекция 2)
Математическое моделирование в приборных системах. Построение математической модели и вычислительный эксперимент. (Лекция 2) Презентации для занятий. Тема: Основы геометрии. Геометрические фигуры.
Презентации для занятий. Тема: Основы геометрии. Геометрические фигуры. Угол между скрещивающимися прямыми
Угол между скрещивающимися прямыми 12 апреля - День космонавтики. Урок математики
12 апреля - День космонавтики. Урок математики Числа вида: 1, 2, 3, 4, 5
Числа вида: 1, 2, 3, 4, 5 Треугольник. Виды треугольников
Треугольник. Виды треугольников Расчет каналов. Гидравлика
Расчет каналов. Гидравлика Круговая диаграмма
Круговая диаграмма Второй и третий признаки равенства треугольников. 7 класс
Второй и третий признаки равенства треугольников. 7 класс В стране математики.
В стране математики. Эксперимент по методу Монте-Карло. Истинная модель. Соответствующая модель
Эксперимент по методу Монте-Карло. Истинная модель. Соответствующая модель Задачи на кратное сравнение
Задачи на кратное сравнение Пирамида
Пирамида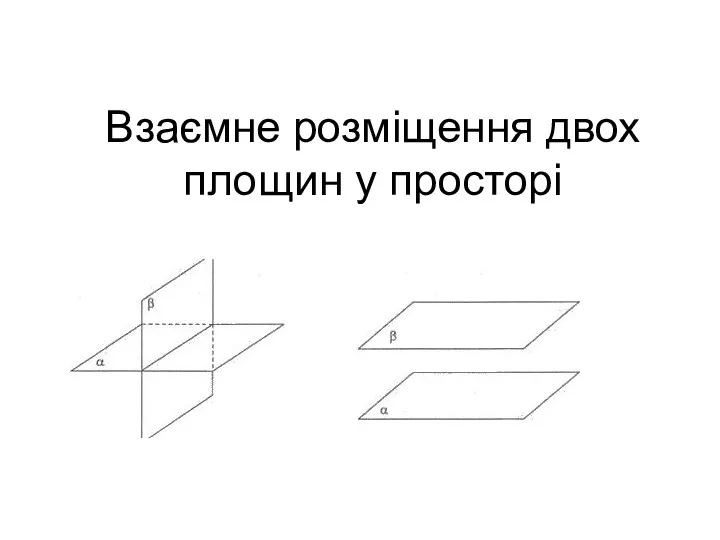 Взаємне розміщення двох площин у просторі
Взаємне розміщення двох площин у просторі Внеклассное мероприятие по математике
Внеклассное мероприятие по математике Новое свойство квадратных уравнений
Новое свойство квадратных уравнений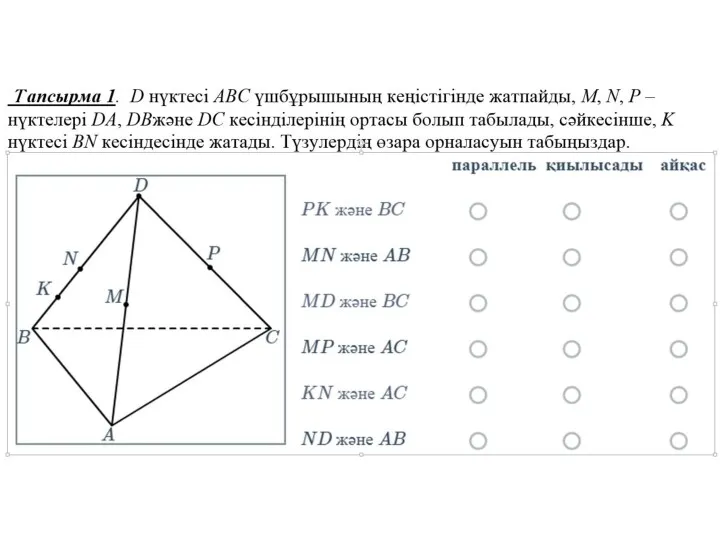 Суретте тікбұрышты параллелепипед бейнеленген
Суретте тікбұрышты параллелепипед бейнеленген Письменное деление на двузначное число
Письменное деление на двузначное число Презентация Использование дидактических игр с перфокартами в работе с детьми старшего дошкольного возраста по ФЭМП
Презентация Использование дидактических игр с перфокартами в работе с детьми старшего дошкольного возраста по ФЭМП Решение неравенств с одной переменной
Решение неравенств с одной переменной Сумма углов выпуклого многоугольника
Сумма углов выпуклого многоугольника Использование графиков функций при решении неравенств. Задания для устного счета
Использование графиков функций при решении неравенств. Задания для устного счета Тройной интеграл
Тройной интеграл Ряд натуральных чисел
Ряд натуральных чисел Выражение с переменной
Выражение с переменной Свойства прямоугольных треугольников. Задачи
Свойства прямоугольных треугольников. Задачи