Содержание
- 2. Лекция 1 2. Экстремум функции. Необходимое условие существования экстремума. 3. Первый достаточный признак экстремума. 4. Общая
- 3. 6. Точки перегиба. 8. Общая схема построения графика. 5. Исследование на экстремум с помощью производных высших
- 4. Для того чтобы дифференцируемая на (а,в) функция f(x) не убывала (не возрастала), необходимо и достаточно, чтобы
- 5. Локальные максимумы и минимумы функции называется её экстремумами.
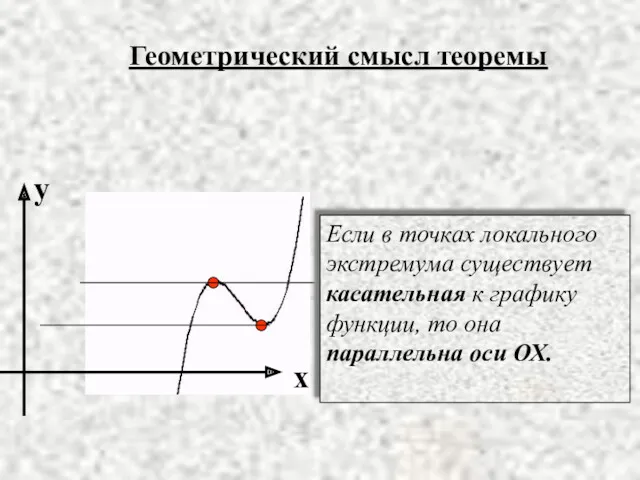
- 7. Геометрический смысл теоремы Если в точках локального экстремума существует касательная к графику функции, то она параллельна
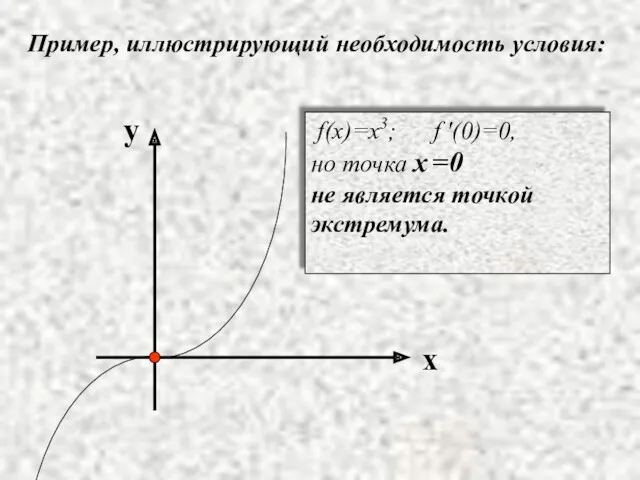
- 8. Пример, иллюстрирующий необходимость условия: f(x)=x3; f '(0)=0, но точка x =0 не является точкой экстремума.
- 9. Следствия. Если f(x) дифференцируема на (a,b), то она может иметь экстремумы только в тех точках, где
- 10. Точка x0 является точкой экстремума f(x), если её производная f '(x) меняет знак при переходе через
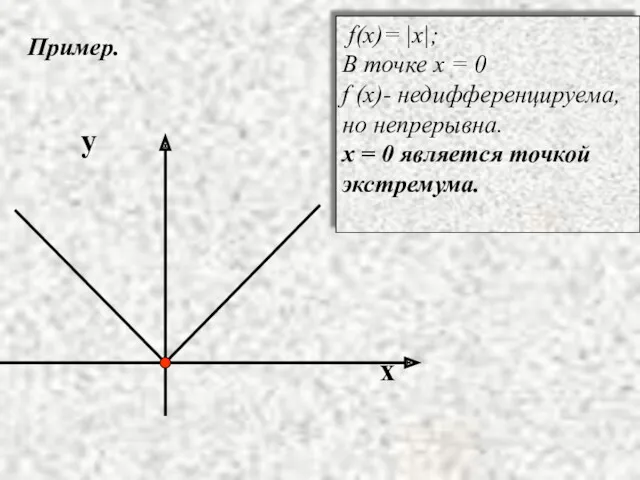
- 11. Пример. x y f(x)= |x|; В точке x = 0 f (x)- недифференцируема, но непрерывна. x
- 12. Пусть f(x) непрерывна на (a,b) и дифференцируема всюду за исключением конечного числа точек (a,b) . 1.Находим
- 13. 4. По характеру смены знака f '(x) при переходе через критические точки определяем вид экстремума (max
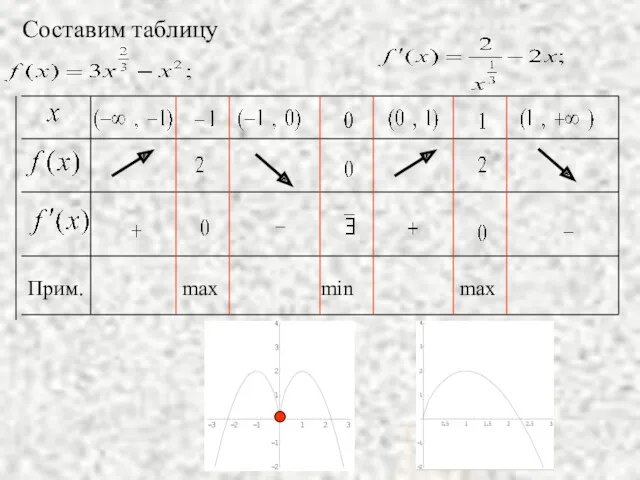
- 14. Прим. max min max Составим таблицу
- 15. Тогда: с - точка локального минимума 1) если f ''(c) > 0, то 2) если f
- 16. Доказательство:
- 17. Пусть f(x) имеет в критической точке x=c отличную от нуля производную чётного порядка f (2n) (c)
- 18. Пример. a - точка локального минимума.
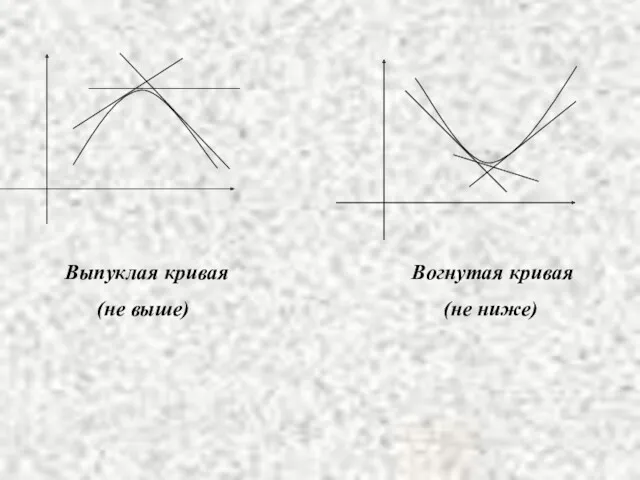
- 20. Выпуклая кривая (не выше) Вогнутая кривая (не ниже)
- 21. Если во всех точках (a,b) f ''(x) Пример. График f (x) - выпуклая линия Если во
- 23. Если точка x0 является точкой перегиба графика функции y=f(x) , то либо f ''(x0) = 0
- 24. Если f ''(x0) = 0 , то x0 не обязательно будет точкой перегиба. (Пример : y
- 25. Если f ''(x) меняет знак при переходе через точку x0, то эта точка является точкой перегиба.
- 27. Замечание. Пример.
- 29. необходимо и достаточно существование пределов:
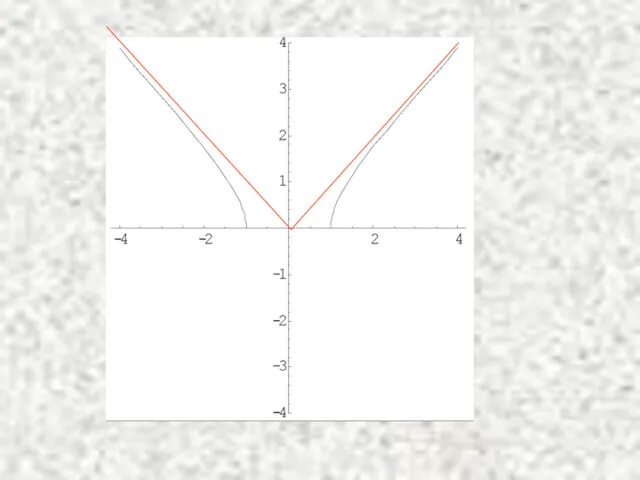
- 30. Замечание. Точно так же определяется наклонная асимптота и формулируется критерий её существования для случая Пример. Найти
- 31. 2)
- 33. Исследование функции f(x) состоит из трёх этапов. 1. Область определения. I. Информация из вида f(x). 2.
- 34. 3. Асимптоты. 4. Точки пересечения с осями координат. II. Информация из вида f '(x). ( Исследование
- 35. V. Построение Графика. Вначале проводятся асимптоты, ставятся опорные точки, найденные на этапах I-III, строится линия графика.
- 36. 2. Функция общего вида.
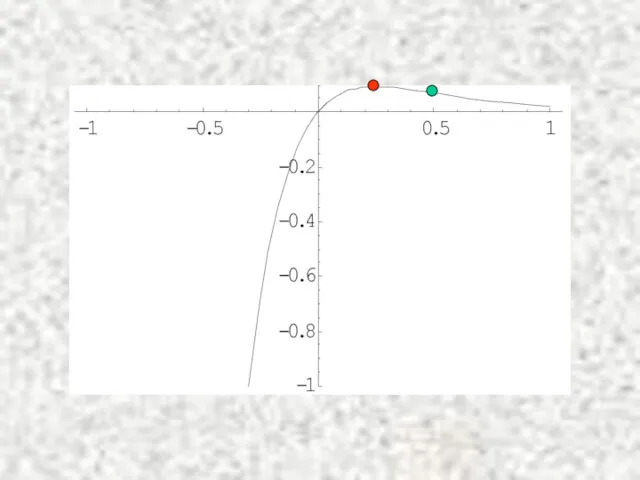
- 37. Прим. max перегиб
- 41. Скачать презентацию

















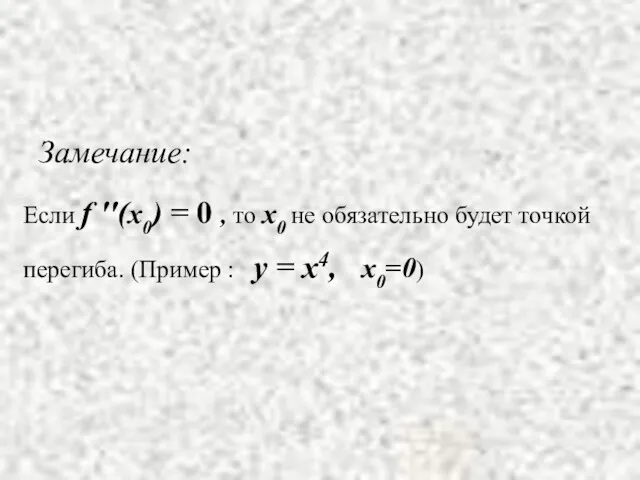













 Повторение. 8 класс
Повторение. 8 класс закрепление изученного материала
закрепление изученного материала Проверка значимости в парной линейной регрессии
Проверка значимости в парной линейной регрессии Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Теорема Пифагора. Египетский треугольник
Теорема Пифагора. Египетский треугольник Математика в мире животных. 5 класс
Математика в мире животных. 5 класс Презентация к открытому уроку по математике
Презентация к открытому уроку по математике Класифікація кутів
Класифікація кутів Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Тренажер по математике для 1 класса. Сложение и вычитание в пределах 10
Тренажер по математике для 1 класса. Сложение и вычитание в пределах 10 Изучаем геометрические фигуры
Изучаем геометрические фигуры Внеклассное мероприятие по математике Звездный час
Внеклассное мероприятие по математике Звездный час Параллель, қиылысатын және айқас түзулер
Параллель, қиылысатын және айқас түзулер Урок-сказка по теме Натуральные числа по мотивам сказки Золотой ключик
Урок-сказка по теме Натуральные числа по мотивам сказки Золотой ключик Урок математики Во 2 классе Тема: Урок повторения изученного с элементами материалов окружающего мира
Урок математики Во 2 классе Тема: Урок повторения изученного с элементами материалов окружающего мира Вероятность и статистика. 7 класс
Вероятность и статистика. 7 класс Монотонные последовательности. Теорема Вейерштрасса
Монотонные последовательности. Теорема Вейерштрасса Математическая игра Счастливый случай. 5 класс
Математическая игра Счастливый случай. 5 класс Урок – игра В царстве квадратных корней
Урок – игра В царстве квадратных корней Презентация к уроку математики в 1 классе Решение задач и примеров в пределах 10
Презентация к уроку математики в 1 классе Решение задач и примеров в пределах 10 Умножение и деление десятичных дробей. Урок-путешествие
Умножение и деление десятичных дробей. Урок-путешествие Ֆունկցիայի գրաֆիկի ձևափոխություններ
Ֆունկցիայի գրաֆիկի ձևափոխություններ II признак равенства треугольников
II признак равенства треугольников Биостатистика. Критерии согласия Колмогорова-Смирнова
Биостатистика. Критерии согласия Колмогорова-Смирнова Периметр прямокутника
Периметр прямокутника Параллельные прямые
Параллельные прямые Приключение принцессы Софии
Приключение принцессы Софии Геометрические характеристики плоских сечений
Геометрические характеристики плоских сечений