Содержание
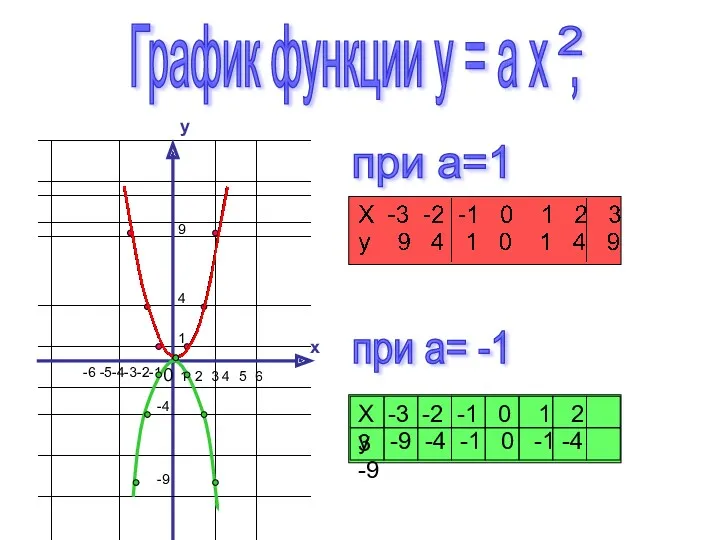
- 2. y x 0 График функции y = a x , 2 при a=1 при a= -1
- 3. Преобразование графика квадратичной функции
- 4. Построение графиков функций у=х2 и у=х2+m.
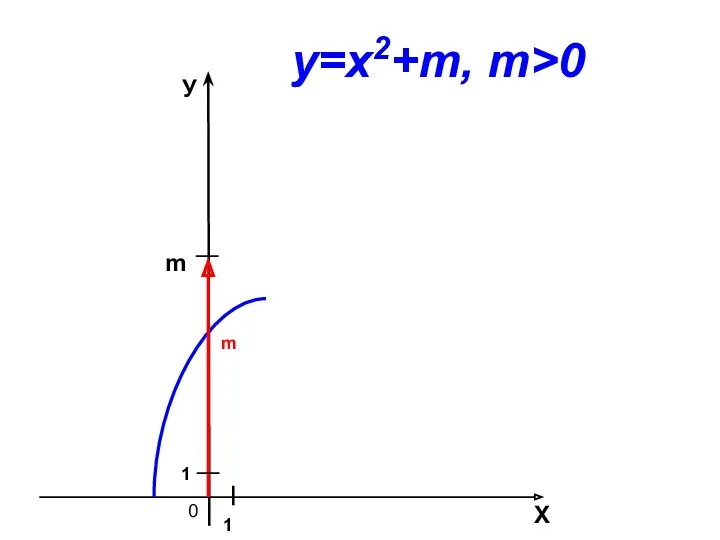
- 5. 0 m Х У 1 1 у=х2+m, m>0
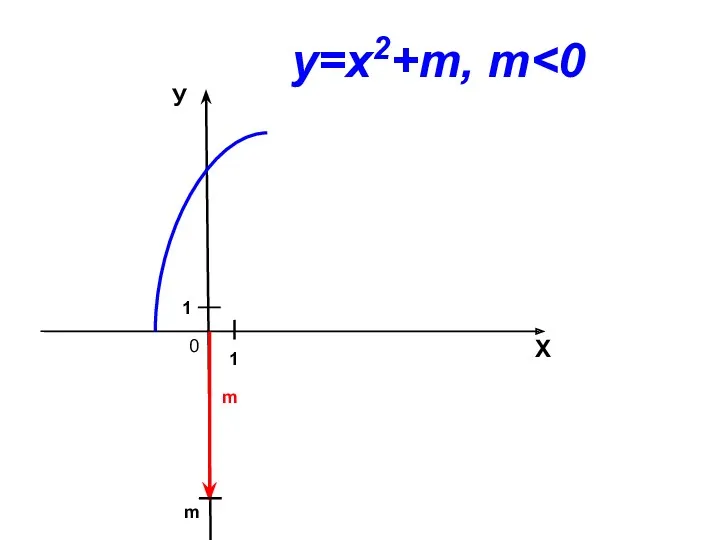
- 6. 0 Х У 1 1 m у=х2+m, m
- 7. Постройте в одной координатной плоскости графики функций:
- 8. Построение графиков функций у=х2 и у=(х+l)2.
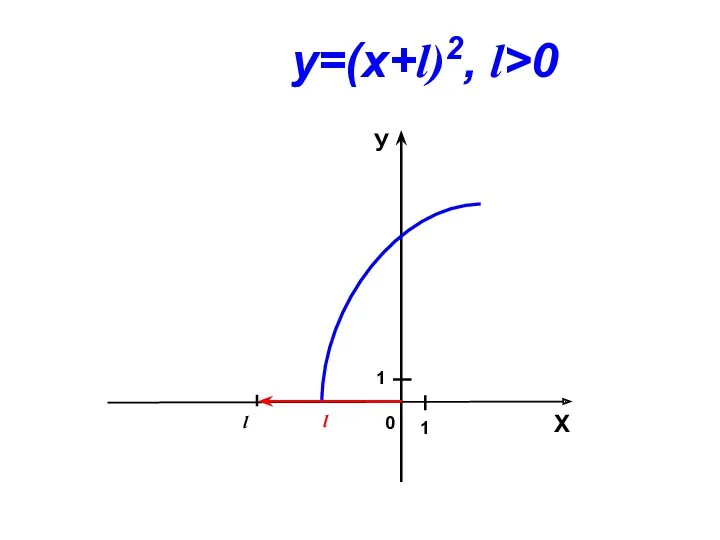
- 9. 0 l Х У 1 1 у=(х+l)2, l>0
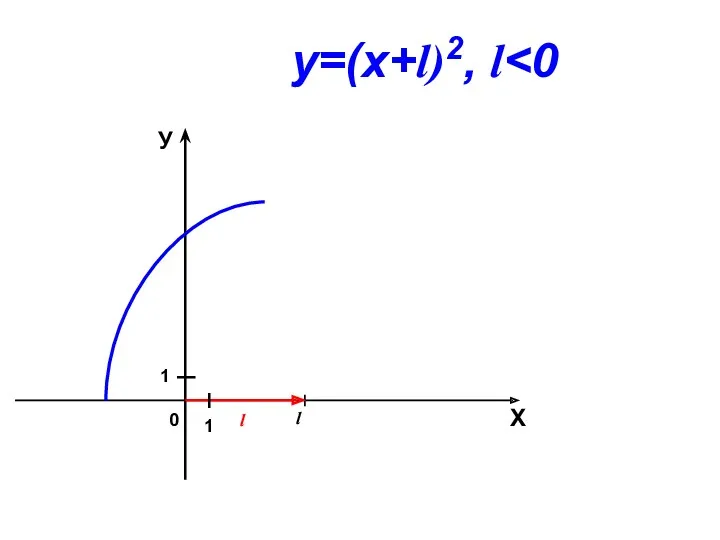
- 10. 0 l Х У 1 1 у=(х+l)2, l
- 11. Постройте в одной координатной плоскости графики функций:
- 12. Найти координаты вершины параболы: У=2(х-4)² +5 У=-6(х-1)² У = -х²+12 У= х²+4 У= (х+7)² - 9
- 13. График квадратичной функции, его свойства
- 14. Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c, где х - независимая переменная, a,
- 15. Графиком квадратичной функции является парабола, ветви которой направлены вверх(если а>0) или вниз (если а у=2х²+4х-1 –
- 16. Определить координату вершины параболы по формулам: Отметить эту точку на координатной плоскости. Через вершину параболы начертить
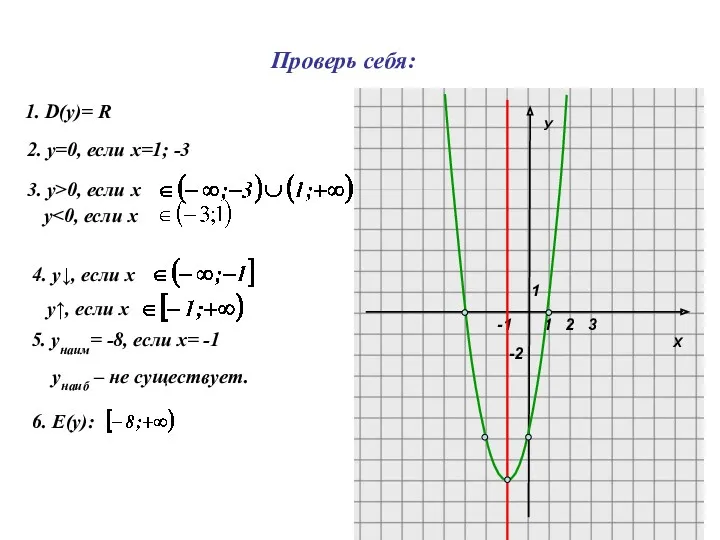
- 17. Постройте график функции у=2х²+4х-6, опишите его свойства
- 18. Х У 1 1 -2 2 3 -1 1. D(y)= R 2. у=0, если х=1; -3
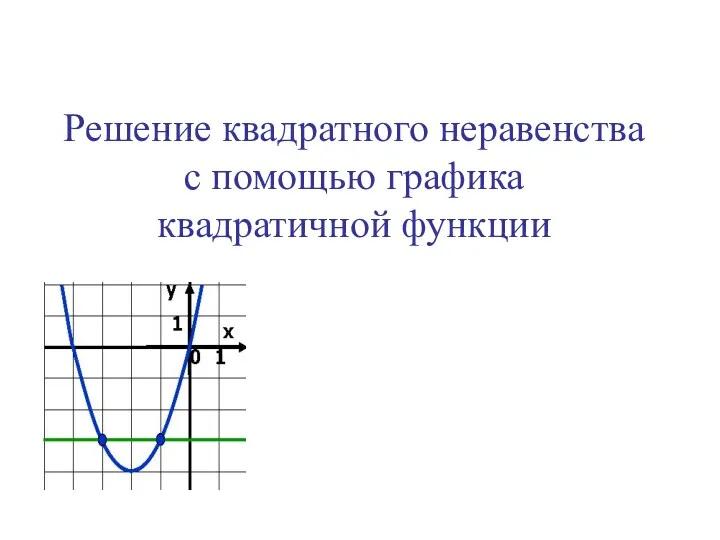
- 19. Решение квадратного неравенства с помощью графика квадратичной функции
- 20. Определение: Неравенство, левая часть которого есть многочлен второй степени, а правая- нуль, называется неравенством второй степени.
- 21. Какие из неравенств вы бы назвали неравенствами второй степени: 1) 6х 2-13х>0; 2) x 2-3x-14>0; 3)
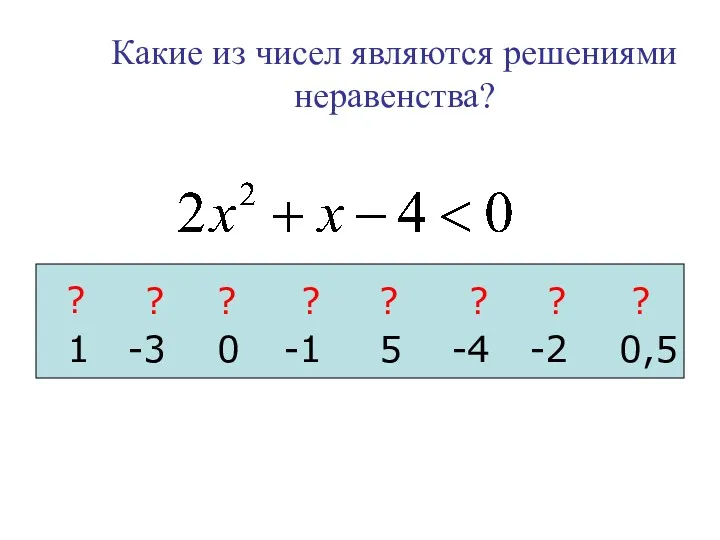
- 22. Какие из чисел являются решениями неравенства? 1 -3 0 -1 5 -4 -2 0,5 ? ?
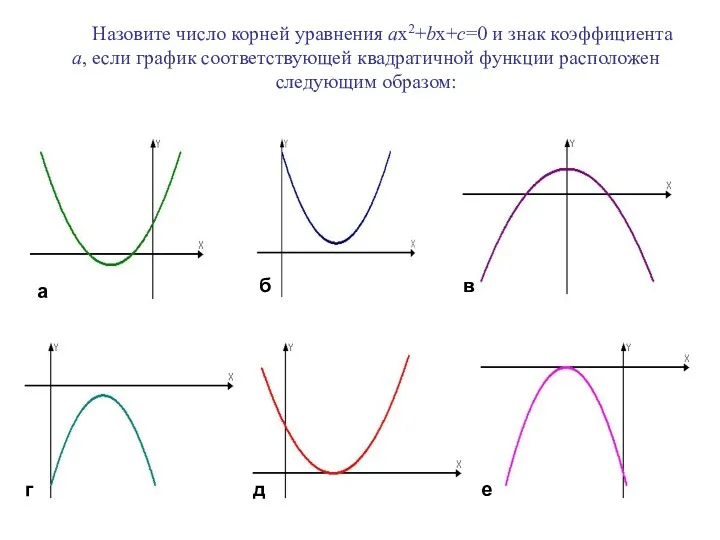
- 23. Назовите число корней уравнения ax2+bx+c=0 и знак коэффициента а, если график соответствующей квадратичной функции расположен следующим
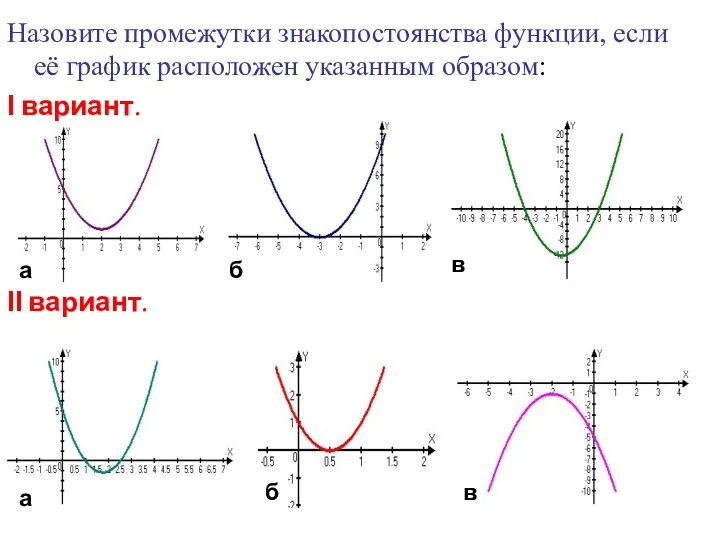
- 24. Назовите промежутки знакопостоянства функции, если её график расположен указанным образом: Ι вариант. ΙІ вариант. в б
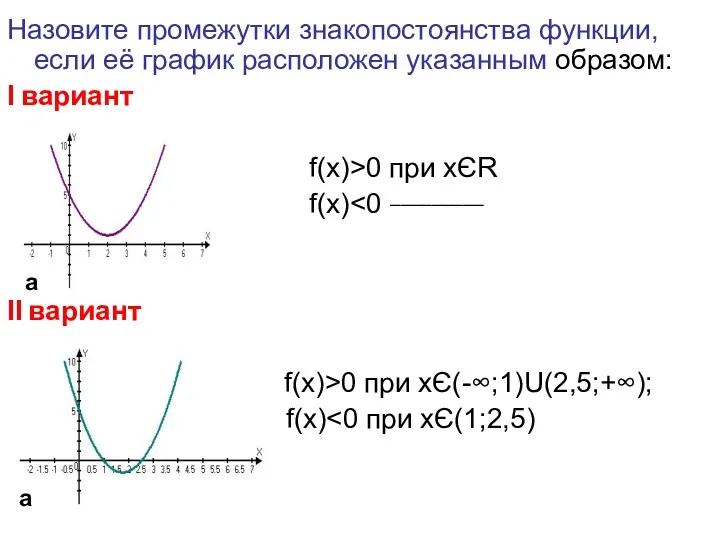
- 25. Назовите промежутки знакопостоянства функции, если её график расположен указанным образом: Ι вариант f(x)>0 при xЄR f(x)
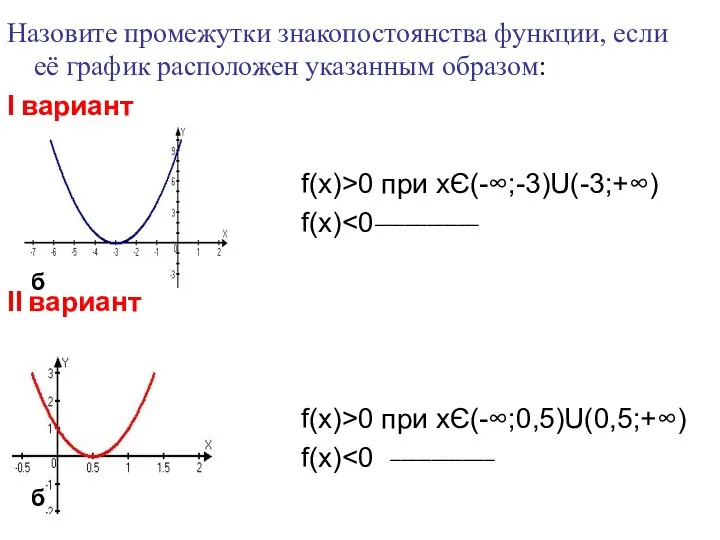
- 26. Назовите промежутки знакопостоянства функции, если её график расположен указанным образом: Ι вариант f(x)>0 при xЄ(-∞;-3)U(-3;+∞) f(x)
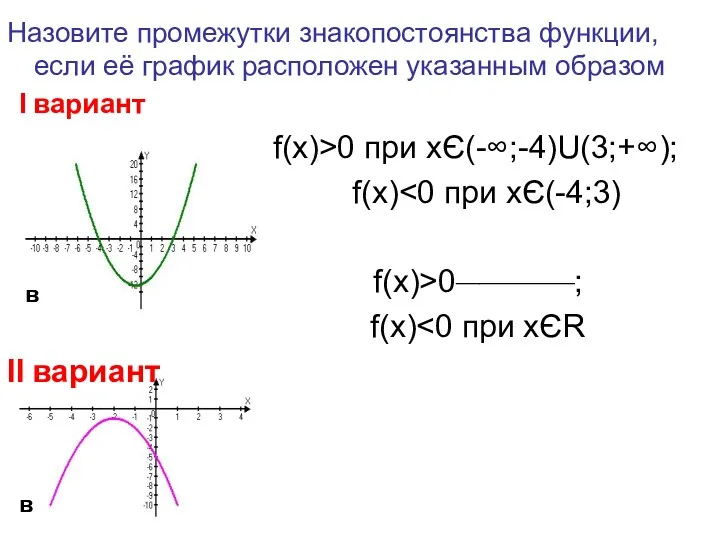
- 27. Назовите промежутки знакопостоянства функции, если её график расположен указанным образом Ι вариант f(x)>0 при xЄ(-∞;-4)U(3;+∞); f(x)
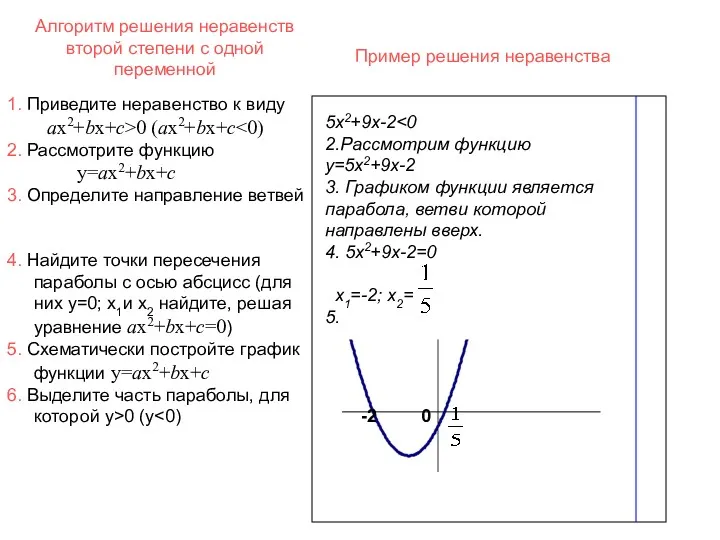
- 28. Алгоритм решения неравенств второй степени с одной переменной 5х2+9х-2 2.Рассмотрим функцию y=5х2+9х-2 3. Графиком функции является
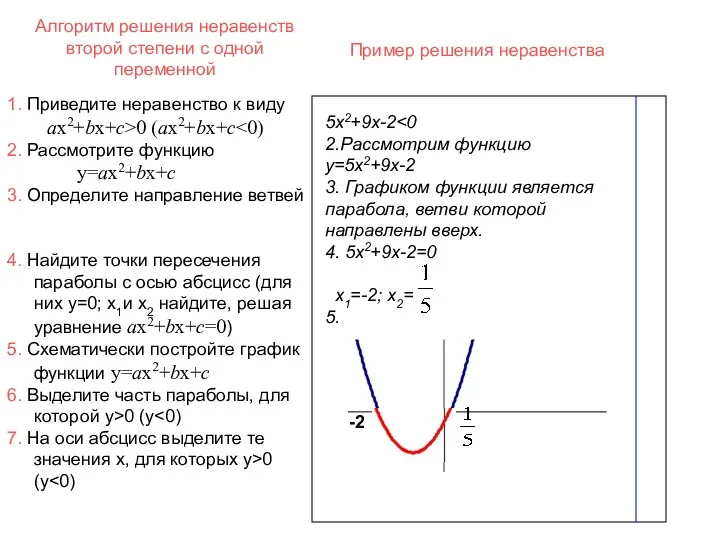
- 29. Алгоритм решения неравенств второй степени с одной переменной 5х2+9х-2 2.Рассмотрим функцию y=5х2+9х-2 3. Графиком функции является
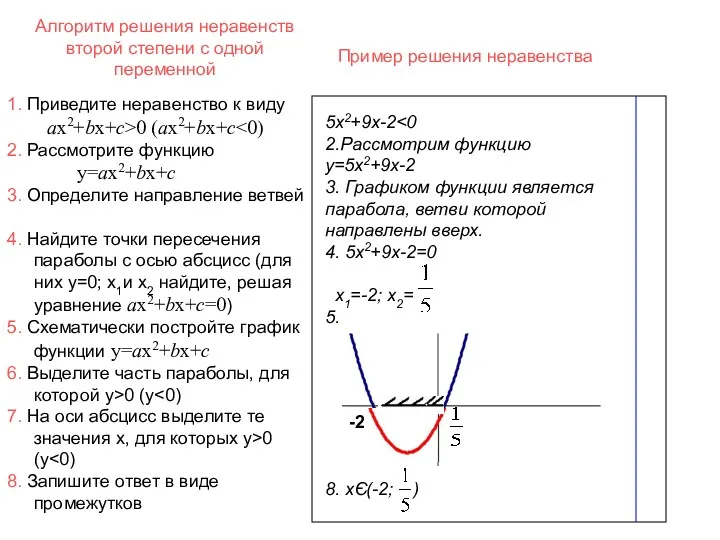
- 30. Алгоритм решения неравенств второй степени с одной переменной 5х2+9х-2 2.Рассмотрим функцию y=5х2+9х-2 3. Графиком функции является
- 31. В таблице 1 найдите верное решение неравенства 1, в таблице 2 - решение неравенства 2: 1.
- 32. В таблице 1 найдите верное решение неравенства 1, в таблице 2- решение неравенства 2: 1. 2.
- 33. В таблице 1 найдите верное решение неравенства 1, в таблице 2- решение неравенства 2: 1. 2.
- 34. В таблице 1 найдите верное решение неравенства 1, в таблице 2- решение неравенства 2: 1. 2.
- 35. Итог урока При решении данных заданий нам удалось систематизировать знания о применении квадратичной функции. Математика- это
- 36. Незаконченное предложение Задание: закончить одно из трех предложений, которое больше других соответствует вашему состоянию. “Выполнять задания
- 37. Домашнее задание Учебник №142; №190
- 39. Скачать презентацию




















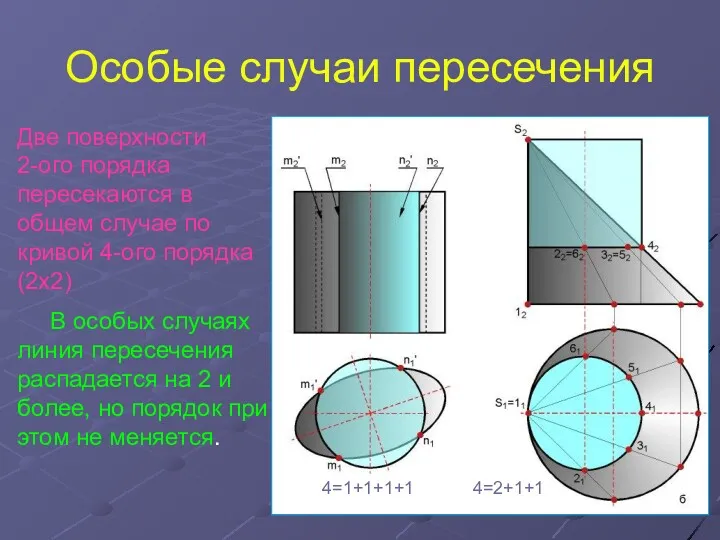 Особые случаи пересечения. Пересечение соосных поверхностей вращения. Теорема Монжа
Особые случаи пересечения. Пересечение соосных поверхностей вращения. Теорема Монжа Урок Сложение двузначных чисел в столбик, технология проблемного обучения
Урок Сложение двузначных чисел в столбик, технология проблемного обучения Математический калейдоскоп
Математический калейдоскоп Властивості тригонометричних функцій. Алгебра. 10 клас
Властивості тригонометричних функцій. Алгебра. 10 клас Геометрические тела
Геометрические тела Раздел математики - геометрия
Раздел математики - геометрия Внеклассное занятие (КВН) по математике 1 класс Диск
Внеклассное занятие (КВН) по математике 1 класс Диск Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника
Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника Задачи на повторение по геометрии. Подготовка к ГИА
Задачи на повторение по геометрии. Подготовка к ГИА Формула Пика
Формула Пика Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Понятие дроби. Основные свойства дроби
Понятие дроби. Основные свойства дроби Многоугольники. Ломаная
Многоугольники. Ломаная Деление отрезка на 2,4,8 равных частей
Деление отрезка на 2,4,8 равных частей Скорость. Время. Расстояние
Скорость. Время. Расстояние Одночлен
Одночлен Тема: Арифметические действия над числами (урок 1.27)
Тема: Арифметические действия над числами (урок 1.27) Начертательная геометрия. Пересечение прямой линии с поверхностью. (Лекция 6)
Начертательная геометрия. Пересечение прямой линии с поверхностью. (Лекция 6) Формирование навыков смыслового чтения на уроках математики и во внеурочной деятельности
Формирование навыков смыслового чтения на уроках математики и во внеурочной деятельности Приёмы табличного вычитания однозначных чисел с переходом через десяток
Приёмы табличного вычитания однозначных чисел с переходом через десяток Линейная функция и её график
Линейная функция и её график Понятие вероятности. Случайные исходы, события, испытания
Понятие вероятности. Случайные исходы, события, испытания Приёмы умножения числа 2. Деление на 2
Приёмы умножения числа 2. Деление на 2 Теоретический материал для решения задач на движение
Теоретический материал для решения задач на движение Элементы корреляционного и регрессионного анализа
Элементы корреляционного и регрессионного анализа Учим таблицу умножения
Учим таблицу умножения Кластерный анализ
Кластерный анализ Triangle. Inequalities
Triangle. Inequalities