Содержание
- 2. Автор: Лотфи А. Заде. Американский математик и логик, автор термина нечёткая логика и один из основателей
- 3. Теория нечетких моделей
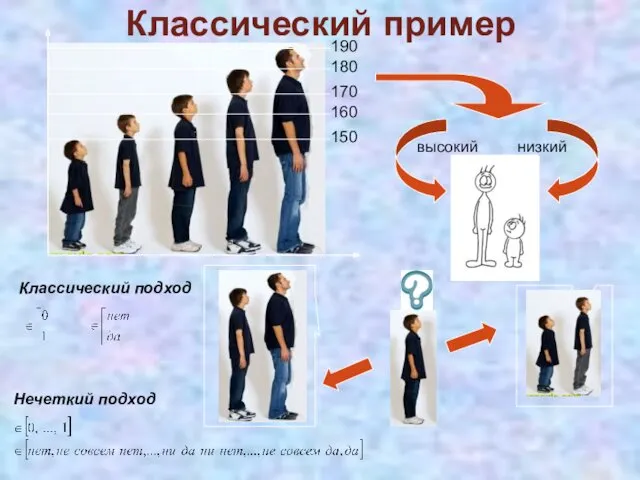
- 4. 150 160 170 180 190 высокий низкий Классический подход Нечеткий подход Классический пример
- 5. Применение нечетких моделей при принятии решений и в процессе моделирования целесообразно в случаях, когда имеется недостаточность
- 6. Достоинством применения нечетких моделей является бОльшая прозрачность (по сравнению с искусственными нейронными сетями) за счет возможности
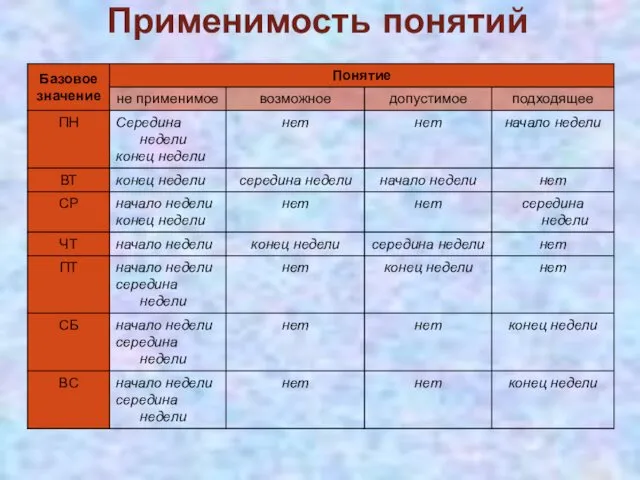
- 8. Базовые и нечеткие значения переменных
- 9. При этом различные элементы из множества нечетких значений в различной степени могут быть применимы к конкретному
- 10. Применимость понятий
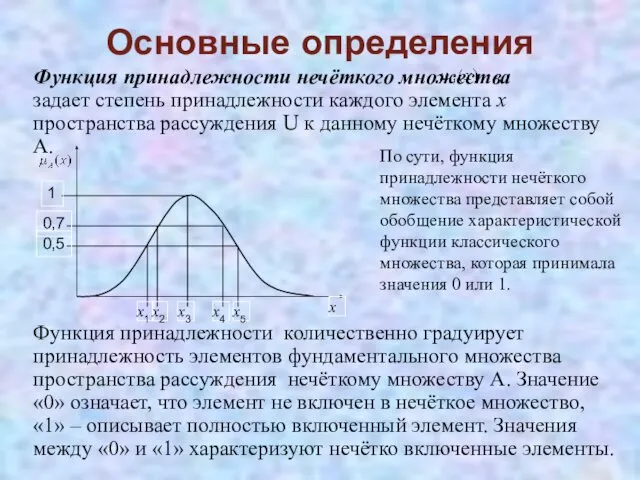
- 11. Основные определения Функция принадлежности нечёткого множества задает степень принадлежности каждого элемента х пространства рассуждения U к
- 12. Нечеткое множество А – совокупность пар , где U – область рассуждений, – функция принадлежности. Носитель
- 13. Высота h(A) нечеткого множества А – величина супремума для значений функции принадлежности множества А области рассуждений
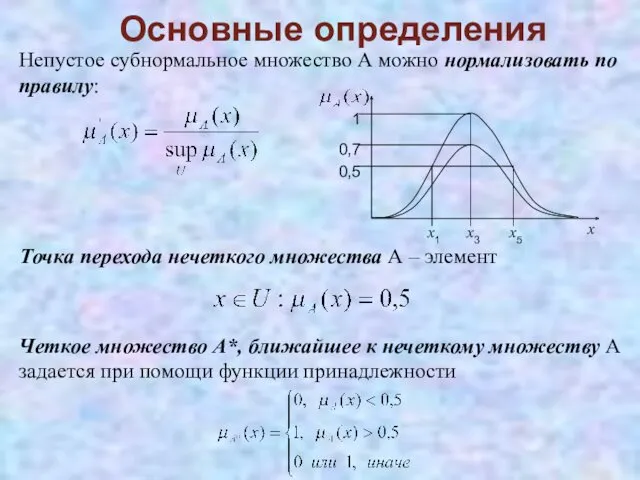
- 14. Непустое субнормальное множество А можно нормализовать по правилу: Точка перехода нечеткого множества А – элемент Четкое
- 15. Нечеткое множество А называется одноточечным, если его носитель состоит из единственной точки, обозначается Нечеткое множество А,
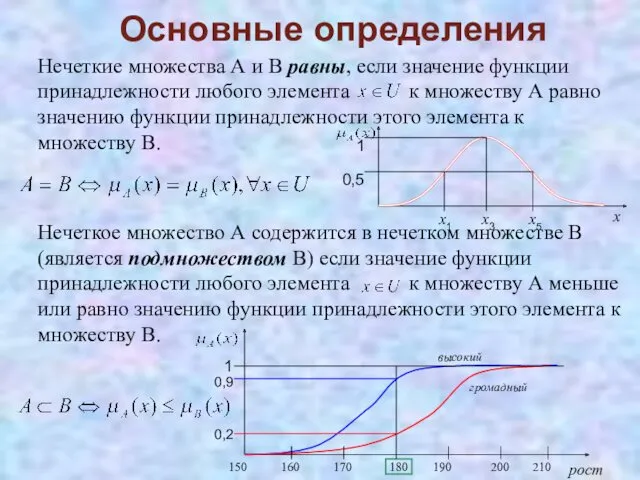
- 16. Нечеткие множества А и В равны, если значение функции принадлежности любого элемента к множеству А равно
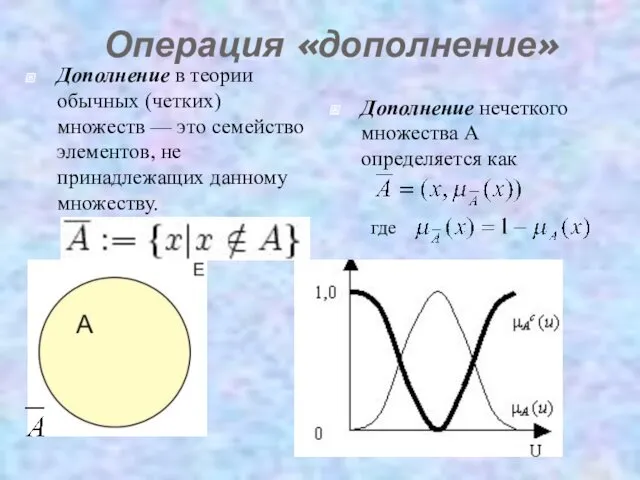
- 17. Операция «дополнение» Дополнение в теории обычных (четких) множеств — это семейство элементов, не принадлежащих данному множеству.
- 18. Операция «пересечение» Пересечение множеств в теории четких множеств — это множество, состоящее из элементов, которые принадлежат
- 19. Операция «объединение» Объединение множеств в теории четких множеств — это множество, содержащее в себе все элементы
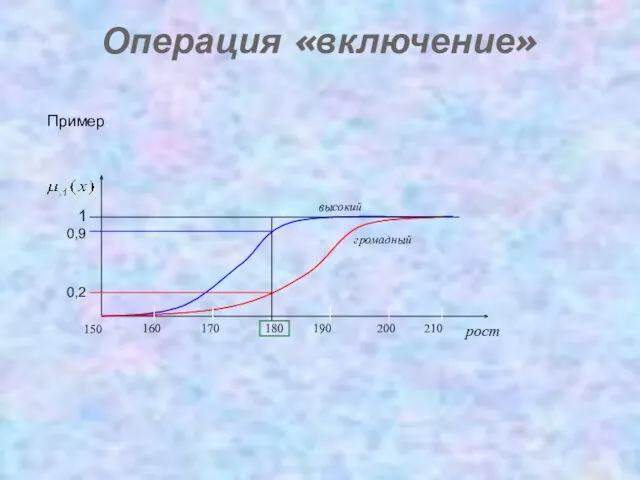
- 20. Операция «включение» В теории четких множеств, множество A содержится во множестве B (множество B включает множество
- 21. Операция «включение» Пример:
- 22. Операция «равенство» В теории четких множеств, два множества называются равными, если они являются подмножествами друг друга:
- 23. Степень включения и степень равенства Степенью включения нечеткого множества А в нечеткое множество В называется величина
- 24. Операции «концентрирование» и «растяжение» Операция концентрации В общем случае: Результатом применения операции концентрирования к нечеткому множеству
- 25. Операции «концентрирование» и «растяжение» Операция растяжения В общем случае: В частном случае: Операция растяжения повышает степень
- 26. Примеры отрицаний
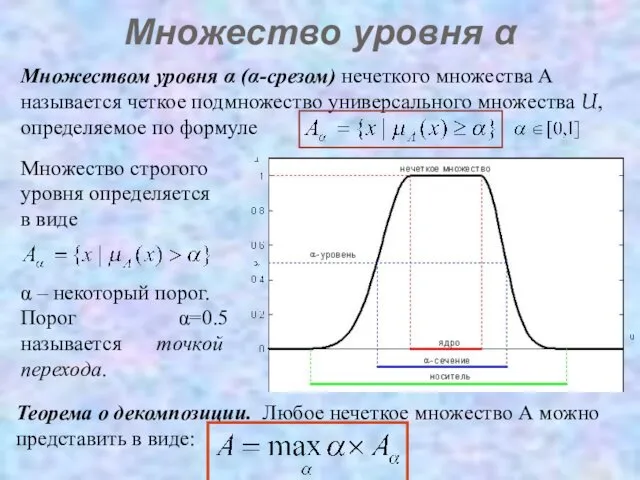
- 27. Множество уровня α Множеством уровня α (α-срезом) нечеткого множества А называется четкое подмножество универсального множества U,
- 29. Обычные (четкие) бинарные отношения Бинарным отношением R на множестве U называется некоторое подмножество декартова произведения .
- 30. Обычные (четкие) бинарные отношения Если множество U, на котором задано отношение R, конечно, то отношение задается
- 31. Примеры в виде матрицы Пусть дано множество U=(х1, х2, х3, х4), где х1 – собака х2
- 32. Нечетким бинарным отношением R на универсальном множестве называется нечеткое подмножество декартова произведения , которое характеризуется такой
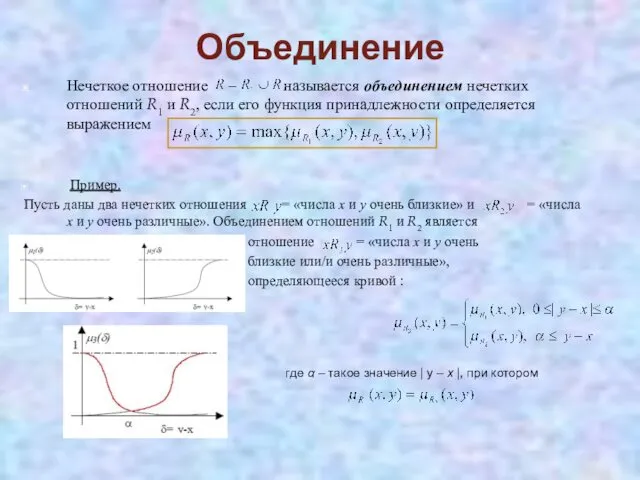
- 33. Объединение Нечеткое отношение называется объединением нечетких отношений R1 и R2, если его функция принадлежности определяется выражением
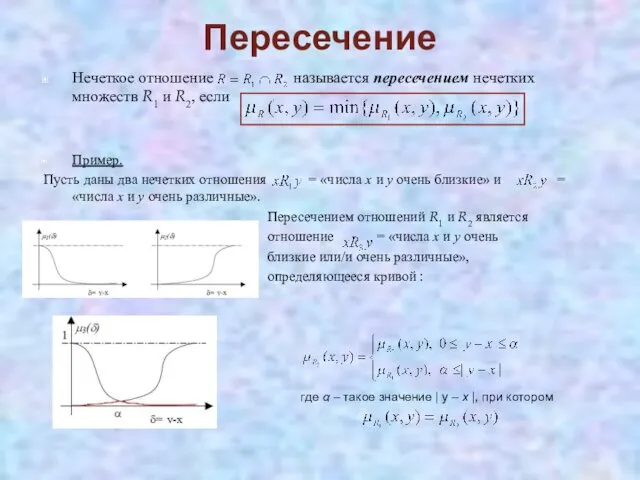
- 34. Пересечение Нечеткое отношение называется пересечением нечетких множеств R1 и R2, если Пример. Пусть даны два нечетких
- 36. Лингвистическая переменная Лингвистическая переменная – переменная, значением которой являются слова или предложения естественного или искусственного языка.
- 37. Лингвистическая переменная Лингвистическая переменная описывается набором где х – название переменной Т(х) – совокупность ее лингвистических
- 38. Лингвистическая переменная Конкретное название , порожденное синтаксическим правилом G, называется термом. Терм, который состоит из одного
- 39. Пример Рассмотрим лингвистическую переменную с именем х =«температура в комнате». Тогда оставшуюся четверку , можно определить
- 40. Лингвистическая переменная истинности В каждодневных разговорах мы часто характеризуем степень истинности утверждения посредством таких выражений, как
- 41. Под приближенными рассуждениями понимается процесс, при котором из нечетких посылок получают некоторые следствия, возможно, тоже нечеткие.
- 42. Правило modus ponens Пусть А и В — нечеткие высказывания и — соответствующие им функции принадлежности.
- 43. Различные импликации
- 44. Нечеткая база знаний Логико-лингвистические методы описания систем основаны на том, что поведение исследуемой системы описывается в
- 45. Нечеткий логический вывод Нечетким логическим выводом (fuzzy logic inference) называется аппроксимация зависимости Y=f(X1,X2,…,Xn) каждой выходной лингвистической
- 47. Основные определения Нечеткое число — это нечеткое подмножество универсального множества действительных чисел, имеющее нормальную и выпуклую
- 48. Основные определения Нечеткое число А унимодально, если условие справедливо только для одной точки действительной оси. Выпуклое
- 49. Нечеткие числа (L-R)-типа Нечеткие числа (L-R)-типа — это разновидность нечетких чисел специального вида, задаваемых по определенным
- 50. Пусть L и R– функции (L-R)-типа. Унимодальное нечеткое число А с модой а (т.е. ) задается
- 51. Треугольные числа Треугольным нечетким числом А называется тройка (a≤b≤c) действительных чисел, через которые его функция принадлежности
- 53. Скачать презентацию








































 Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Метрологическое обеспечение производства
Метрологическое обеспечение производства Число 3
Число 3 Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Большая математическая мастерская
Большая математическая мастерская Площадь прямоугольника. Единицы измерения площади
Площадь прямоугольника. Единицы измерения площади Чтение графиков. Тренажер
Чтение графиков. Тренажер Нелинейная регрессия
Нелинейная регрессия Законы арифметических действий
Законы арифметических действий Умножение числа 6 и деление на 6.
Умножение числа 6 и деление на 6. Урок математики во 2 классе
Урок математики во 2 классе Координатная плоскость. 6 класс
Координатная плоскость. 6 класс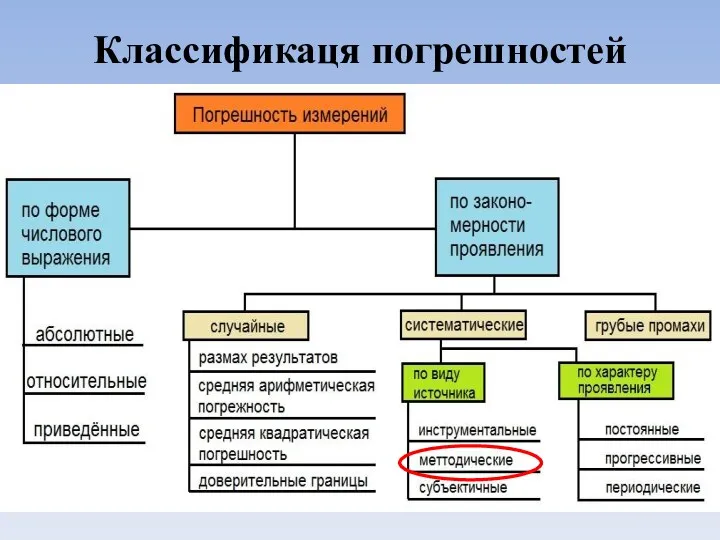 Классификаця погрешностей
Классификаця погрешностей Квадрат и куб (1 класс)
Квадрат и куб (1 класс) Числовой луч
Числовой луч Mathematics for еconomists. (Week 1-12)
Mathematics for еconomists. (Week 1-12) Квадрат түбірі бар өрнектерді түрлендіру
Квадрат түбірі бар өрнектерді түрлендіру Считай дальше
Считай дальше Урок математики в 1 классе по теме Равенство. Неравенство. УМК Школа России.
Урок математики в 1 классе по теме Равенство. Неравенство. УМК Школа России. Дроби. Устный счет
Дроби. Устный счет Конспект НОД Познание (ФЭМП) в старшей группе
Конспект НОД Познание (ФЭМП) в старшей группе Четырехугольники. Решение задач на готовых чертежах. (8 класс)
Четырехугольники. Решение задач на готовых чертежах. (8 класс) Sequential games. Empirical evidence and bargaining. (Lecture 5)
Sequential games. Empirical evidence and bargaining. (Lecture 5) Множества и функции
Множества и функции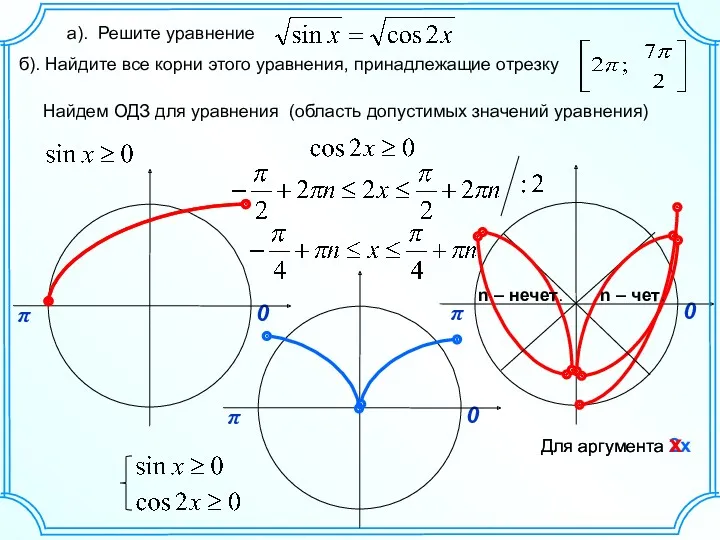 Решение тригонометрического уравнения (С 1, 26)
Решение тригонометрического уравнения (С 1, 26) Проектная деятельность учащихся на уроках математики
Проектная деятельность учащихся на уроках математики Координатный угол
Координатный угол Применение интересных свойств трапеции при решении задач
Применение интересных свойств трапеции при решении задач