Содержание
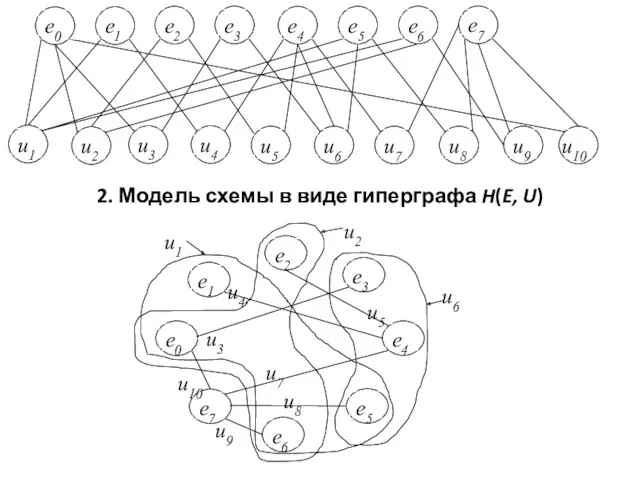
- 2. 2. Модель схемы в виде гиперграфа H(E, U)
- 3. Матрица комплексов Q=||qij||n×k
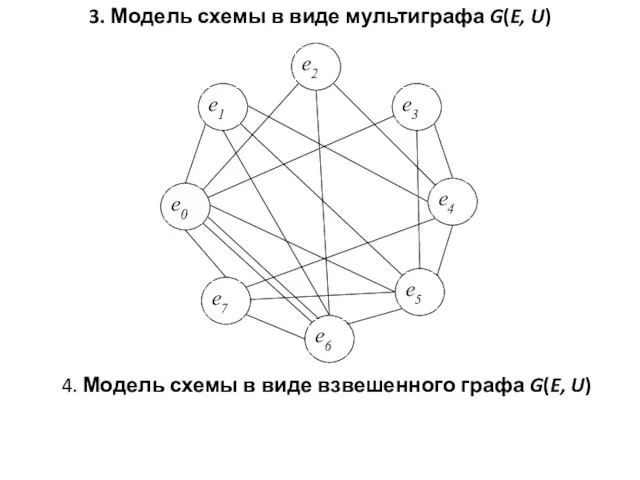
- 4. 3. Модель схемы в виде мультиграфа G(E, U) 4. Модель схемы в виде взвешенного графа G(E,
- 5. Матрица соединений R=||rij||n×n. Матрицу соединений легко получить из матрицы комплексов
- 6. Алгоритмы раскраски графа Необходимо раскрасить вершины графа таким образом, чтобы смежные вершины были окрашены в разные
- 7. 5. Если R ≠ ∅, то переход к п. 2, иначе к п. 6; 1. В
- 8. 10. Составляется конъюнкция П’ = ∧ti. Раскрываются скобки. В полученной дизъюнкции на основе законов булевой алгебры
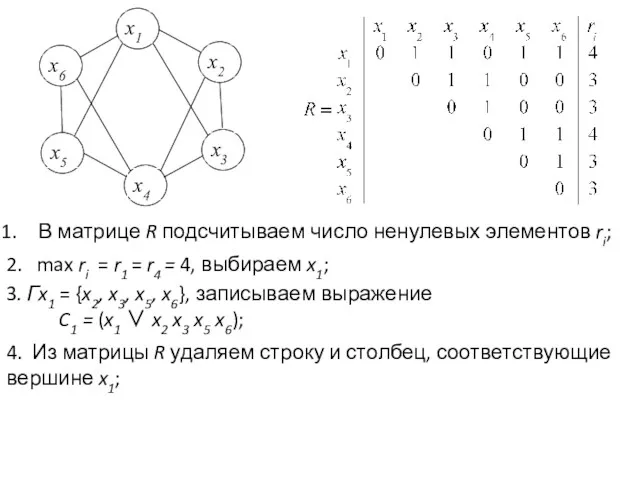
- 9. В матрице R подсчитываем число ненулевых элементов ri; 3. Гx1 = {x2, x3, x5, x6}, записываем
- 10. 5. R ≠ ∅, max ri = r4 = 4; Гx4 = {x2, x3, x5, x6},
- 11. 12. Составляем конъюнкцию Ci и выполняем минимизацию П = ∧Ci = C1 C2 C4 C5 =
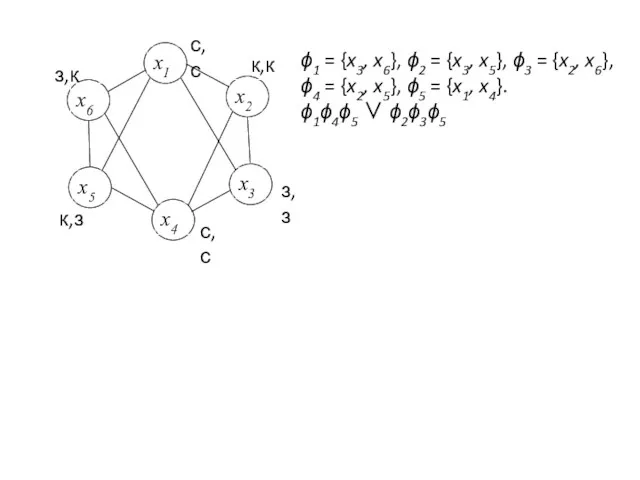
- 12. ϕ1 = {x3, x6}, ϕ2 = {x3, x5}, ϕ3 = {x2, x6}, ϕ4 = {x2, x5},
- 13. Недостатком точных алгоритмов является низкое быстродействие. Поэтому на практике используют приближенные алгоритмы, примером которых может служить
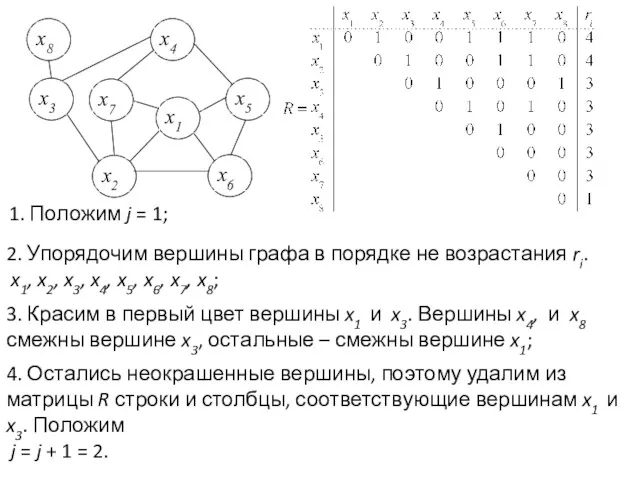
- 14. 1. Положим j = 1; 2. Упорядочим вершины графа в порядке не возрастания ri. x1, x2,
- 15. 5. Упорядочим вершины графа в порядке не возрастания ri: x2, x4, x5, x6, x7, x8; 6.
- 16. Достоинство алгоритма – быстродействие. Недостаток – не оптимальность. Для раскраски вершин графа приближенным алгоритмом потребовалось четыре
- 17. Математическая модель задачи размещения Пусть заданы множество элементов E={e1, e2, …, em} и множество фиксированных позиций
- 18. Алгоритм обратного размещения Алгоритм обратного размещения принадлежит группе алгоритмов параллельно-последовательного размещения. В методе обратного размещения осуществляются
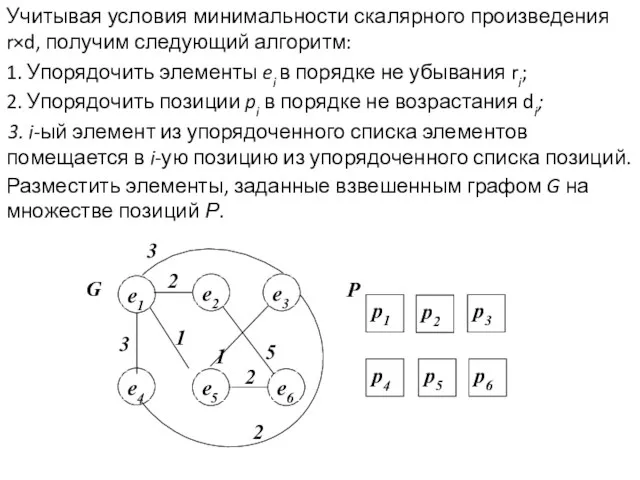
- 19. Учитывая условия минимальности скалярного произведения r×d, получим следующий алгоритм: 1. Упорядочить элементы ei в порядке не
- 20. Составим матрицы соединений R и расстояний D. Упорядочим элементы ei в порядке не убывания ri {e5,
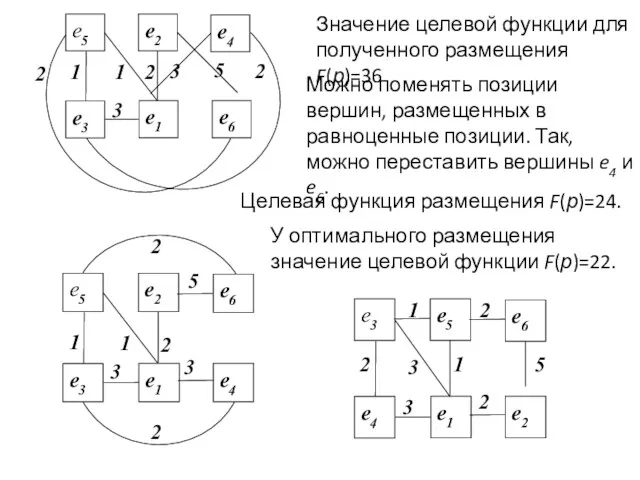
- 21. Значение целевой функции для полученного размещения F(р)=36 Можно поменять позиции вершин, размещенных в равноценные позиции. Так,
- 22. Кратчайшие пути Пусть дан граф G(X, Γ), ребрам которого приписаны веса, заданные матрицей C=||cij||m×m. Задача о
- 23. 1. Положить l(s)=0+ и считать эту пометку постоянной. Положить l(xi)=∞ для всех xi ≠ s и
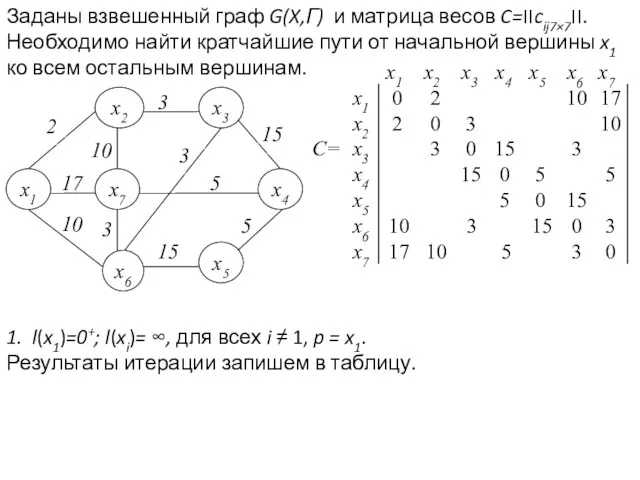
- 24. Заданы взвешенный граф G(X,Г) и матрица весов C=׀׀cij׀׀7×7. Необходимо найти кратчайшие пути от начальной вершины x1
- 25. 2. Гp ={x2, x6, x7} – все пометки временные, уточним их: l(x2)=min[∞ ,0++2]=2; l(x6)=min[∞, 0++10]=10; l(x7)=min[∞,
- 26. 6. l(xi*) = min[l(xi)] = l(x3) = 5. 7. l(x3) = 5+, p=x3. 8. Не все
- 27. 12. l(xi*) = min[l(xi)] = l(x7) = 11. 13. l(x7) = 11+, p=x7. 14. Не все
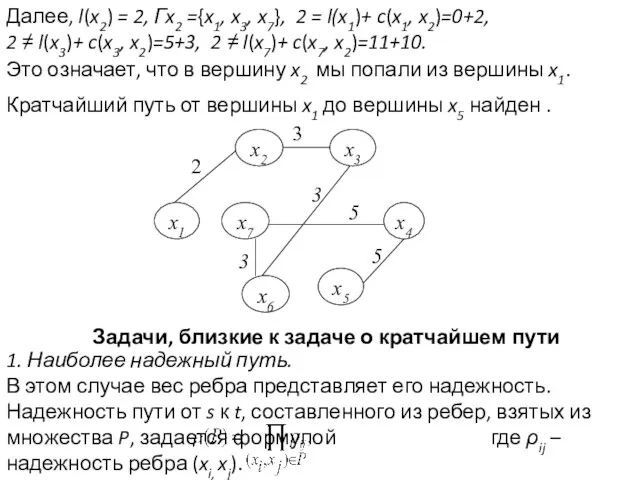
- 28. Кратчайшие расстояния от вершины x1 до всех вершин найдены. Как найти кратчайший путь до конкретной вершины,
- 29. Далее, l(x2) = 2, Гx2 ={x1, x3, x7}, 2 = l(x1)+ c(x1, x2)=0+2, 2 ≠ l(x3)+
- 30. 2. Самый длинный (критический) путь. Задача сетевого планирования, заключающаяся в нахождении самого длинного по временной протяженности
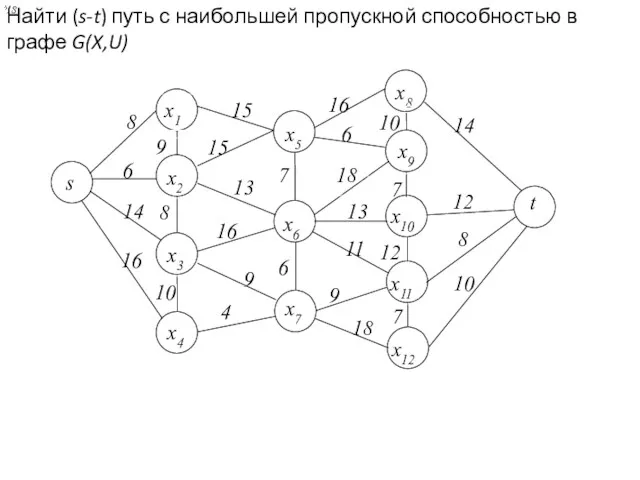
- 31. Теорема Форда – Фалкерсона. Пропускная способность пути с наибольшей пропускной способностью от s к t равна
- 32. Найти (s-t) путь с наибольшей пропускной способностью в графе G(X,U) 18 18
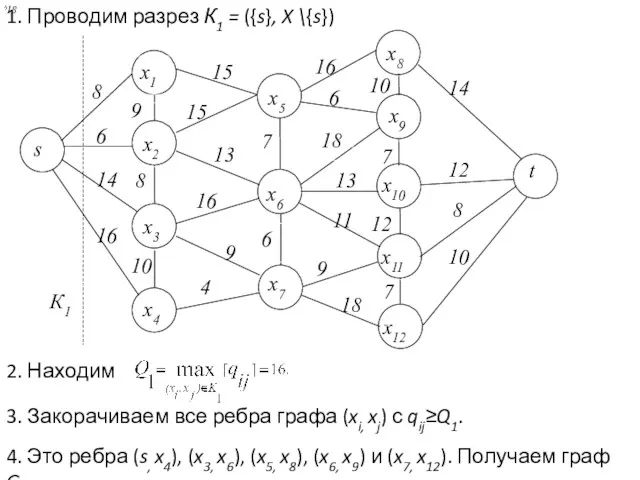
- 33. 1. Проводим разрез К1 = ({s}, X \{s}) 18 2. Находим 3. Закорачиваем все ребра графа
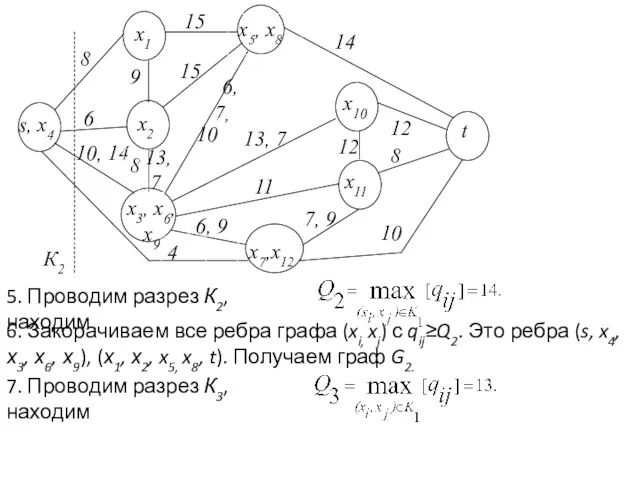
- 34. 5. Проводим разрез К2, находим 6. Закорачиваем все ребра графа (xi, xj) с qij≥Q2. Это ребра
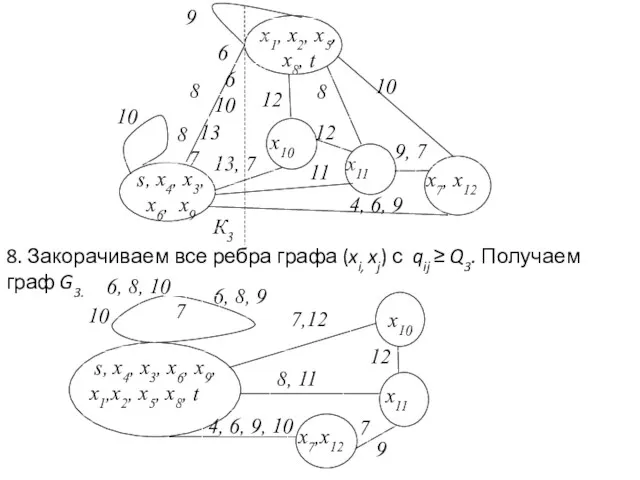
- 35. 8. Закорачиваем все ребра графа (xi, xj) с qij ≥ Q3. Получаем граф G3.
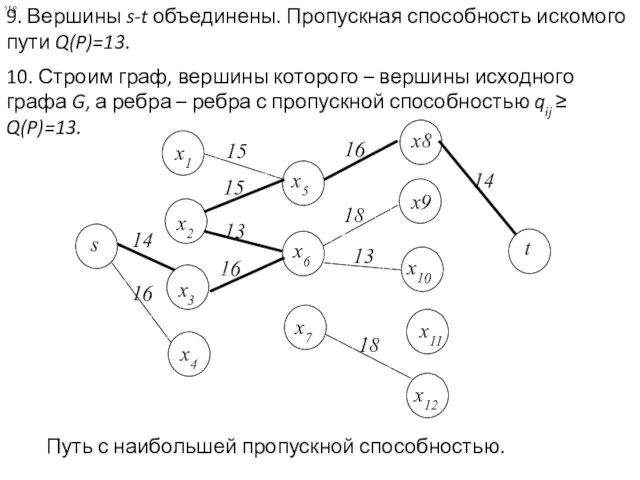
- 36. 9. Вершины s-t объединены. Пропускная способность искомого пути Q(P)=13. 10. Строим граф, вершины которого – вершины
- 38. Скачать презентацию
















![6. l(xi*) = min[l(xi)] = l(x3) = 5. 7. l(x3)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/428673/slide-25.jpg)
![12. l(xi*) = min[l(xi)] = l(x7) = 11. 13. l(x7)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/428673/slide-26.jpg)



 Десятичная запись дробных чисел (5 класс)
Десятичная запись дробных чисел (5 класс) Основні характеристики ТКМ. Лекція 6
Основні характеристики ТКМ. Лекція 6 Ряды
Ряды Первый признак подобия треугольников
Первый признак подобия треугольников Сечение куба, призмы и пирамиды
Сечение куба, призмы и пирамиды Решение показательных неравенств
Решение показательных неравенств Математическое кафе
Математическое кафе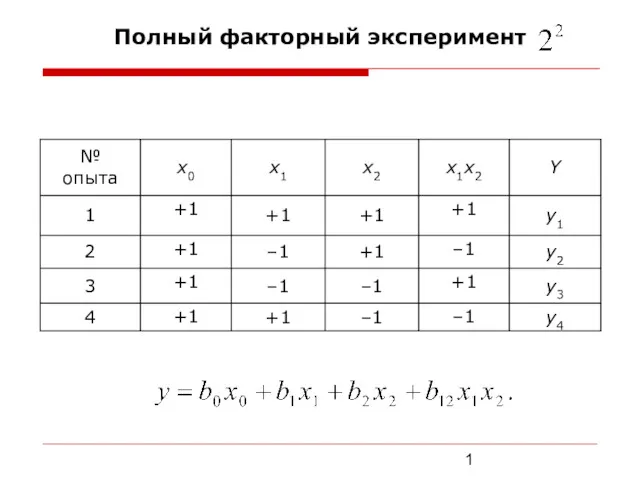 Полный факторный эксперимент
Полный факторный эксперимент презентация по математике на тему Выше или ниже
презентация по математике на тему Выше или ниже Великая теорема Ферма
Великая теорема Ферма Путешествие в сказку. Десятичные дроби
Путешествие в сказку. Десятичные дроби Графы и их представление на ЭВМ
Графы и их представление на ЭВМ Действия с обыкновенными дробями
Действия с обыкновенными дробями Параллельные прямые
Параллельные прямые Логарифмик тигезләмәләр
Логарифмик тигезләмәләр Подготовка к решению задач в два действия (1 класс)
Подготовка к решению задач в два действия (1 класс) Многочлен Р(х) и его корень. Теорема Безу
Многочлен Р(х) и его корень. Теорема Безу Прямоугольный параллелепипед
Прямоугольный параллелепипед Теория вероятностей. События. Виды событий. Вероятностное пространство. Вероятностные схемы: классическая, геометрическая
Теория вероятностей. События. Виды событий. Вероятностное пространство. Вероятностные схемы: классическая, геометрическая Касательная к графику функции
Касательная к графику функции Площадь (тест для учащихся 3-4 классов)
Площадь (тест для учащихся 3-4 классов) Вычитание натуральных чисел
Вычитание натуральных чисел Урок математики Решение уравнений 3 класс УМК Школа России
Урок математики Решение уравнений 3 класс УМК Школа России Логические выражения и уравнения
Логические выражения и уравнения Решение практических задач с помощью производной
Решение практических задач с помощью производной Арифметическая прогрессия (9 класс)
Арифметическая прогрессия (9 класс) Прямоугольный треугольник
Прямоугольный треугольник Квадратные неравенства. Интегрированный урок для учащихся 9 класса
Квадратные неравенства. Интегрированный урок для учащихся 9 класса