Содержание
- 2. Прямоугольная система координат в пространстве Если через точку пространства проведены три попарно перпендикулярные прямые, на каждом
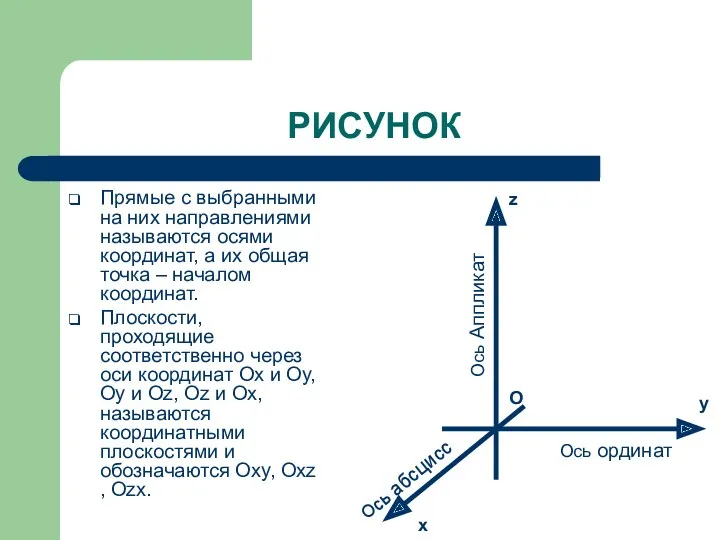
- 3. РИСУНОК Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом
- 4. Определение луча на координатной плоскости. Точка О разделяет каждую из осей координат на два луча. Луч,
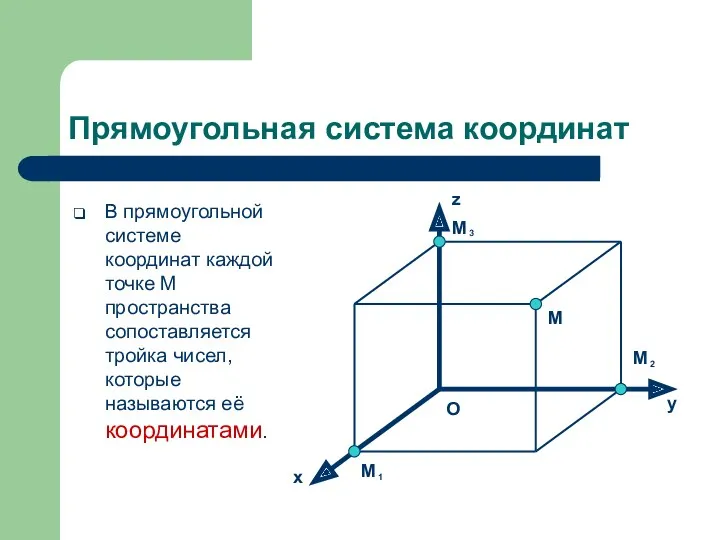
- 5. Прямоугольная система координат В прямоугольной системе координат каждой точке M пространства сопоставляется тройка чисел, которые называются
- 6. Нахождение точки на координатной плоскости. Если, например, точка M лежит на координатной плоскости или на оси
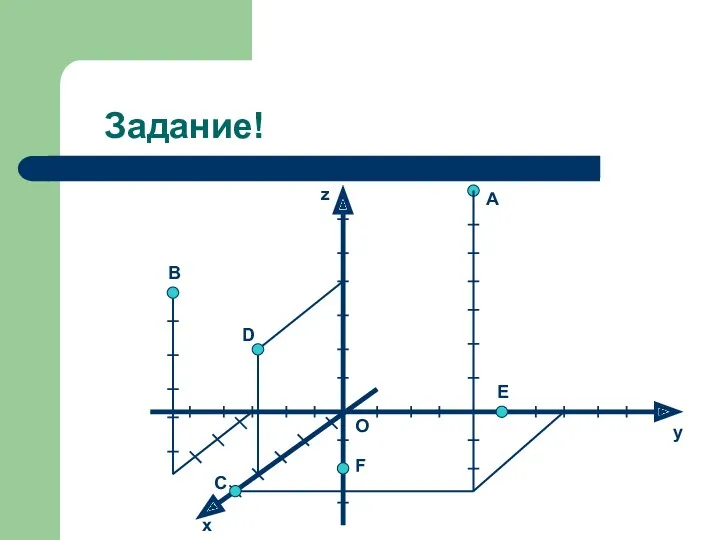
- 7. Задание! B C O E F D z y x A
- 8. Ответы. A(5; 4; 10), B(4; -3; 6), C(5; 0; 0), D(4; 0; 4), E(0; 5; 0),
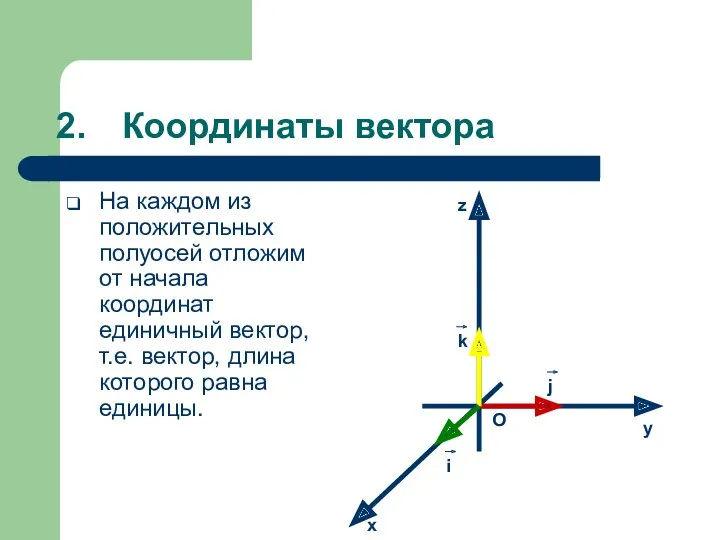
- 9. Координаты вектора На каждом из положительных полуосей отложим от начала координат единичный вектор, т.е. вектор, длина
- 10. Разложение по координатным векторам Любой вектор a можно разложить по координатным векторам, т.е. представить в виде
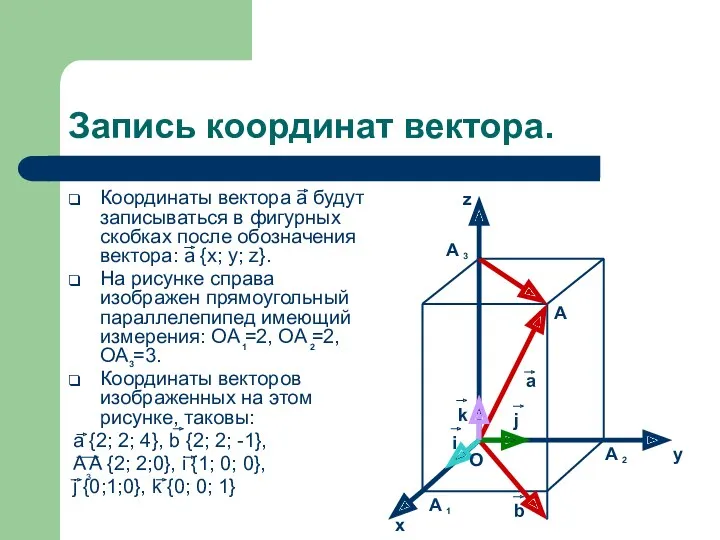
- 11. Запись координат вектора. Координаты вектора а будут записываться в фигурных скобках после обозначения вектора: а {x;
- 12. Нулевой вектор и равные вектора Так как нулевой вектор можно представить в виде 0 = 0i
- 13. Правила нахождения суммы, разности и произведения на данное число. Каждая координата суммы двух или более векторов
- 14. Правило №2 Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Если a {x
- 15. Правило №3 Каждая координата произведения вектора на число равна произведение соответствующей координаты вектора на это число.
- 16. Связь между координатами векторов и координатами точек. Вектор, конец которого совпадает с данной точкой, а начало
- 17. Простейшие задачи в координатах Каждая координата середины отрезка равна полусумме соответствующих координат его концов. Длина вектора
- 18. Расстояние между точками Расстояния между точка M (x ; y ; z ) и M (x
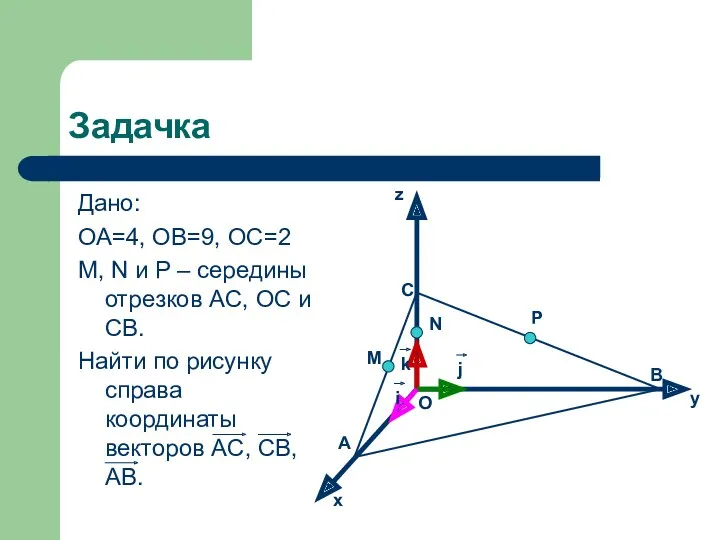
- 19. Задачка Дано: ОА=4, ОВ=9, ОС=2 M, N и P – середины отрезков AC, OC и CB.
- 20. Решение: AC = AO + OC = 4i + 2k, AC {-4; 0; 2} CB =
- 22. Скачать презентацию













 Теорема Пифагора
Теорема Пифагора Окружность и её элементы
Окружность и её элементы Фигуры. Величины
Фигуры. Величины Игровые задания на решение задач в одно действие. Сложение
Игровые задания на решение задач в одно действие. Сложение Загадки листа Мёбиуса
Загадки листа Мёбиуса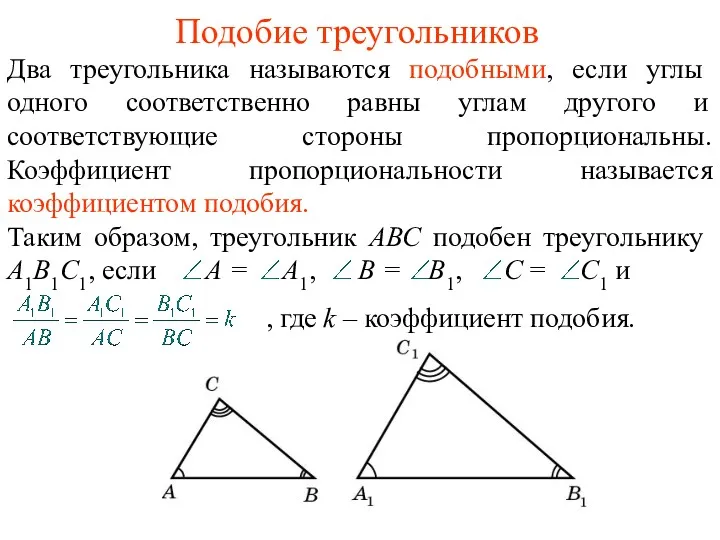 Первый признак подобия треугольников
Первый признак подобия треугольников Показательная функция, её свойства и график
Показательная функция, её свойства и график Сложение положительных и отрицательных чисел
Сложение положительных и отрицательных чисел Масштаб. 6 класс
Масштаб. 6 класс Теорема Пифагора
Теорема Пифагора Второй признак равенства треугольника
Второй признак равенства треугольника 02
02 Модели управления запасами
Модели управления запасами Решение квадратных неравенств. 8 класс
Решение квадратных неравенств. 8 класс Скалярное произведение векторов
Скалярное произведение векторов Решение примеров с переходом через десяток. + 4.
Решение примеров с переходом через десяток. + 4. Подготовка к ГИА по математике. Задания 4
Подготовка к ГИА по математике. Задания 4 Случаи сложения вида +7
Случаи сложения вида +7 Графики зависимости кинематических величин от времени при равномерном и равноускоренном движении
Графики зависимости кинематических величин от времени при равномерном и равноускоренном движении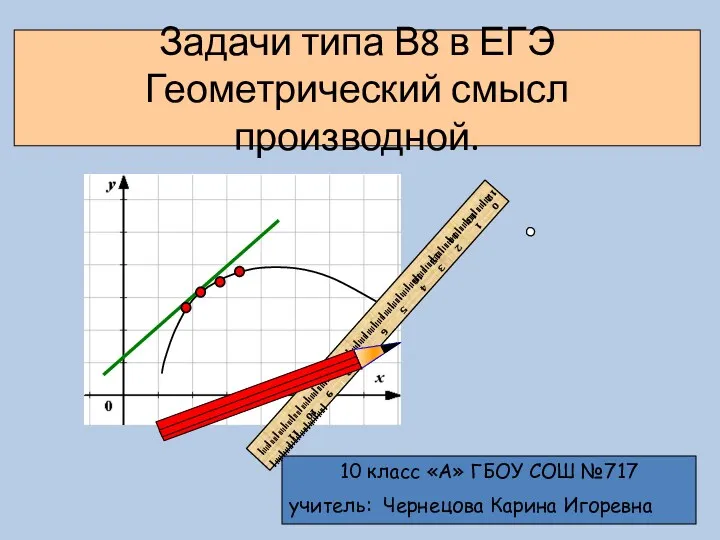 Геометрический смысл производной. Задачи типа В8 в ЕГЭ
Геометрический смысл производной. Задачи типа В8 в ЕГЭ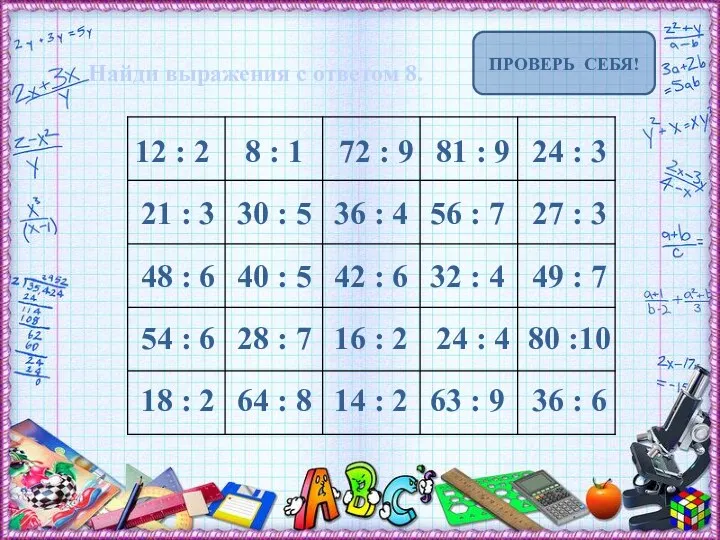 Тренажёр Найди выражения с ответом 8
Тренажёр Найди выражения с ответом 8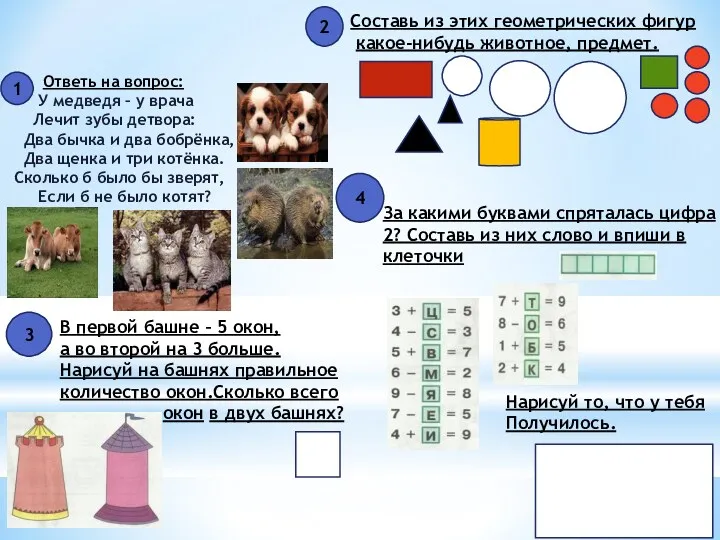 Занимательная математика в первом классе.
Занимательная математика в первом классе. Фиктивные переменные в регрессионных моделях
Фиктивные переменные в регрессионных моделях Скалярное произведение векторов
Скалярное произведение векторов Задачи на построение. Окружность. Урок 2
Задачи на построение. Окружность. Урок 2 Признаки делимости
Признаки делимости Методологические проблемы применения математических методов в психологии. (Лекция 1)
Методологические проблемы применения математических методов в психологии. (Лекция 1) Математические фокусы
Математические фокусы