Содержание
- 2. Параметрические и непараметрические критерии Такие статистические критерии, как z, t и F называются параметрическими. Параметрические критерии
- 3. 9.1. Критерий Вилкоксона Wilcoxon Rank-Sum Test for Two Independent Samples
- 4. Что проверяет критерий Вилкоксона Критерий Вилкоксона проверяет гипотезу об однородности для двух независимых выборок: совпадают ли
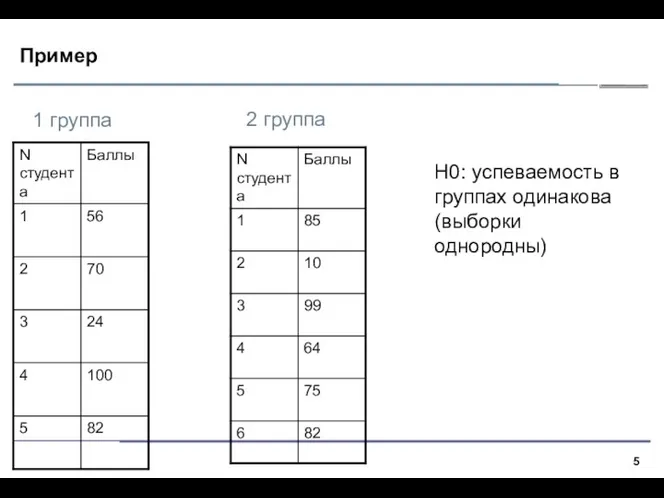
- 5. Пример 1 группа 2 группа H0: успеваемость в группах одинакова (выборки однородны)
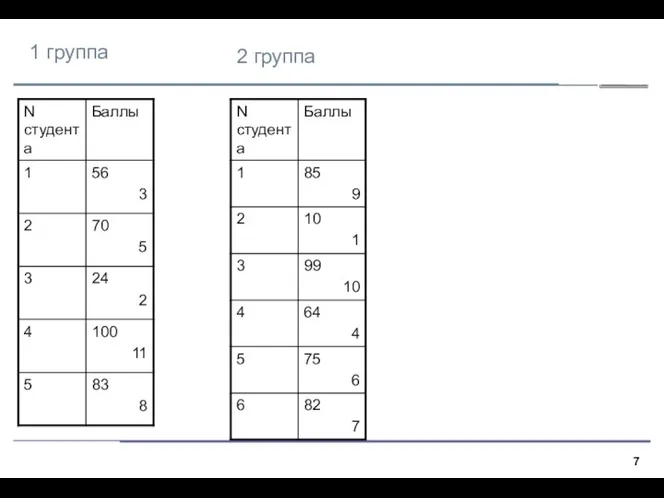
- 6. Последовательность действий Шаг 1. Объединяем две выборки и находим ранги каждого наблюдения в объединенной выборке. Ранг
- 7. 1 группа 2 группа
- 8. Последовательность действий Шаг 2. Найдем сумму рангов первой и сумму рангов второй выборки. Если выборки однородны,
- 9. Последовательность действий Шаг 2. Найдем сумму рангов первой и сумму рангов второй выборки (R и S).
- 10. Последовательность действий Шаг 3. Вычислим статистику: если n≤10, статистика W есть сумма рангов первой выборки R.
- 11. Последовательность действий Шаг 3. Вычислим статистику: если n>10, статистика есть: есть среднее значение R, при условии,
- 12. Последовательность действий Шаг 3. Вычислим статистику: если n>10, статистика есть:
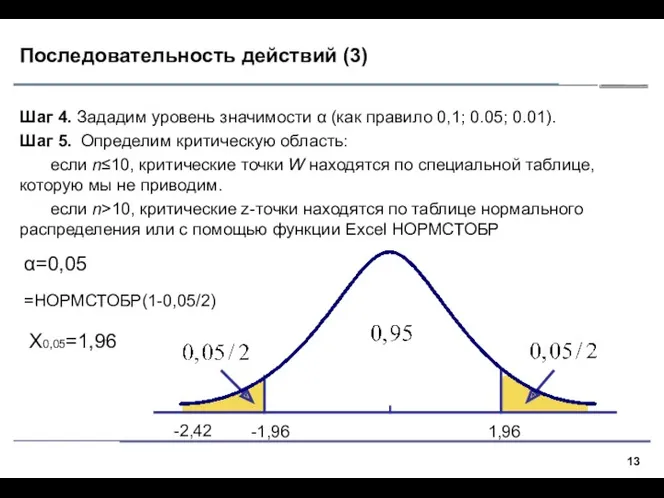
- 13. Последовательность действий (3) Шаг 4. Зададим уровень значимости α (как правило 0,1; 0.05; 0.01). Шаг 5.
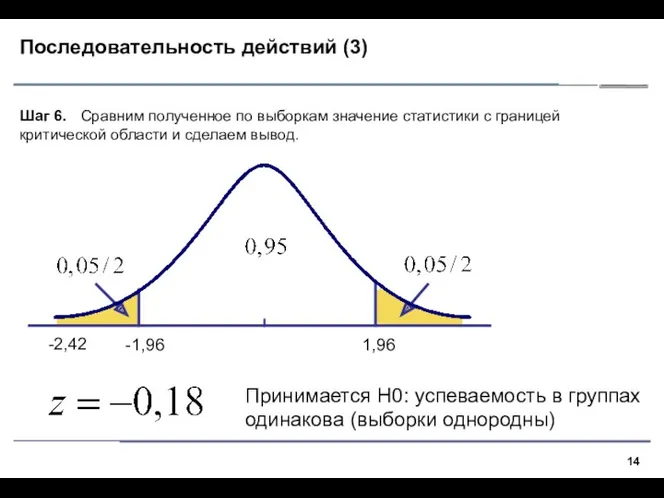
- 14. Последовательность действий (3) Шаг 6. Сравним полученное по выборкам значение статистики с границей критической области и
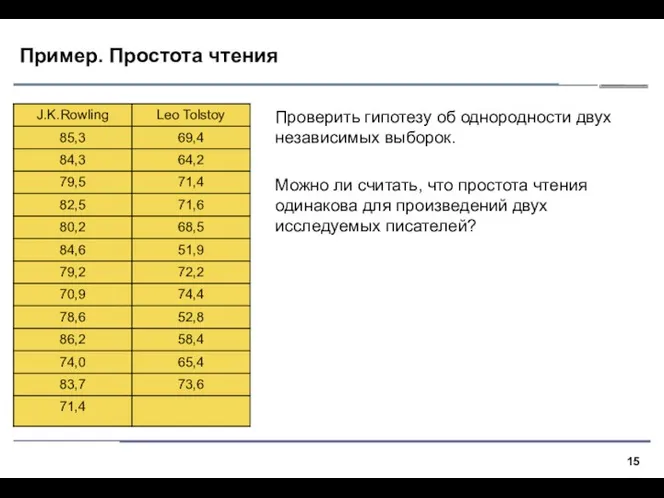
- 15. Пример. Простота чтения Проверить гипотезу об однородности двух независимых выборок. Можно ли считать, что простота чтения
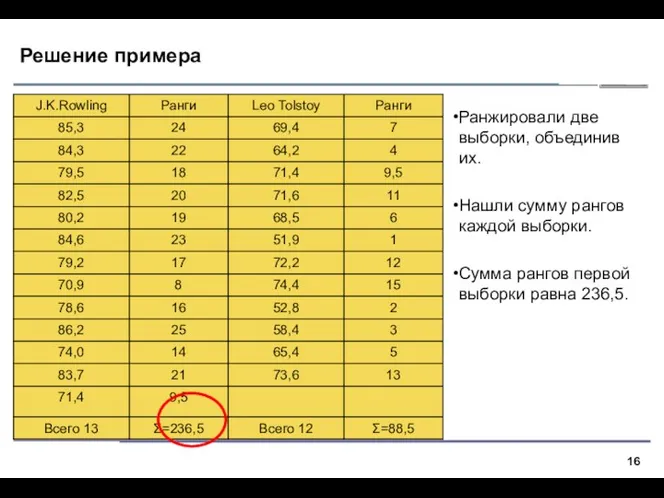
- 16. Решение примера Ранжировали две выборки, объединив их. Нашли сумму рангов каждой выборки. Сумма рангов первой выборки
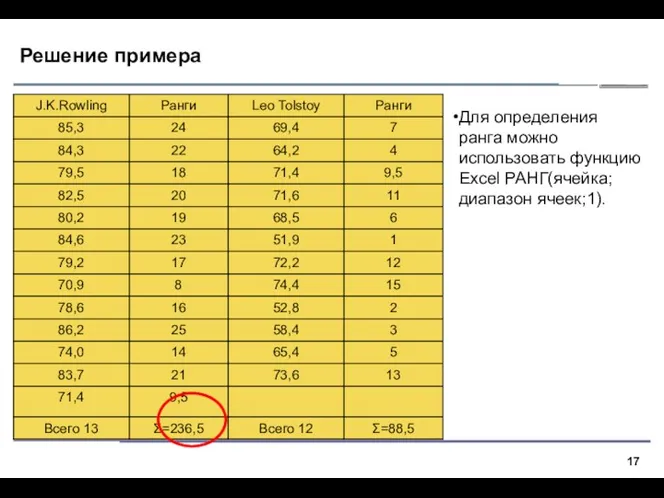
- 17. Решение примера Для определения ранга можно использовать функцию Excel РАНГ(ячейка;диапазон ячеек;1).
- 18. Вычисления Находим следующие величины:
- 19. Получение вывода Критическая область является двусторонней и при α=0.05 критические точки z=-1,96 и z=-1,96. Полученное нами
- 20. 9.2. Однофакторный непараметрический критерий Краскела-Уоллиса Kruskal-Wallis Test
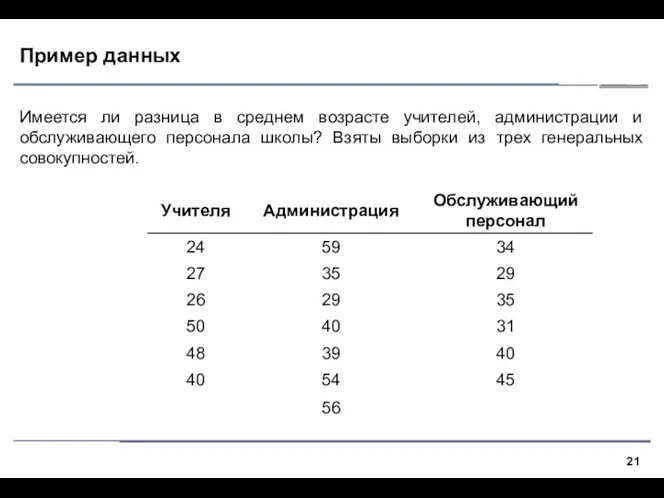
- 21. Пример данных Имеется ли разница в среднем возрасте учителей, администрации и обслуживающего персонала школы? Взяты выборки
- 22. Критерий Краскела-Уоллиса В дисперсионном анализе используется F-критерий, чтобы сравнивать средние трех и более совокупностей. Для критерия
- 23. Условия применения Выборки независимы и получены случайным образом. Размер каждой выборки должен быть не меньше пяти.
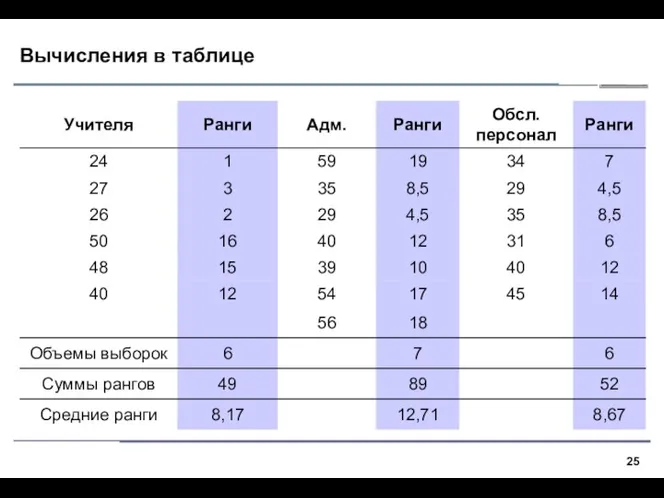
- 24. Суть критерия 1. В критерии Краскела–Уоллиса все выборки объединяются и значения ранжируются. Далее вычисляются средние ранги
- 25. Вычисления в таблице
- 26. Статистика Формула статистики Краскела-Уоллиса: где: – средние ранги выборок (i = 1,2,3,…,k) – средний ранг по
- 27. Вычисляем значение статистики
- 28. Критическая область Критерий использует правостороннюю критическую область. Если выполнена нулевая гипотеза однородности, то статистика H имеет
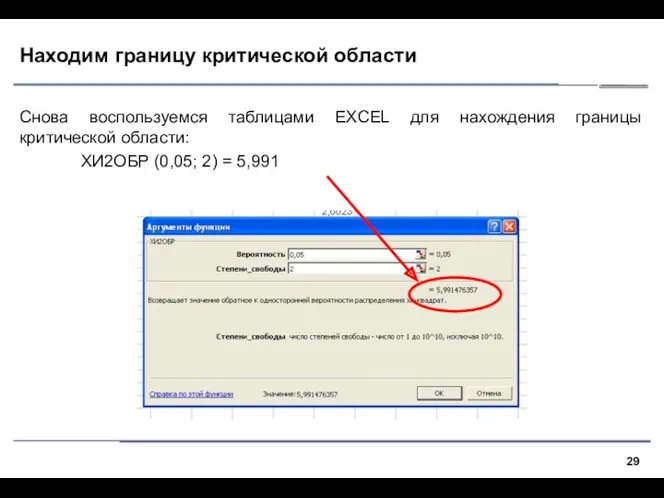
- 29. Находим границу критической области Снова воспользуемся таблицами EXCEL для нахождения границы критической области: ХИ2ОБР (0,05; 2)
- 30. Сравниваем и делаем вывод Полученное значение статистики не попало в критическую область: Вывод. Мы не имеем
- 31. 9.3. Коэффициент корреляции Спирмена Проверка связи для порядковых переменных
- 32. Две порядковые переменные Порядковая шкала означает, что категории могут быть упорядочены по возрастанию. Пример. Отметки по
- 33. Если есть полная связь? Полная связь между признаками означает, что для любых двух объектов если r1
- 34. Постановка проблемы Полная связь между признаками встречается редко! Однако, значения двух признаков могут быть пусть и
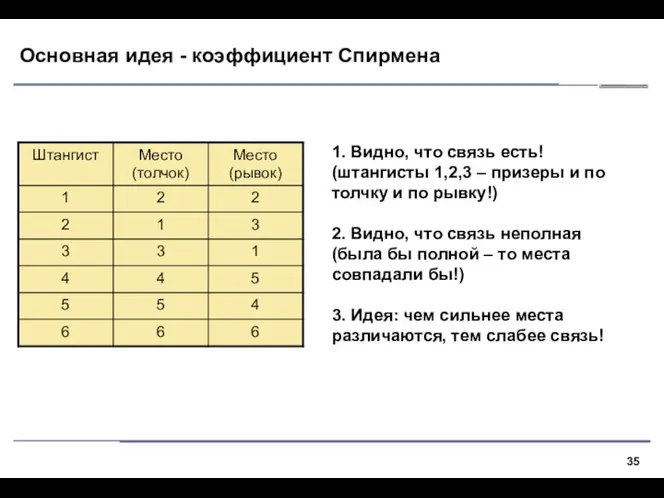
- 35. Основная идея - коэффициент Спирмена 1. Видно, что связь есть! (штангисты 1,2,3 – призеры и по
- 36. Понятие рангового коэффициента корреляции Предположим, что для n объектов измерены 2 порядковых признака. - ранги объектов
- 37. Коэффициент ранговой корреляции Спирмена можно вычислить и по более простой формуле:
- 38. Свойства рангового коэффициента корреляции 1. Для совпадающих ранжировок r = 1 (очевидно). 2. Для противоположных ранжировок
- 39. Корреляционный анализ порядковых признаков Иногда проводят преобразование количественного признака в порядковый значения количественного признака для n
- 40. Свойства рангового коэффициента корреляции 3. Если ранги строились по количественным признакам и где f – возрастающая
- 41. Свойства рангового коэффициента корреляции 4. Если ранги строились по количественным признакам и где f – убывающая
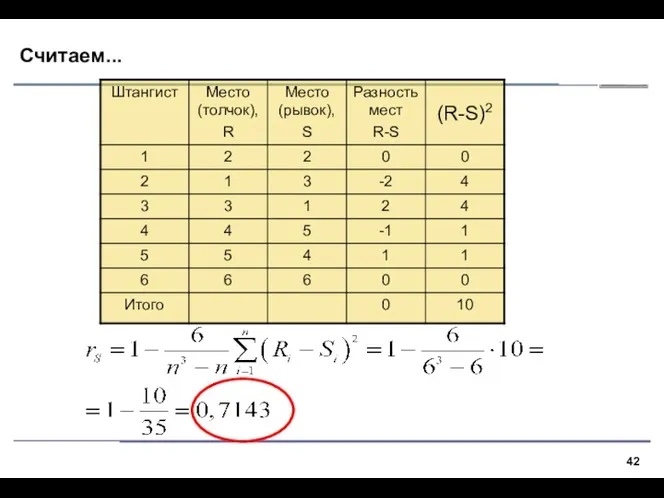
- 42. Считаем...
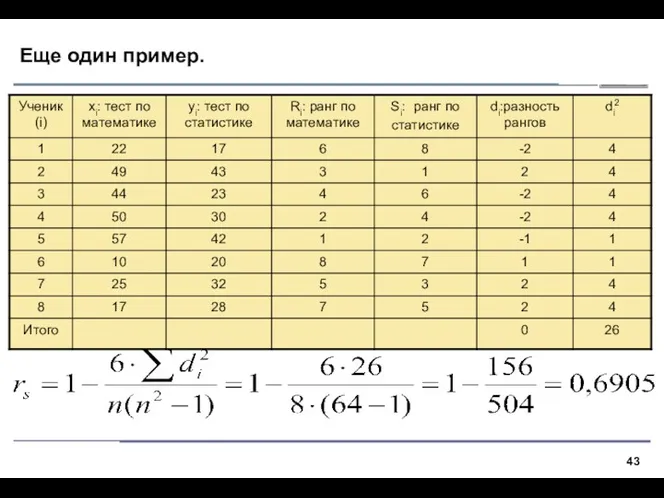
- 43. Еще один пример.
- 44. Проверка значимости рангового коэффициента корреляции Обозначения: Выборочный коэффициент корреляции Спирмена rs Коэффициент корреляции генеральной совокупности ρs
- 45. Проверка значимости рангового коэффициента корреляции Если исходные порядковые признаки независимы, то статистика близка к 0. Для
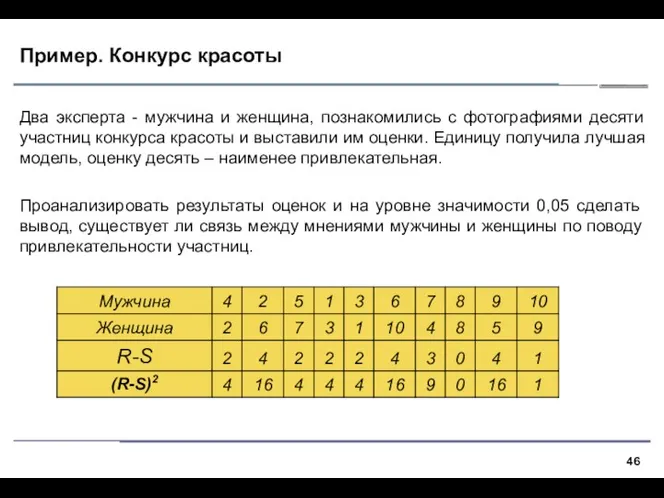
- 46. Пример. Конкурс красоты Два эксперта - мужчина и женщина, познакомились с фотографиями десяти участниц конкурса красоты
- 47. Решение. Сумма квадратов разностей рангов равна 74. Вычисляем коэффициент ранговой корреляции Спирмена: Вычисляем статистику
- 49. Скачать презентацию
































 Презентация к уроку математики на тему: Случаи сложения вида 26+4. Переход через разряд 2 класс
Презентация к уроку математики на тему: Случаи сложения вида 26+4. Переход через разряд 2 класс Письменное деление на трёхзначное число
Письменное деление на трёхзначное число Тест Нумерация четырёхзначных чисел
Тест Нумерация четырёхзначных чисел Скалярное произведение векторов
Скалярное произведение векторов Ученые, изучавшие многогранники
Ученые, изучавшие многогранники Сложение и вычитание десятичных дробей. Урок математики в 5 классе
Сложение и вычитание десятичных дробей. Урок математики в 5 классе Повторение курса математики 5 класса
Повторение курса математики 5 класса Презентация к уроку по теме Теорема Пифагора
Презентация к уроку по теме Теорема Пифагора Урок математики Решение уравнений 2 класс
Урок математики Решение уравнений 2 класс Дидактическая игра Большой, средний, маленький
Дидактическая игра Большой, средний, маленький Скалярное произведение векторов. 9 класс
Скалярное произведение векторов. 9 класс Периметр прямоугольника, квадрата, произвольного многоугольника
Периметр прямоугольника, квадрата, произвольного многоугольника Скалярное произведение векторов. Вычисление углов между прямыми
Скалярное произведение векторов. Вычисление углов между прямыми Формулы сокращенного умножения
Формулы сокращенного умножения Деление дробей. Задание для устного счета. Упражнение 14. 6 класс
Деление дробей. Задание для устного счета. Упражнение 14. 6 класс Развёртка прямоугольного параллелепипеда. Урок 142
Развёртка прямоугольного параллелепипеда. Урок 142 Правило округления чисел
Правило округления чисел Тест по математике Решение логических задач. 5 класс
Тест по математике Решение логических задач. 5 класс Алгебраические дроби
Алгебраические дроби Confidence interval and Hypothesis testing for population mean (µ) when is known and n (large)
Confidence interval and Hypothesis testing for population mean (µ) when is known and n (large) Решение задач с применением диаграмм Эйлера-Венна
Решение задач с применением диаграмм Эйлера-Венна Конус. Властивості конуса
Конус. Властивості конуса Решение задач в 1-ом классе
Решение задач в 1-ом классе Действия с десятичными дробями. 5 класс
Действия с десятичными дробями. 5 класс Математика – царица наук. 5 класс
Математика – царица наук. 5 класс Урок обобщения и систематизации знаний о прогрессии. 9 класс
Урок обобщения и систематизации знаний о прогрессии. 9 класс Площадь параллелограмма. Открытый урок в 8 классе
Площадь параллелограмма. Открытый урок в 8 классе Нормальный алгоритм Маркова. Лекция №4
Нормальный алгоритм Маркова. Лекция №4