Содержание
- 2. Определения. Основные термины. Свойства определенного интеграла.
- 3. Определение: Под определенным интегралом от данной непрерывной функции на данном отрезке понимается соответствующее приращение ее первообразной,
- 4. Теорема 1: (из теоремы Коши-всякая непрерывная функция на отрезке имеет первообразную) Для всякой функции, непрерывной на
- 5. Свойства: 1.
- 6. 2.
- 7. 3.
- 8. Если непрерывна на ; ; , то 4
- 9. 5.
- 10. 6. Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных
- 11. 8. Если и , то
- 12. 9. Теорема о среднем: - непрерывная функция · , где
- 13. Геометрический смысл определенного интеграла. Теорема: Определенный интеграл от непрерывной неотрицательной функции при равен площади соответствующей криволинейной
- 14. Определенный интеграл с переменным верхним пределом Производная определенного интеграла с переменным верхним пределом по этому пределу
- 15. Интегрирование по частям в определенном интеграле
- 16. Замена переменной в определенном интеграле. Введем новую переменную , ,
- 17. Площадь в прямоугольных координатах. 1.Рассмотрим криволинейную трапецию, ограниченную линиями , , , .
- 18. 2.В более сложных случаях фигуру стараются представить в виде суммы или разности криволинейных трапеций.
- 19. Длина дуги. Определение: Под длиной дуги АВ понимается предел, к которому стремится длина ломанной линии, вписанной
- 20. Определение: Назовем кривую гладкой, если функция, задающая кривую, непрерывна и имеет непрерывную производную.
- 21. Теорема 1: Всякая гладкая кривая имеет определенную конечную длину дуги.
- 22. Тeорема 2: Дифференциал дуги в прямоугольных координатах равен :
- 23. Объем тела вращения. 1.
- 24. 2. ;
- 25. Несобственные интегралы Если нарушается хотя бы одно из условий, то называется несобственным интегралом.
- 27. Скачать презентацию



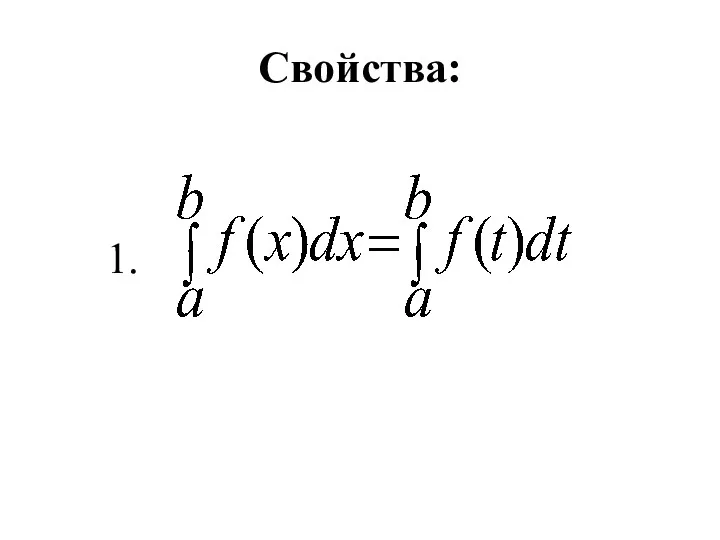
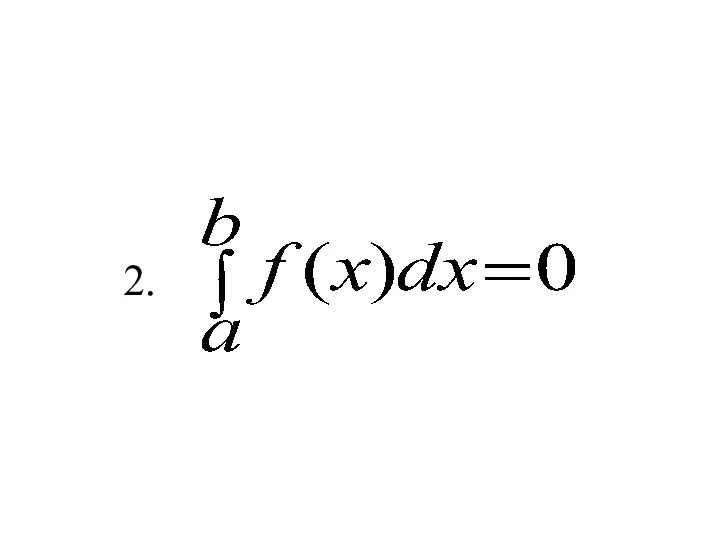
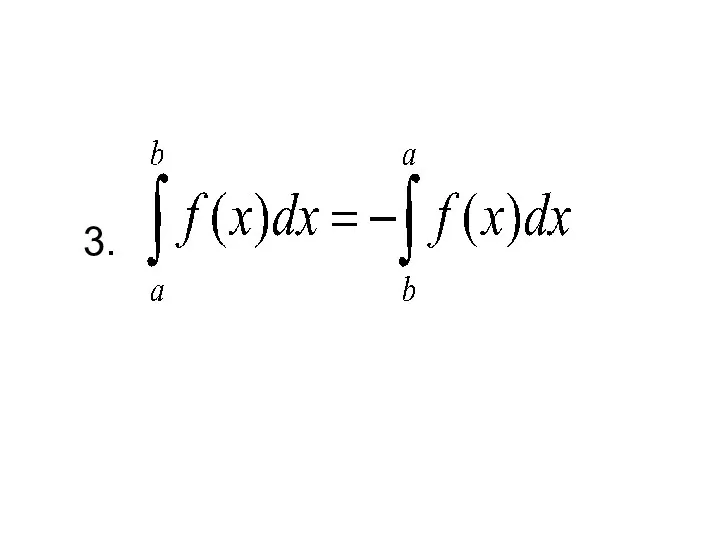
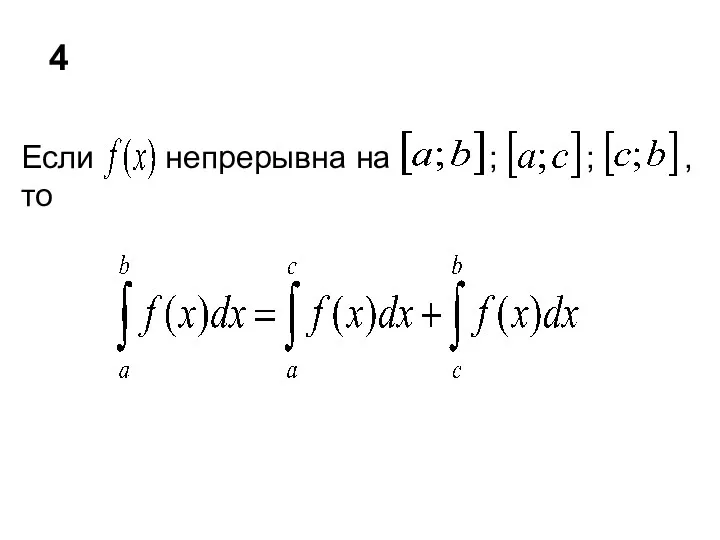
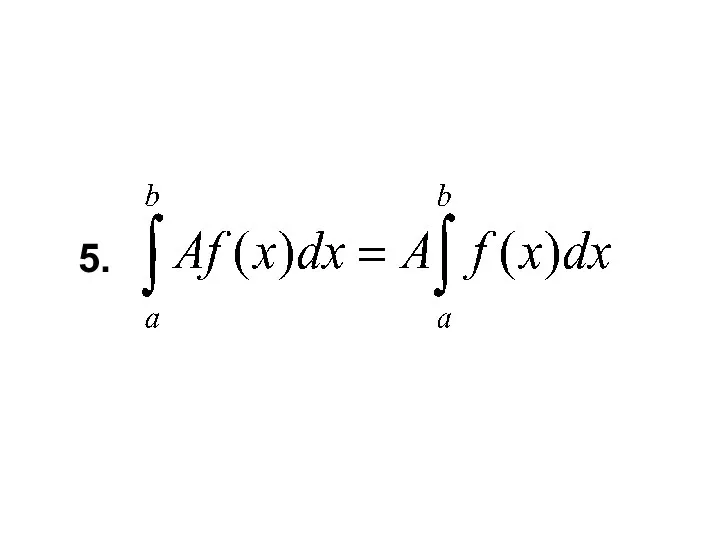

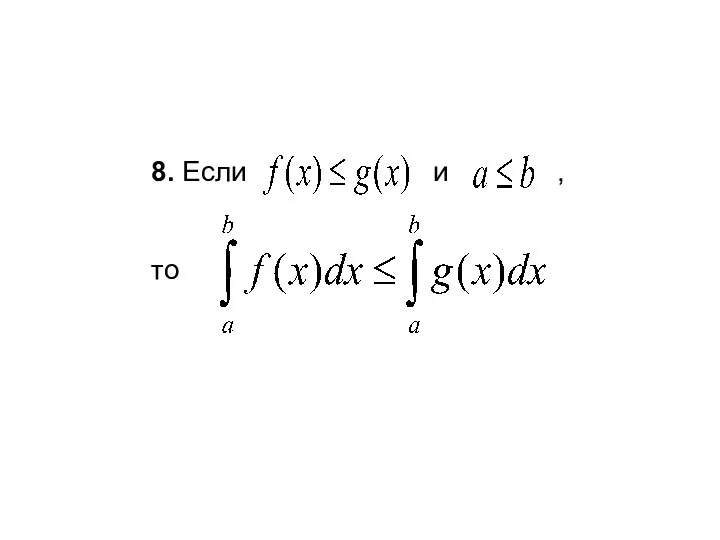



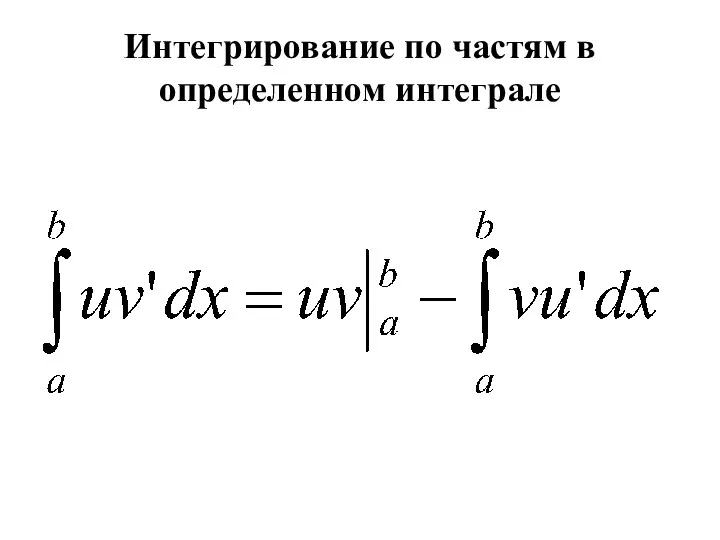








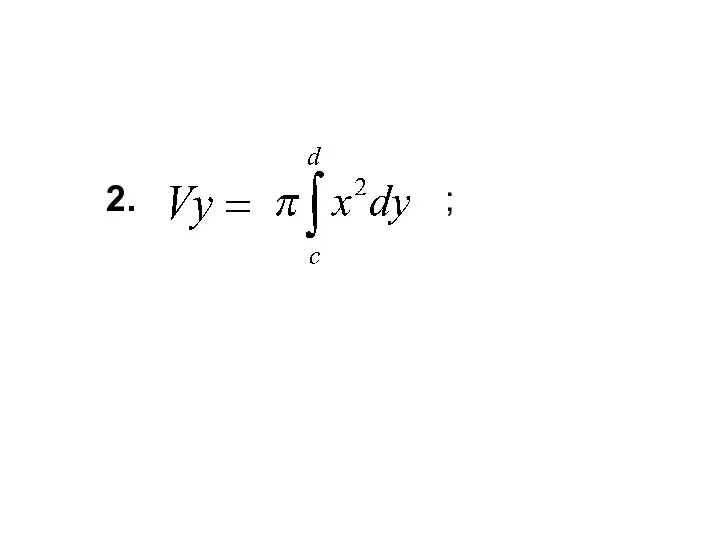

 Статистические гипотезы и достоверность статистических характеристик
Статистические гипотезы и достоверность статистических характеристик Пропорция. Решение задач на проценты с помощью пропорций
Пропорция. Решение задач на проценты с помощью пропорций Подготовка учащихся 8 класса к ГИА по алгебре
Подготовка учащихся 8 класса к ГИА по алгебре CENG 789 – Digital Geometry Processing
CENG 789 – Digital Geometry Processing Презентация к занятию Математический КВН
Презентация к занятию Математический КВН Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии Вычитание смешанных чисел с переходом через единицу
Вычитание смешанных чисел с переходом через единицу Додавання виду 45 + 3 (ознайомлення). Знаходження невідомого доданка. Аналіз умови задачі. Урок №116
Додавання виду 45 + 3 (ознайомлення). Знаходження невідомого доданка. Аналіз умови задачі. Урок №116 1 класс математика Устные вычисления
1 класс математика Устные вычисления Знаходження невідомого зменшуваного
Знаходження невідомого зменшуваного Урок математики Сложение и вычитание двузначных чисел.
Урок математики Сложение и вычитание двузначных чисел. Решение уравнений
Решение уравнений Прямоугольник. 5 класс
Прямоугольник. 5 класс Обходы графов
Обходы графов Умножение вектора на число
Умножение вектора на число Алгоритмы и вычислительные методы оптимизации (установочная лекция)
Алгоритмы и вычислительные методы оптимизации (установочная лекция) Начальные геометрические сведения. Прямая и отрезок
Начальные геометрические сведения. Прямая и отрезок Двугранные углы
Двугранные углы Вычисление количеств по процентам
Вычисление количеств по процентам Математический тренажер Спасибо за шишку
Математический тренажер Спасибо за шишку Проекцияларды өзгерту әдістері
Проекцияларды өзгерту әдістері Метод математической индукции
Метод математической индукции фоны презентаций Диск Диск Диск Диск Диск
фоны презентаций Диск Диск Диск Диск Диск Наименьшее общее кратное и наибольший общий делитель
Наименьшее общее кратное и наибольший общий делитель урок в 1 классе Ломаная
урок в 1 классе Ломаная Трапеция. 8 класс
Трапеция. 8 класс Задачи на готовых чертежах
Задачи на готовых чертежах Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел