в решении диофантовых уравнений с целыми коэффициентами для этого необходимо:
- найти наибольший общий делитель коэффициентов при неизвестных ;
попробовать сократить на него обе части уравнения (разумеется, свободный член должен при этом остаться целым числом).
Второй метод заключается в изображении всех решений на тригонометрической окружности и исключении неподходящих решений.
Метод этот очень прост в применении, если решения легко изобразить на тригонометрической окружности.
Решая тригонометрические уравнения , возникает вопрос отбора корней ,связанных с областью определения и другими условиями.
Рассмотрим пример : 21k - 24n = 8 и решим его первым способом.
Набольший общий делитель коэффициентов равен 3, и сократить его не удается, так как 8 на 3 не делится. Тогда можно сразу сказать, что это уравнение решений в целых числах не имеет.
 Электрорадиоизмерения и метрология. Урок №5. Тема 1.3. Средства измерений
Электрорадиоизмерения и метрология. Урок №5. Тема 1.3. Средства измерений Перпендикуляр и наклонные
Перпендикуляр и наклонные Комбинаторика. Перестановки. Дискретный анализ. Лекция 3
Комбинаторика. Перестановки. Дискретный анализ. Лекция 3 Построение графиков гармонических колебаний
Построение графиков гармонических колебаний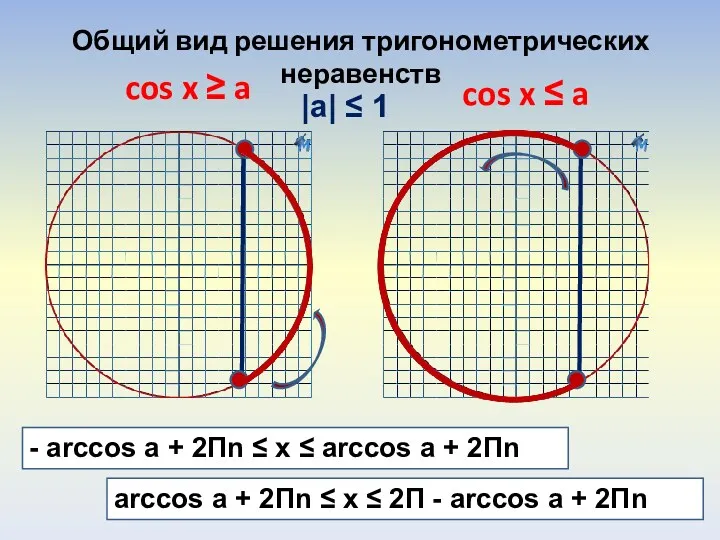 Общий вид решения тригонометрических неравенств
Общий вид решения тригонометрических неравенств Внеклассное мероприятие по математике в 5 классе
Внеклассное мероприятие по математике в 5 классе Категорія Загальні питання. Викторина
Категорія Загальні питання. Викторина Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Умножение обыкновенных дробей
Умножение обыкновенных дробей Метрология. Результаты измерений и их обработка
Метрология. Результаты измерений и их обработка Сфера и шар. Решение задач
Сфера и шар. Решение задач Действия с десятичными дробями произвольного знака
Действия с десятичными дробями произвольного знака Графический способ решения систем уравнений. Алгебра 7 класс
Графический способ решения систем уравнений. Алгебра 7 класс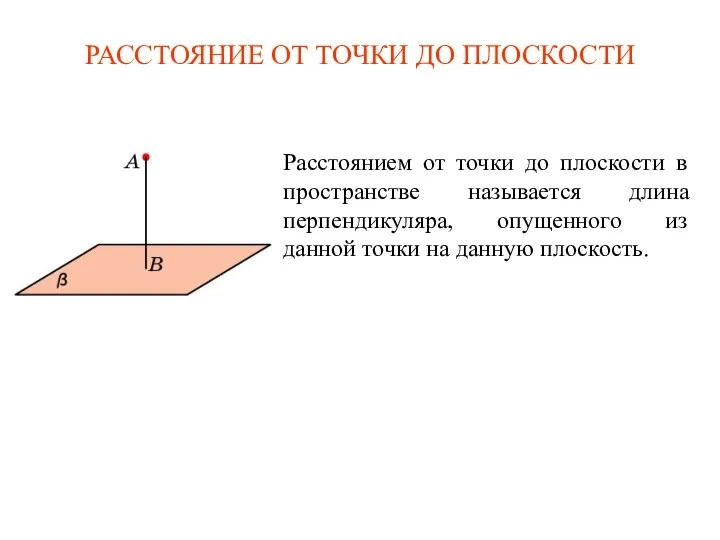 Расстояние от точки до плоскости в пространстве
Расстояние от точки до плоскости в пространстве Математикалық анализге кіріспе. Лекция 8
Математикалық анализге кіріспе. Лекция 8 Скалярное произведение в координатах
Скалярное произведение в координатах Графики. Тест
Графики. Тест число и цифра 7 УМК Л.В.Занков
число и цифра 7 УМК Л.В.Занков Графический метод решения уравнений и неравенств
Графический метод решения уравнений и неравенств Действия с десятичными дробями (5 класс)
Действия с десятичными дробями (5 класс) Обыкновенные дроби. Выполните действия
Обыкновенные дроби. Выполните действия Простой процентный рост
Простой процентный рост Математика и музыка - два полюса человеческой культуры
Математика и музыка - два полюса человеческой культуры Паралельне проектування і його властивості. Зображення фігур у стереометрії
Паралельне проектування і його властивості. Зображення фігур у стереометрії Игра для учащихся Математический активизатор
Игра для учащихся Математический активизатор 7, 8, 0 цифрларын пайдалана отырып, барынша үш таңбалы сандарды жазыңдар
7, 8, 0 цифрларын пайдалана отырып, барынша үш таңбалы сандарды жазыңдар Центральная и осевая симметрия
Центральная и осевая симметрия Конспект урока по математике 4 класс Школа России Письменное деление
Конспект урока по математике 4 класс Школа России Письменное деление