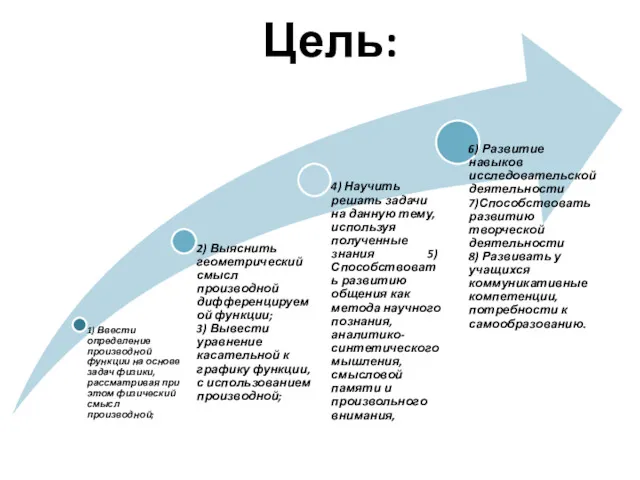
2. ЗАДАЧА О СКОРОСТИ ХИМИЧЕСКОЙ РЕАКЦИИ
Пусть некоторое вещество вступает в
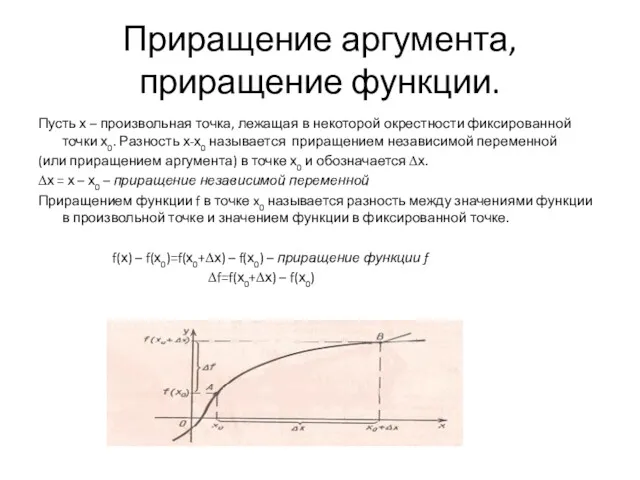
химическую реакцию. Количество этого вещества Q изменяется в течение реакции в зависимости от времени t и является функцией от времени. Пусть за время ∆t количество вещества изменяется на ∆Q , тогда отношение будет выражать среднюю скорость химической реакции за время ∆t, а предел этого отношения
- скорость химической реакции в данный момент
времени t.
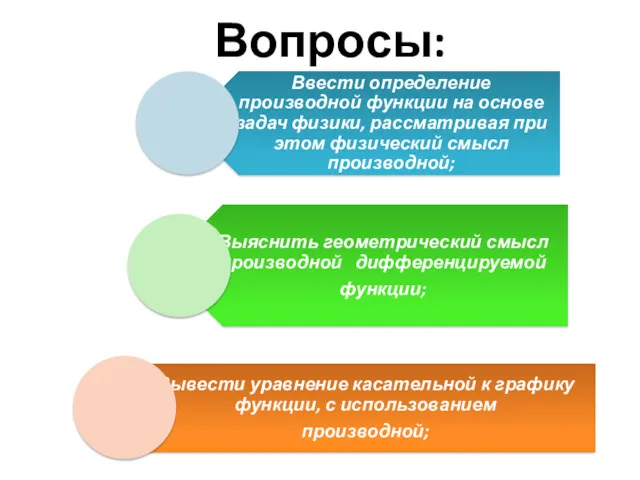
3. ЗАДАЧА ОПРЕДЕЛЕНИЯ СКОРОСТИ РАДИОАКТИВНОГО РАСПАДА
Если m- масса радиоактивного вещества и t- время, то явление радиоактивного распада в момент времени t при условии, что масса радиоактивного вещества с течением времени уменьшается, характеризуется функцией m= m(t).
Средняя скорость распада за время ∆t выражается отношением
а мгновенная скорость распада в момент времени t
.







 Arvutusülesanded ühe osaleva aine järgi
Arvutusülesanded ühe osaleva aine järgi Среднее арифметическое
Среднее арифметическое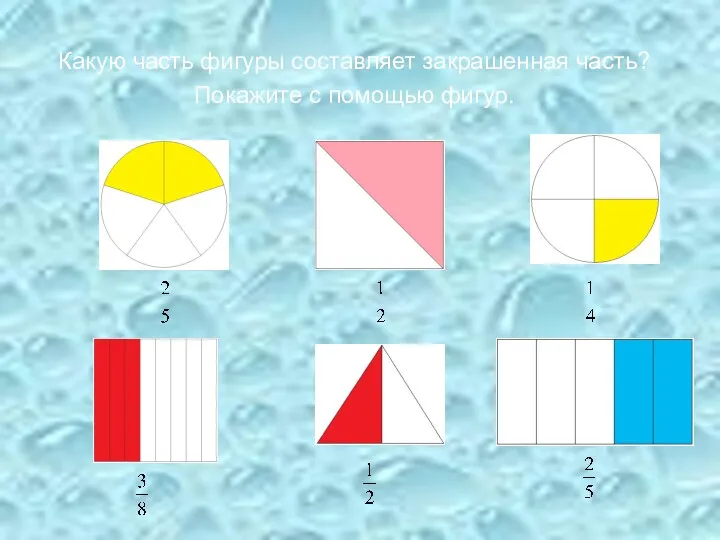 Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Остров “Решайка”. Остров “Мыслите
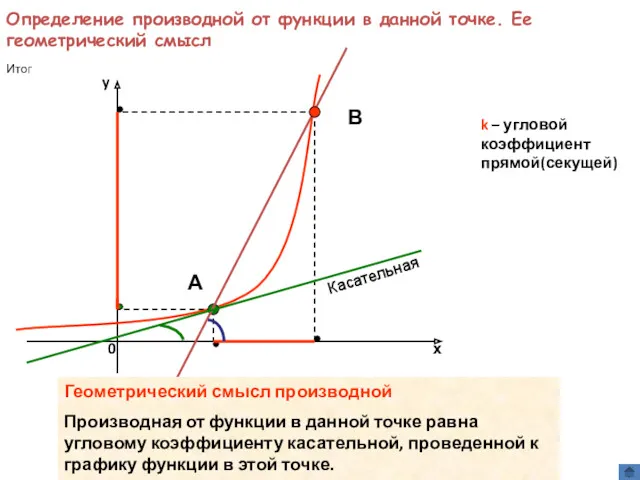
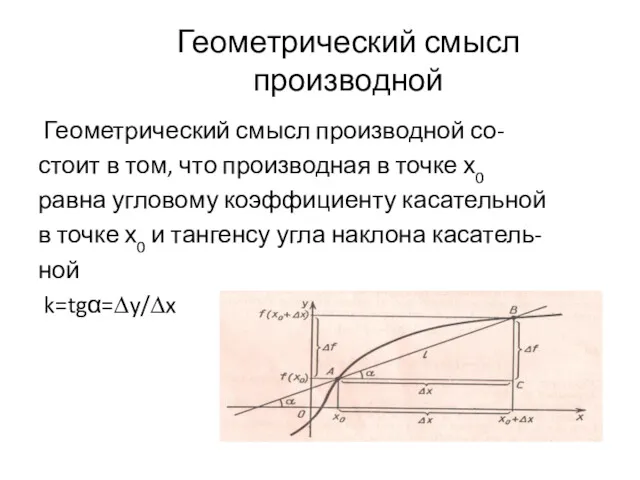
Остров “Решайка”. Остров “Мыслите Производная. Понятие производной. Производная частных функций
Производная. Понятие производной. Производная частных функций Многоугольники, вписанные в окружность. Геометрия, 8 класс
Многоугольники, вписанные в окружность. Геометрия, 8 класс Дисперсионный анализ
Дисперсионный анализ Делимость суммы и разности чисел. Урок 102
Делимость суммы и разности чисел. Урок 102 Свойство биссектрисы угла
Свойство биссектрисы угла ОГЭ по математике. Задание 1-5
ОГЭ по математике. Задание 1-5 Пропорциональность
Пропорциональность Множество действительных чисел
Множество действительных чисел Основы метрологии, стандартизации, сертификации и контроля качества
Основы метрологии, стандартизации, сертификации и контроля качества Графы. Вершина. Ребро. Представление задачи с помощью графов
Графы. Вершина. Ребро. Представление задачи с помощью графов Математический бой. 6 класс
Математический бой. 6 класс Розв’язання вправ. Квадратне рівняння
Розв’язання вправ. Квадратне рівняння Многоугольники
Многоугольники Исторические комбинаторные задачи. Различные комбинации трех элементов
Исторические комбинаторные задачи. Различные комбинации трех элементов Единицы длины. 5 класс
Единицы длины. 5 класс Что такое дробь?
Что такое дробь? Сравнение натуральных чисел. Математика 5 класс
Сравнение натуральных чисел. Математика 5 класс Математика на повторення (зимові канікули).
Математика на повторення (зимові канікули). Прямая пропорциональность. Актуализация опорных знаний
Прямая пропорциональность. Актуализация опорных знаний Решение задач и выражений
Решение задач и выражений Специфика возникновения нормального распределения применительно к объектам биологии и медицины
Специфика возникновения нормального распределения применительно к объектам биологии и медицины Диагностическая работа. Готовимся к ГИА. 9 класс
Диагностическая работа. Готовимся к ГИА. 9 класс Адаптивные фильтры. Практическое применение (2)
Адаптивные фильтры. Практическое применение (2) Числовые последовательности
Числовые последовательности