Содержание
- 2. Поверхности второго порядка Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют
- 3. 9) — эллиптический цилиндр, 10) — мнимый эллиптический цилиндр, 11) — две мнимые пересекающиеся плоскости (ось
- 4. Поверхность второго порядка, рассматриваемая как геометрический объект, не меняется, если от данной декартовой прямоугольной системы координат
- 5. Эллипсоид Каноническое уравнение эллипсоида имеет вид: Свойства эллипсоида: Эллипсоид обладает 1) Центральной симметрией относительно начала координат,
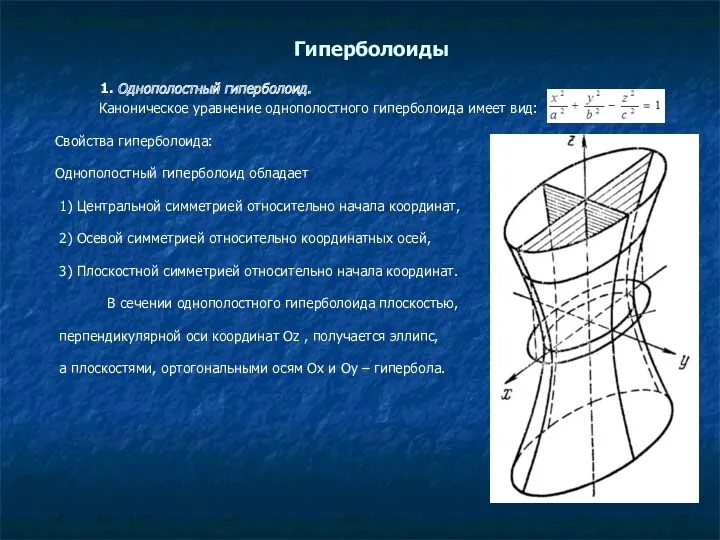
- 6. 1. Однополостный гиперболоид. Каноническое уравнение однополостного гиперболоида имеет вид: Свойства гиперболоида: Однополостный гиперболоид обладает 1) Центральной
- 7. 2. Двуполостный гиперболоид. Каноническое уравнение двуполостного гиперболоида имеет вид: Свойства двуполостного гиперболоида: Двуполостный гиперболоид обладает 1)
- 8. Параболоиды 1. Эллиптический параболоид. Каноническое уравнение эллиптического параболоида имеет вид: Свойства эллиптического параболоида: Эллиптический параболоид обладает
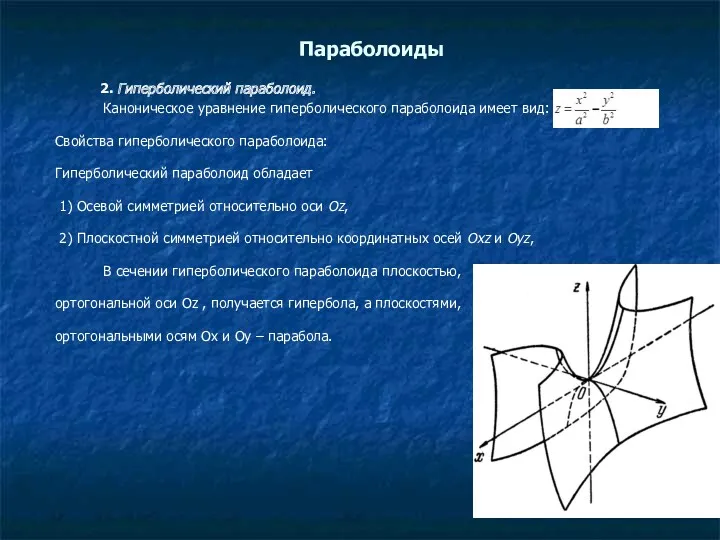
- 9. Параболоиды 2. Гиперболический параболоид. Каноническое уравнение гиперболического параболоида имеет вид: Свойства гиперболического параболоида: Гиперболический параболоид обладает
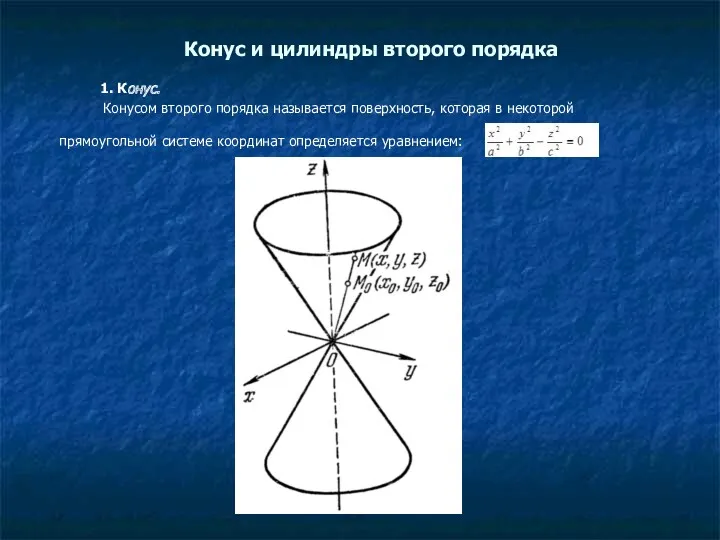
- 10. Конус и цилиндры второго порядка 1. Конус. Конусом второго порядка называется поверхность, которая в некоторой прямоугольной
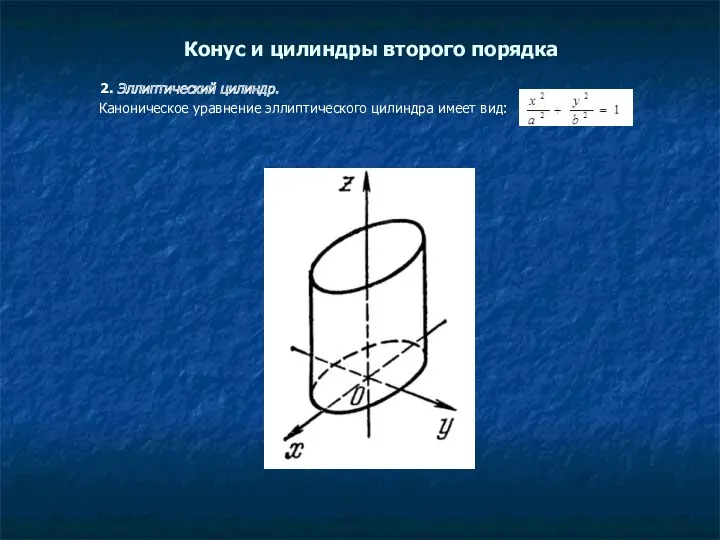
- 11. Конус и цилиндры второго порядка 2. Эллиптический цилиндр. Каноническое уравнение эллиптического цилиндра имеет вид:
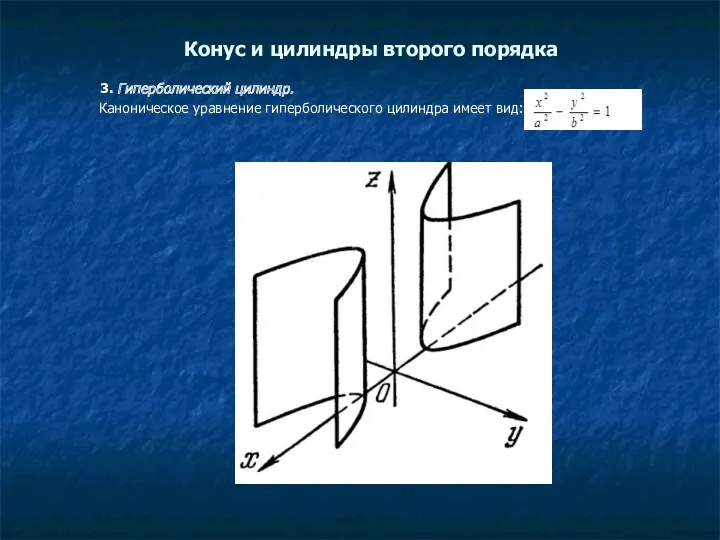
- 12. Конус и цилиндры второго порядка 3. Гиперболический цилиндр. Каноническое уравнение гиперболического цилиндра имеет вид:
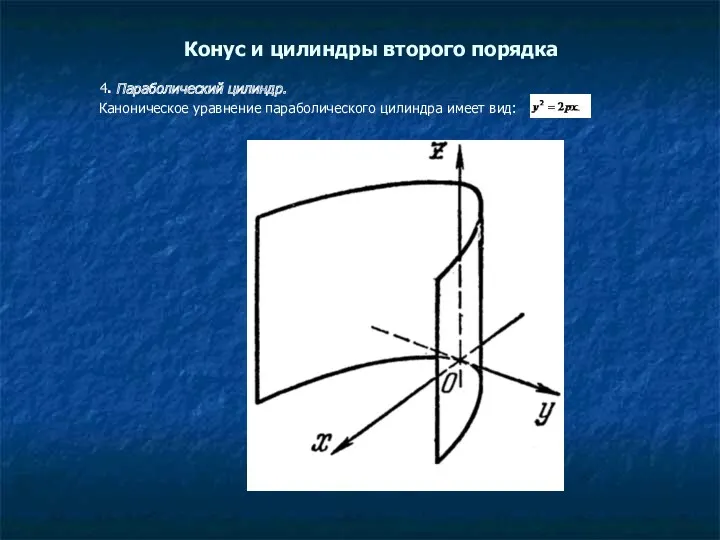
- 13. Конус и цилиндры второго порядка 4. Параболический цилиндр. Каноническое уравнение параболического цилиндра имеет вид:
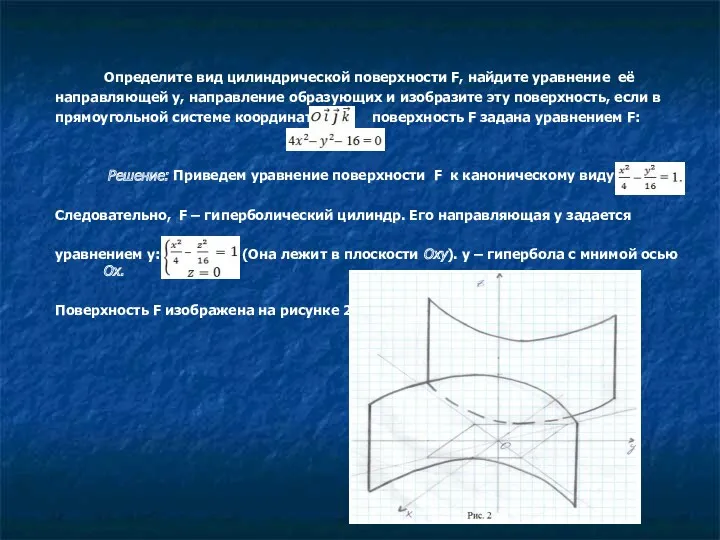
- 14. Задачи Определите вид цилиндрической поверхности F, найдите уравнение её направляющей y, направление образующих и изобразите эту
- 15. Определите вид цилиндрической поверхности F, найдите уравнение её направляющей y, направление образующих и изобразите эту поверхность,
- 17. Скачать презентацию







 Женщины - математики
Женщины - математики Прибавить и вычесть число 1.
Прибавить и вычесть число 1. Координатная плоскость
Координатная плоскость Зеркальная симметрия
Зеркальная симметрия Урок по математике в 3 классе
Урок по математике в 3 классе Линейная функция и её график
Линейная функция и её график Путешествие в страну математики
Путешествие в страну математики Урок – экскурсия. История космонавтики. Умножение десятичных дробей
Урок – экскурсия. История космонавтики. Умножение десятичных дробей 4 класс. Распределительное свойство умножения
4 класс. Распределительное свойство умножения Вимірювання параметрів історичних явищ і процесів
Вимірювання параметрів історичних явищ і процесів Сложение чисел с разными знаками
Сложение чисел с разными знаками Статистические характеристики
Статистические характеристики Квадратичная функция. Ее свойства и график. Проверка домашнего задания
Квадратичная функция. Ее свойства и график. Проверка домашнего задания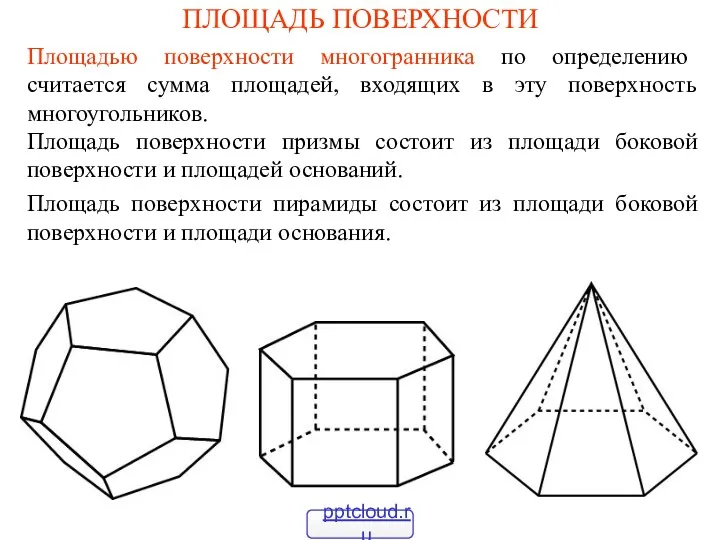 Площадь поверхности
Площадь поверхности Построение изометрической проекции окружности
Построение изометрической проекции окружности Методическая разработка урока - мастерской Что нам стоит дом построить по теме Площадь фигур
Методическая разработка урока - мастерской Что нам стоит дом построить по теме Площадь фигур Своя игра. 6 класс
Своя игра. 6 класс Комплексные числа
Комплексные числа Второй признак равенства треугольников
Второй признак равенства треугольников Первый признак равенства треугольников. 7 класс
Первый признак равенства треугольников. 7 класс Этапы расчета прогнозных значений методом прогнозной экспраполяции
Этапы расчета прогнозных значений методом прогнозной экспраполяции Основные сведения из теории вероятностей. Лекция 1
Основные сведения из теории вероятностей. Лекция 1 Общий приём вычитания
Общий приём вычитания Измерение и количественный анализ данных. Описательная статистика
Измерение и количественный анализ данных. Описательная статистика Биостатистика. Сапалы белгілерді талдау
Биостатистика. Сапалы белгілерді талдау Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Геометриялық пішіндер. Дидактикалық ойындар
Геометриялық пішіндер. Дидактикалық ойындар Інтелектуальна гра Найрозумніший з математики
Інтелектуальна гра Найрозумніший з математики