Содержание
- 2. Определение 1. Функцию вида у= f (х), х ϵ Ν называют функцией натурального аргумента или числовой
- 3. Словесный способ. Правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности
- 4. 2. Аналитический способ. Любой n-й элемент последовательности можно определить с помощью формулы. Способы задания числовой последовательности
- 5. 3. Рекуррентный способ. Указывается правило, позволяющее вычислить n-й элемент последовательности, если известен ее предыдущий элемент. Способы
- 6. Продолжите ряд: 1, 10, 3, 9, 5, 8, 7, 7, 9, 6… Продолжите ряд 77, 49,
- 7. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610… Числа
- 8. Определение 2. Последовательность (уn), называют ограниченной сверху, если все ее члены не больше некоторого числа. Последовательность
- 9. Определение 3. Последовательность (уn), называют ограниченной снизу, если все ее члены не меньше некоторого числа. Последовательность
- 10. Если последовательность ограничена и снизу и сверху, то ее называют ограниченной последовательностью. Ограниченность последовательности означает, что
- 11. Члены последовательности (уn) как бы «сгущаются» около точки 0. Говорят последовательность (уn) сходится. У последовательности (уn)
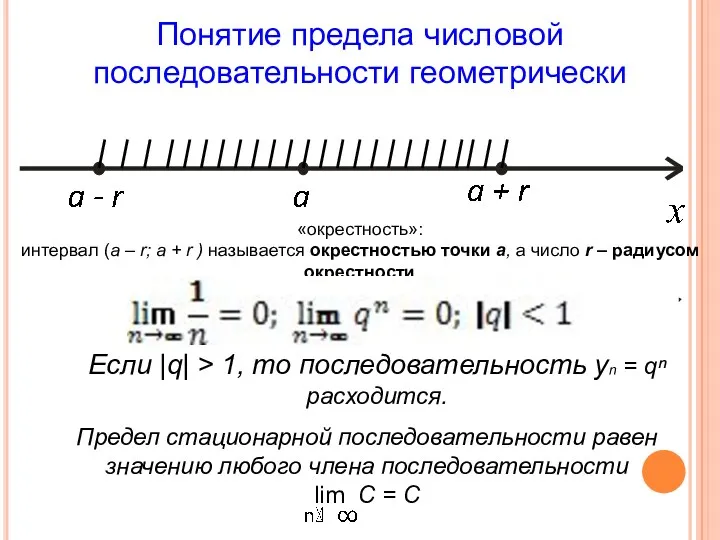
- 12. Определение 6. Число b называют пределом последовательности (уn), если в любой заранее выбранной окрестности точки b
- 13. Понятие предела числовой последовательности геометрически «окрестность»: интервал (а – r; а + r ) называется окрестностью
- 14. Свойства сходящихся последовательностей. Свойство 1. Если последовательность сходится, то только к одному пределу. Свойство 2. Если
- 15. «ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ». Теорема Если lim xn = b, lim yn = c ,то предел
- 17. Скачать презентацию













 Урок математики 3классСложение и вычитание трехзначных чисел
Урок математики 3классСложение и вычитание трехзначных чисел Линейные векторные пространства. Базис
Линейные векторные пространства. Базис Методы прогнозирования динамики экономических процессов
Методы прогнозирования динамики экономических процессов Математические сказки
Математические сказки Презентация к уроку по математике на тему Сложение и вычитание величин по УМК Перспективная начальная школа
Презентация к уроку по математике на тему Сложение и вычитание величин по УМК Перспективная начальная школа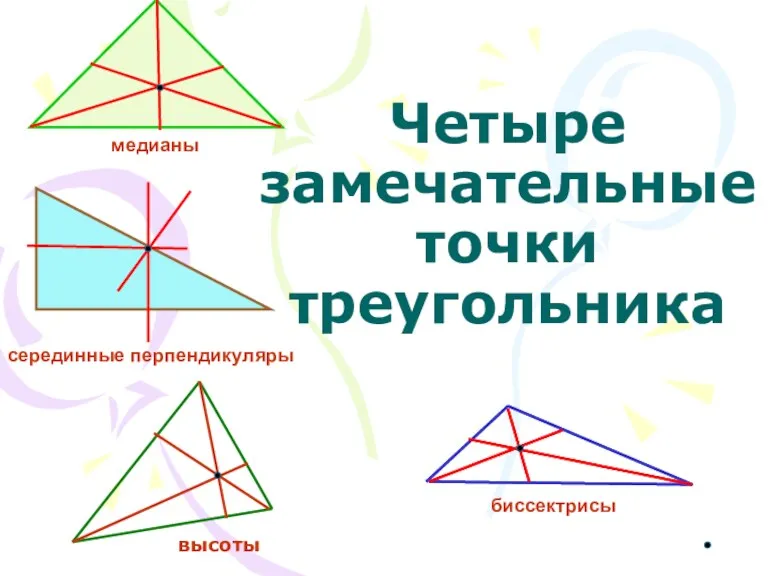 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Сравнение трёхзначных чисел. 3 класс
Сравнение трёхзначных чисел. 3 класс Перпендикуляр и наклонные к плоскости
Перпендикуляр и наклонные к плоскости Нумерация в концентре 1000
Нумерация в концентре 1000 Умножение десятичных дробей
Умножение десятичных дробей Прибавление и вычитание числа 4 Математика 1 класс
Прибавление и вычитание числа 4 Математика 1 класс Точка. Прямая. Отрезок
Точка. Прямая. Отрезок Сумма углов треугольника. Задания для устного счета. Упражнение 9. 7 класс
Сумма углов треугольника. Задания для устного счета. Упражнение 9. 7 класс Геометрические преобразования в пространстве
Геометрические преобразования в пространстве Симметрия
Симметрия Причинно-следственная диаграмма Исикавы
Причинно-следственная диаграмма Исикавы Экстремум функции двух переменных
Экстремум функции двух переменных Презентация Прямая (геометрический материал)
Презентация Прямая (геометрический материал) Геометрический и физический смысл приращения аргумента и приращения функции (для ВК)
Геометрический и физический смысл приращения аргумента и приращения функции (для ВК) Игры на развитие математических способностей детей младшего дошкольного возраста.
Игры на развитие математических способностей детей младшего дошкольного возраста. Презентация к уроку математики в 1 классе Сложение и вычитание в пределах 20
Презентация к уроку математики в 1 классе Сложение и вычитание в пределах 20 Первообразная. Неопределенный интеграл
Первообразная. Неопределенный интеграл Стереометрия. Пирамида
Стереометрия. Пирамида Численные методы алгебры
Численные методы алгебры Сумма углов треугольника
Сумма углов треугольника Трудные случаи таблицы умножения и деления
Трудные случаи таблицы умножения и деления Симметрия правильных многогранников
Симметрия правильных многогранников Единицы измерения. Тонна. Центнер.
Единицы измерения. Тонна. Центнер.