Содержание
- 2. ПРАВИЛО ЛОПИТАЛЯ Теорема Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их
- 3. То есть если существует неопределенность вида то
- 4. ПРИМЕРЫ Вычислить пределы, используя правило Лопиталя: 1
- 5. Решение:
- 6. 2
- 7. Решение:
- 8. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ ТЕОРЕМА 1 (достаточное условие возрастания функции)
- 9. Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.
- 10. ТЕОРЕМА 2 (достаточное условие убывания функции) Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то
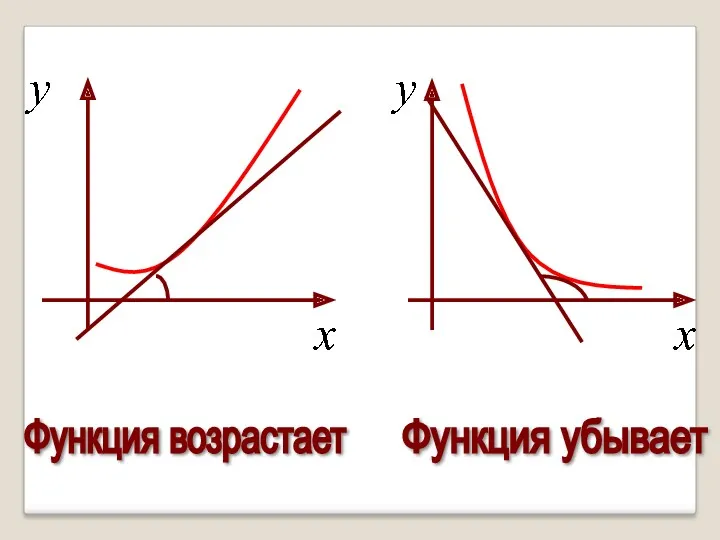
- 11. Геометрическая интерпретация Если касательные к кривой на некотором промежутке направлены под острыми углами к оси х,
- 12. Функция возрастает Функция убывает
- 13. Пример Найти интервалы монотонности функции
- 14. Решение: Найдем производную этой функции: Исследуем знак этой производной:
- 15. Следовательно, функция будет возрастать на промежутке Функция будет убывать на промежутке
- 16. ЭКСТРЕМУМ ФУНКЦИИ Точка х0 называется точкой максимума функции f(x), если в некоторой окрестности точки х0 выполняется
- 17. Точка х1 называется точкой минимума функции f(x), если в некоторой окрестности точки х1 выполняется неравенство
- 18. Значения функции в точках х0 и х1 называются соответственно точками максимума и минимума. Максимум и минимум
- 19. max min max
- 20. Если в некоторой точке х0 дифференцируемая функция f(x) имеет экстремум, то в некоторой окрестности этой точки
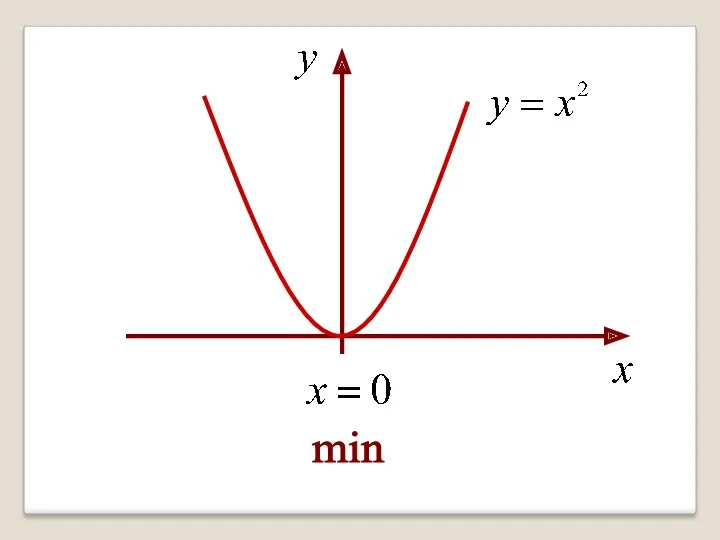
- 21. Однако, функция может иметь экстремум в точке, в которой она не дифференцируема. Например, функция имеет минимум
- 22. Необходимое условие экстремума Для того, чтобы функция y=f(x) имела экстремум в точке х0 , необходимо, чтобы
- 23. Точки, в которых выполняется необходимое условие экстремума, называются критическими или стационарными. Если в какой-либо точке имеется
- 24. Примеры Найти критические точки и экстремумы функций: 1
- 25. Решение: Применим необходимое условие экстремума: - критическая точка
- 26. min
- 27. 2
- 28. Решение: Применим необходимое условие экстремума: - критическая точка
- 30. Первое достаточное условие экстремума Если при переходе через точку х0 производная дифференцируемой функции y=f(x) меняет знак
- 31. Схема исследования функции на экстремум 1 Найти производную функции
- 32. 2 Найти критические точки функции, в которых производная равна нулю или не существует.
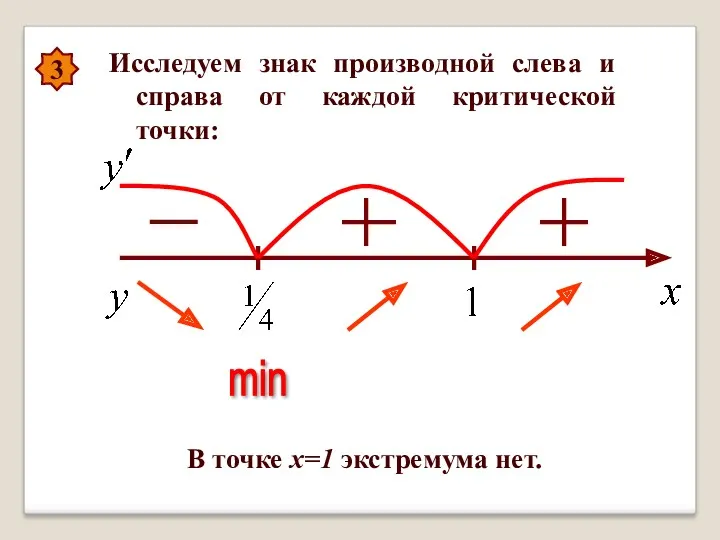
- 33. 3 Исследовать знак производной слева и справа от каждой критической точки.
- 34. 4 Найти экстремум функции.
- 35. Пример Исследовать функцию на экстремум:
- 36. Решение: Применим схему исследования функции на экстремум: 1 Находим производную функции:
- 37. 2 Находим критические точки: критические точки
- 38. 3 Исследуем знак производной слева и справа от каждой критической точки: min В точке х=1 экстремума
- 39. 4 Находим экстремум функции:
- 40. Второе достаточное условие экстремума Если первая производная дифференцируемой функции y=f(x) в точке х0 равна нулю, а
- 41. Схема исследования функции на экстремум в этом случае аналогична предыдущей, но третий пункт следует заменить на:
- 42. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ Согласно теореме Вейерштрасса, если функция непрерывна на отрезке [a;b],
- 43. Схема нахождения наибольшего и наименьшего значения функции на отрезке 1 Найти производную функции.
- 44. 2 Найти критические точки, в которых производная равна нулю или не существует. 3 Найти значения функции
- 45. пример Найти наибольшее и наименьшее значения функции на отрезке
- 46. решение: 1 Находим производную функции: 2 Находим критические точки: критические точки
- 47. 3 Находим значения функций в критических точках и на концах отрезка:
- 49. Скачать презентацию





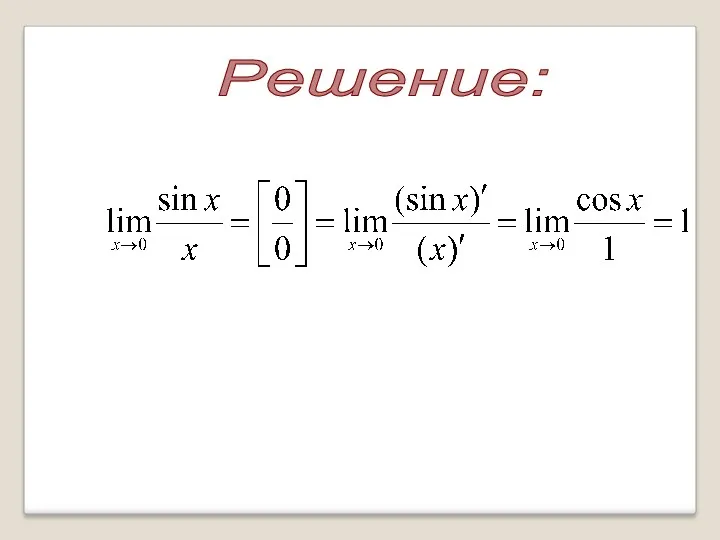





































 Вероятность равновозможных событий
Вероятность равновозможных событий Деление с остатком. 5 класс
Деление с остатком. 5 класс Математические фокусы. Виды фокусов
Математические фокусы. Виды фокусов Тригонометрический круг
Тригонометрический круг Урок математики Внетабличное деление вида 87 : 29 3 класс
Урок математики Внетабличное деление вида 87 : 29 3 класс Классическое определение вероятности
Классическое определение вероятности Методы построения графиков функций с использованием свойств функции
Методы построения графиков функций с использованием свойств функции Действительные числа
Действительные числа Умники и умницы. Матиматека
Умники и умницы. Матиматека Презентация Закрепление таблицы умножения
Презентация Закрепление таблицы умножения Презентация к уроку математики по теме Признаки предметов 1 класс, программа 2100, урок №5
Презентация к уроку математики по теме Признаки предметов 1 класс, программа 2100, урок №5 Производная
Производная Восемь способов решения одного тригонометрического уравнения
Восемь способов решения одного тригонометрического уравнения Занимательная математика
Занимательная математика Понятие отношения
Понятие отношения Презентация для интерактивной доски
Презентация для интерактивной доски Trigonometry 1
Trigonometry 1 Деление с остатком
Деление с остатком Правила построения рядов динамики
Правила построения рядов динамики Площади фигур. Теорема Пифагора
Площади фигур. Теорема Пифагора Функция. Свойства функции
Функция. Свойства функции Десятичная запись дробных чисел
Десятичная запись дробных чисел Прямая, луч, отрезок.Выполнена учителем начальных классов Поповой Т.Д. Скачать бесплатно и без регистрации
Прямая, луч, отрезок.Выполнена учителем начальных классов Поповой Т.Д. Скачать бесплатно и без регистрации Сфера и шар. Теорема
Сфера и шар. Теорема Трапеция. 8 класс
Трапеция. 8 класс Решение уравнений. Урок математики
Решение уравнений. Урок математики Число 7, цифра 7.
Число 7, цифра 7. Нахождение числа по заданному значению его дроби
Нахождение числа по заданному значению его дроби