Статистическая оценка параметров распределений презентация

План лекции:
Свойства выборочных характеристик.
Точечная оценка параметров распределения. Метод моментов.
Метод максимального правдоподобия.
Основные статистические распределения. Распределение χ2.
Распределение Стьюдента.
Распределение Фишера –Снедекора.

Актуальность темы
Вычисление статистических оценок параметров распределений является одной из наиболее важных задач математической статистики

Пусть плотность распределения элементов выборки является непрерывной функцией. Если количество интервалов группировки стремится к бесконечности таким образом, что (k/n)→0, то имеет место сходимость по вероятности гистограммы к плотности в каждой точке y.
Сходимость эмпирических характеристик к теоретическим

Статистическая функция распределения
При увеличении числа опытов n, согласно теореме Бернулли, при любом x частота события X

Теорема Гливенко-Кантелли
Верен и более общий результат, показывающий, что сходимость эмпирической функции распределения к теоретической имеет равномерный характер
Если F - непрерывна, то скорость сходимости к нулю имеет порядок

Свойства выборочных характеристик
Пусть есть выборка наблюдений случайной величины X - {х1,…,хn} и пусть Θn(х1,…,хn) есть статистика, оценка неизвестного параметра Θ, зависящая от наблюдений выборки: Θ ≈ Θn.
(Θn-случайная величина, меняющаяся
от выборки к выборке).
Для правильной аппроксимации параметра генеральной совокупности Θ выборочная оценка Θn по правилам математической статистики должна быть состоятельной, эффективной и несмещенной.

Свойства выборочных характеристик
Оценка Θn(х1,…,хn) называется состоятельной оценкой параметра Θ, если она сходится по вероятности к оцениваемому параметру Θ при n→∞.
то есть вероятность отклонения оценки от истинного значения параметра можно сделать сколь угодно малой, увеличивая объем выборки.
Если α0 – точное значение параметра генеральной совокупности, α – точечная оценка этого параметра, то требование состоятельности оценки математически записывается в виде:

Свойства выборочных характеристик
Оценка Θn называется несмещенной оценкой параметра Θ, если при любом n:
М(Θn) = Θ или Mα = α0
Это означает, что отклонение Θn от Θ не содержит систематической ошибки.
В противном случае оценка называется смещенной.
Величина М(Θn(х1,…,хn) – Θ) называется смещением оценки Θ.

Эффективной называют статистическую оценку, которая при заданном объеме выборки n имеет наименьшую дисперсию.
Dα → min
т.о. для того, чтобы оценка Θn(х1,…,хn) была состоятельной оценкой неизвестного параметра Θ достаточно, чтобы ее математическое ожидание стремилось к Θ, а дисперсия стремилось к нулю при n→∞.

Свойства выборочных характеристик
Оценка Θn(х1,…,хn) называется
асимптотически несмещенной,
если ее смещение
(МΘn(х1,…,хn) – Θ) →0 при n→∞.
Оценка Θn(х1,…,хn) называется
сходящейся в среднеквадратическом к оцениваемому параметру Θ,
если М(Θn(х1,…,хn) – Θ)2→0 при n→∞.
(из сходимости в среднеквадратическом следует сходимость по вероятности).
Несмещенные оценки не всегда дают хорошее приближение для оцениваемого параметра. Например, наблюдаемая по одной выборке Θ1 оценка может быть сильно удалено от среднего значения выборки, а следовательно, и от оцениваемого параметра.

Свойства выборочных моментов
Выборочное среднее является несмещенной, сходится в среднеквадратическом (следовательно является состоятельной) и асимптотически нормальной оценкой для теоретического среднего (математического ожидания).
Выборочные дисперсии σ2 и s2 являются состоятельными оценками для истинной дисперсии:
Величина σ2 - смещенная, а s2 - несмещенная оценка дисперсии D(X)

Смещенная выборочная дисперсия (n<30):
Математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии
Несмещенная (исправленная) оценка дисперсии D(X)

Выборочные начальные моменты С.В. Х являются состоятельными и несмещенными оценками соответствующих начальных моментов.
Выборочные центральные моменты С.В. Х являются состоятельными но смещенными оценками.
(Величина смещения ≈1/n при n→∞)

Методы оценки точечных параметров распределения
Точечная оценка предполагает нахождение единственной числовой величины, которая и принимается за значение параметра.
Такую оценку целесообразно определять в тех случаях, когда объем выборки достаточно велик. Причем не существует единого понятия о достаточном объеме выборки, его значение зависит от вида оцениваемого параметра, а предварительно будем считать достаточной выборку, содержащую не менее чем 10 значений). При малом объеме выборки точечные оценки могут значительно отличаться от истинных значений параметров, что делает их непригодными для использования.

Задача точечной оценки параметров в типовом варианте постановки состоит в следующем:
Имеется: выборка наблюдений (x1, x2, …, xn) за случайной величиной Х. Объем выборки n фиксирован.
Известен вид закона распределения величины Х, например, в форме плотности распределения f(x, Θ), где Θ – неизвестный (в общем случае векторный) параметр распределения. Параметр Θ является неслучайной величиной.
Требуется найти оценку Θn параметра Θ закона распределения.

Существует несколько методов решения задачи точечной оценки параметров, наиболее часто применяются методы моментов и максимального (наибольшего) правдоподобия

Метод моментов для точечной оценки параметров распределения
Состоит в приравнивании теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же порядка (К. Пирсон, 1894 г. )
Оценка одного параметра
Пусть задан вид плотности распределения вероятности f(x, Θ), определяемый одним неизвестным параметром Θ.
-уравнение с одним неизвестным Θ. Решив его, найдем точечную оценку Θn, которая является функцией от выборочной средней, следовательно, и от вариант выборки:
Θn=ψ(х1,…,хn)

Пример:
Найти методом моментов по выборке (х1,…,хn) точечную оценку неизвестного параметра λ показательного распределения:
f(x)= λe- λx (x≥0)
Решение: Приравниваем начальный теоретический момент 1 порядка эмпирическому начальному моменту 1 порядка:
Отсюда
Точечная оценка параметра λ показательного распределения равна величине, обратной выборочной средней

Пример:
Проведено четыре измерения некоторой случайной величины (в мм): 3; 4; 5; 8. Найти методом моментов точечную оценку неизвестного параметра λ. Записать функции f(x) и F(x).
Решение:
λ=1/5=0,2 f(x)= 0,2e- 0,2x F(x)=1- e- 0,2x

Оценка двух параметров
Задана функция плотности распределения, определяемая двумя неизвестными параметрами f(x, Θ1, Θ2). Необходимо составить два уравнения относительно этих параметров. Приравняем начальный теоретический момент 1 порядка эмпирическому начальному моменту 1 порядка и центральный теоретический момент 2 порядка центральному эмпирическому моменту 2 порядка:
α1=M(x) μ2=m2=D(x)

M(x) и D(X) – функции от Θ1, Θ2. Поэтому получили систему с двумя неизвестными. Решив эту систему получим точечные оценки Θ1т, Θ2т, являющиеся функциями вариант выборки:
Θ1n=ψ1(х1,…,хn)
Θ2n=ψ2(х1,…,хn)

Пример:
Найти методом моментов по выборке (х1,…,хn) точечную оценку неизвестных параметров a и σ нормального распределения:
Точечные оценки параметров нормального распределения:

Метод моментов позволяет получить состоятельные оценки, они при довольно общих условиях распределены асимптотически нормально. Смещение удается устранить введением поправок. Эффективность оценок невысокая, т.е. даже при больших объемах выборок дисперсия оценок относительно велика (за исключением нормального распределения, для которого метод моментов дает эффективные оценки).
Метод целесообразно применять для оценки не более чем четырех параметров, так как точность выборочных моментов резко падает с увеличением их порядка.

Метод максимального правдоподобия
(Р. Фишер, 1912 г.)
Состоит в том, что в качестве «наиболее правдоподобного» значения параметра берут значение Θ, максимизирующее вероятность получить при n опытах данную выборку (х1,…,хn)
Нахождение оценок максимального правдоподобия включает следующие этапы:
построение функции правдоподобия (ее натурального логарифма);
дифференцирование функции по искомым параметрам и составление системы уравнений;
решение системы уравнений для нахождения оценок;
определение второй производной функции, проверку ее знака в точке оптимума первой производной, нахождение максимума;
формирование выводов.

Метод максимального правдоподобия
Пусть Х - С.В., которая в результате n испытаний приняла значения (х1 ,…, хn).
Вид закона распределения Х задан, но неизвестен параметр Θ, которым определяется этот закон. Требуется найти его точечную оценку.
Обозначим вероятность того, что в результате опыта Х примет значение xi (i=1, 2, 3,…,n) p(xi; Θ).
Функцией правдоподобия ДСВ Х называют функцию аргумента Θ:
L(х1 ,…, хn ; Θ)= p(x1; Θ) ⋅ p(x2; Θ) ⋅ … ⋅ p(xn; Θ),
где (х1 ,…, хn) - фиксированные числа.

Метод максимального правдоподобия
Функцией правдоподобия НСВ Х называют совместную плотность вероятности
L(х1, х2 …, хn ; Θ) = f(х1, Θ)⋅f(х2, Θ) ⋅ … ⋅ f(хn, Θ)
В качестве точечной оценки параметра Θ принимают такое его значение Θn, при котором функция правдоподобия достигает максимума.
Оценку Θn-называют оценкой максимального правдоподобия.

Функции L и ln L достигают максимума при одном и том же значении Θ. Удобнее пользоваться ln L – логарифмической функцией правдоподобия.
Нахождение максимума функции:
Найти производную
Приравнять производную к 0, найти корень полученного уравнения (критическую точку)
Найти вторую производную . Если вторая производная при Θ= Θn отрицательна, то Θn – точка максимума.

Пример:
Найти методом наибольшего правдоподобия оценку параметра λ распределения Пуассона:
mi-число произведенных испытаний, хi-число появления события в i-ом опыте (i=1,2,…,n). Опыт состоит из m испытаний.
Решение: θ= λ. Составим функцию правдоподобия: L=p(x1; λ)⋅ p(x2;;λ) ⋅, …, ⋅ p(xn; λ)=
=

Найдем логарифмическую функцию правдоподобия:
Ln L=(Σxi)⋅lnλ - n λ - ln(x1!x2!...xn!)
Найдем первую производную по λ:
Запишем уравнение правдоподобия, приравняв первую производную 0:
(Σxi/ λ) - n=0
Найдем критическую точку:
λ = (Σxi/n) =
Найдем вторую производную по λ:

При λ = вторая производная отрицательна, следовательно λ-точка максимума. В качестве оценки наибольшего правдоподобия параметра λ распределения Пуассона нужно принять выборочную среднюю:
λ*=

Достоинства метода:
Оценки наибольшего правдоподобия состоятельны (м.б. смещенными), распределены асимптотически нормально (при больших n приближенно нормальны) и имеют наименьшую дисперсию. Этот метод наиболее полно использует данные выборки, особенно полезен при малых выборках.
Недостаток – сложные вычисления.

Основные статистические
распределения, связанные
с нормальным распределением

Распределение хи-квадрат (χ2)
Пусть Хi (i=1,2,…,n)-нормальные независимые СВ, причем математическое ожидание каждой из них равно 0, а среднее квадратическое отклонение равно 1. Тогда сумма квадратов этих величин:
Распределена по закону хи-квадрат с k=n степенями свободы. Если эти величины связаны линейным соотношением, например:
то k=n-1

Плотность распределения:
где гамма функция Эйлера, х = χ2
например: Г(n+1)=n!
Распределение «хи-квадрат» определяется одним параметром - числом степеней свободы k. При увеличении числа степеней свободы распределение медленно приближается к нормальному.

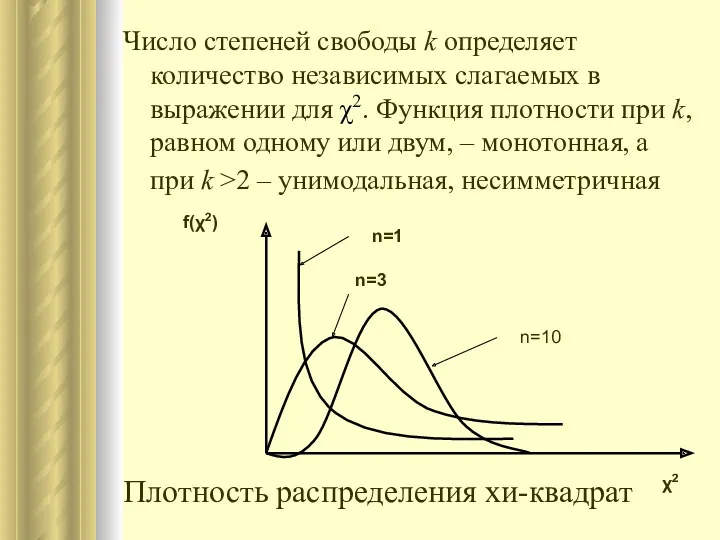
Число степеней свободы k определяет количество независимых слагаемых в выражении для χ2. Функция плотности при k, равном одному или двум, – монотонная, а при k >2 – унимодальная, несимметричная
Плотность распределения хи-квадрат
χ2

Математическое ожидание и дисперсия величины χ2 равны соответственно k и 2k. Распределение хи-квадрат является частным случаем более общего гамма-распределения, а величина, равная корню квадратному из хи-квадрат с двумя степенями свободы, подчиняется распределению Рэлея.

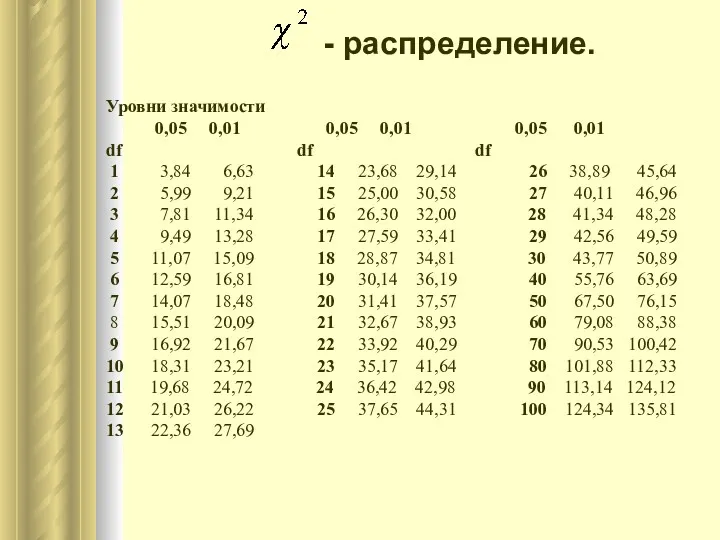
Уровни значимости
0,05 0,01 0,05 0,01 0,05 0,01
df df df 1 3,84 6,63 14 23,68 29,14 26 38,89 45,64
2 5,99 9,21 15 25,00 30,58 27 40,11 46,96
3 7,81 11,34 16 26,30 32,00 28 41,34 48,28
4 9,49 13,28 17 27,59 33,41 29 42,56 49,59
5 11,07 15,09 18 28,87 34,81 30 43,77 50,89
6 12,59 16,81 19 30,14 36,19 40 55,76 63,69
7 14,07 18,48 20 31,41 37,57 50 67,50 76,15
8 15,51 20,09 21 32,67 38,93 60 79,08 88,38
9 16,92 21,67 22 33,92 40,29 70 90,53 100,42
10 18,31 23,21 23 35,17 41,64 80 101,88 112,33
11 19,68 24,72 24 36,42 42,98 90 113,14 124,12
12 21,03 26,22 25 37,65 44,31 100 124,34 135,81
13 22,36 27,69
- распределение.

Распределение Стьюдента
t-распределение, предложено в 1908 г. английским статистиком В. Госсетом, публиковавшим научные труды под псевдонимом Student
Пусть X, X1 , X2 … Xk –нормальные независимые СВ, причем математическое ожидание каждой из них равно 0, а среднее квадратическое отклонение равно 1. Тогда величина:
имеет t-распределение Стьюдента с k степенями свободы

Дифференциальная функция распределения Стьюдента:
Распределение не зависит от σ в силу безразмерности t. Распределение Стьюдента быстрее, чем χ2 сходится к нормальному. Величина k характеризует количество степеней свободы.
Плотность распределения – унимодальная и симметричная функция, похожая на нормальное распределение

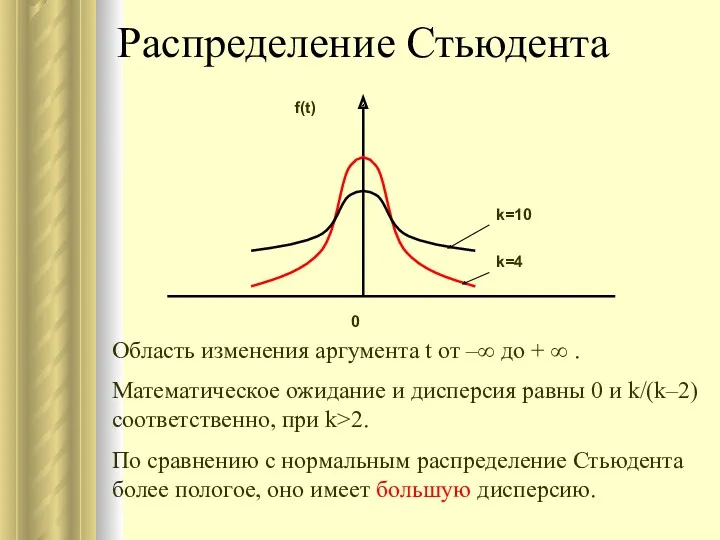
Распределение Стьюдента
Область изменения аргумента t от –∞ до + ∞ .
Математическое ожидание и дисперсия равны 0 и k/(k–2) соответственно, при k>2.
По сравнению с нормальным распределение Стьюдента более пологое, оно имеет большую дисперсию.

Коэффициент нормированных отклонений Стьюдента

Распределение Фишера (Фишера –Снедекора)
Пусть X1 , X2 … Xm и Y1 , Y2 … Yn –одинаково распределенные по нормальному закону взаимно независимые СВ, для которых математическое ожидание равно 0, а среднее квадратическое отклонение равно 1. Тогда величина:
имеет распределение Фишера (F-распределение) с k1=m - числом степеней свободы числителя и k2=n - числом степеней свободы знаменателя.

Плотность распределения:
Область изменения аргумента х от 0 до ∞ .
В этом выражении k1 обозначает число степеней свободы величины Х с большей дисперсией, k2 – число степеней свободы величины Y с меньшей дисперсией. Плотность распределения – унимодальная, несимметричная.

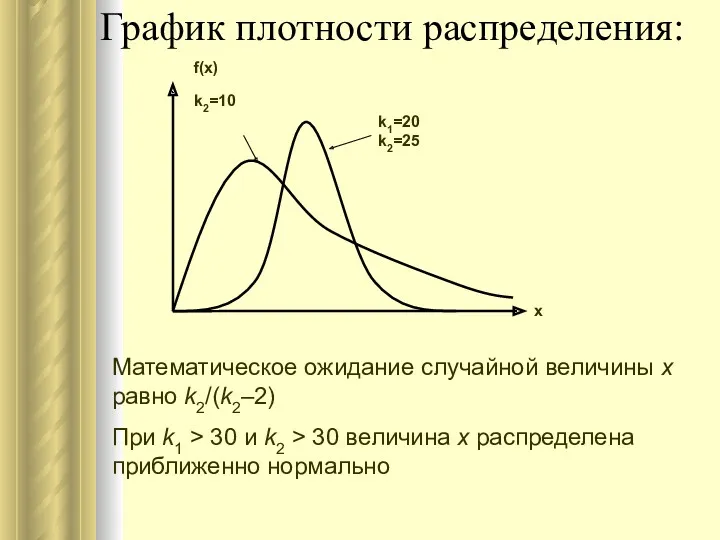
График плотности распределения:
Математическое ожидание случайной величины х равно k2/(k2–2)
При k1 > 30 и k2 > 30 величина х распределена приближенно нормально

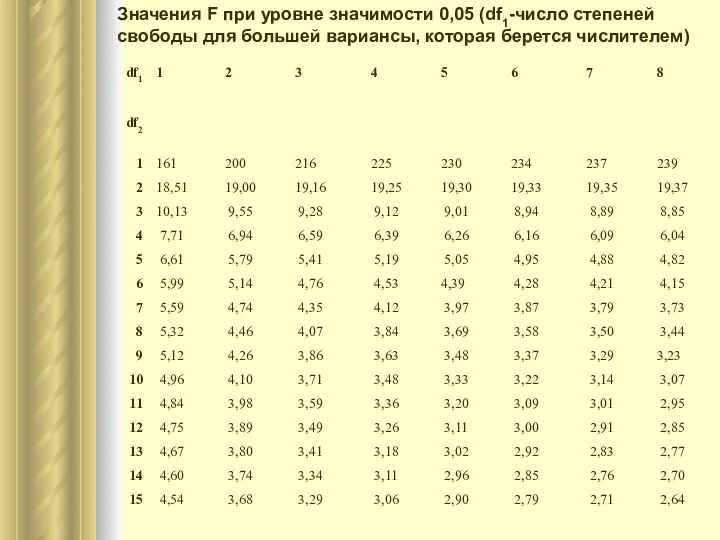
Значения F при уровне значимости 0,05 (df1-число степеней свободы для большей вариансы, которая берется числителем)

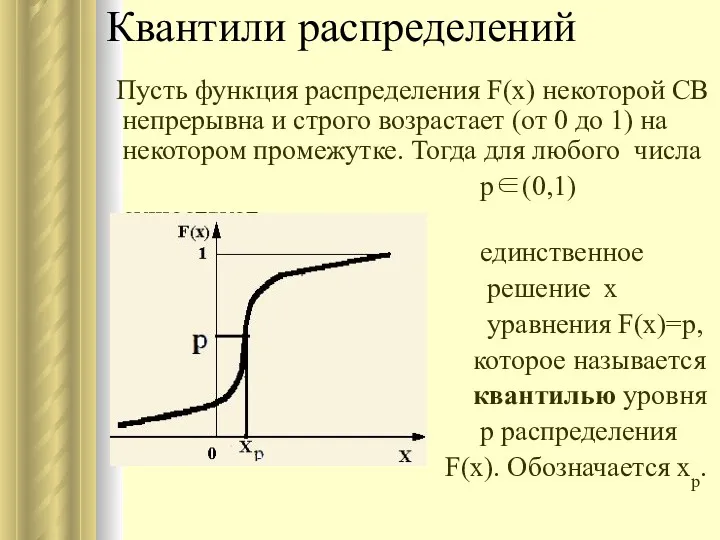
Квантили распределений
Пусть функция распределения F(x) некоторой СВ непрерывна и строго возрастает (от 0 до 1) на некотором промежутке. Тогда для любого числа
p∈(0,1) существует
единственное
решение х
уравнения F(x)=p,
которое называется
квантилью уровня
р распределения
F(x). Обозначается хр.

FРАСПОБР(вероятность;степени_свободы1;степени_свободы2)
Вероятность — это вероятность, связанная с F-распределением.
Степени_свободы1 — это числитель степеней свободы.
Степени_свободы2 — это знаменатель степеней свободы.
СТЬЮДРАСПОБР(вероятность;степени_свободы)
Вероятность — вероятность, соответствующая двустороннему распределению Стьюдента.
Степени_свободы — число степеней свободы, характеризующее распределение.
ХИ2ОБР(вероятность;степени_свободы)
Вероятность — это вероятность, связанная с распределением χ2 (хи-квадрат).
Степени свободы — это число степеней свободы.

Заключение
Нами рассмотрены:
Статистические оценки параметров распределения;
Свойства выборочных характеристик;
Методы нахождения точечных оценок параметров распределения.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:
Основная литература:
Попов А.М. Теория вероятней и математическая статистика /А.М. Попов, В.Н. Сотников. – М.: ЮРАЙТ, 2011. – 440 с.
Гмурман В. Е. Теория вероятностей и математическая статистика: учебное пособие / В.Е. Гмурман. – М. : Высш. шк., 2011. – 479с.
Балдин К. В. Основы теории вероятностей и математической статистики : учебник / К. В. Балдин. – М. : Флинта, 2010. – 488с.
Учебно–методические пособия:
Шапиро Л.А., Шилина Н.Г. Руководство к практическим занятиям по медицинской и биологической статистике Красноярск: ООО «Поликом». – 2003.