Содержание
- 2. МЕТОД ПРОСТОЇ ІТЕРАЦІЇ Припустимо, що і перетворимо систему до вигляду
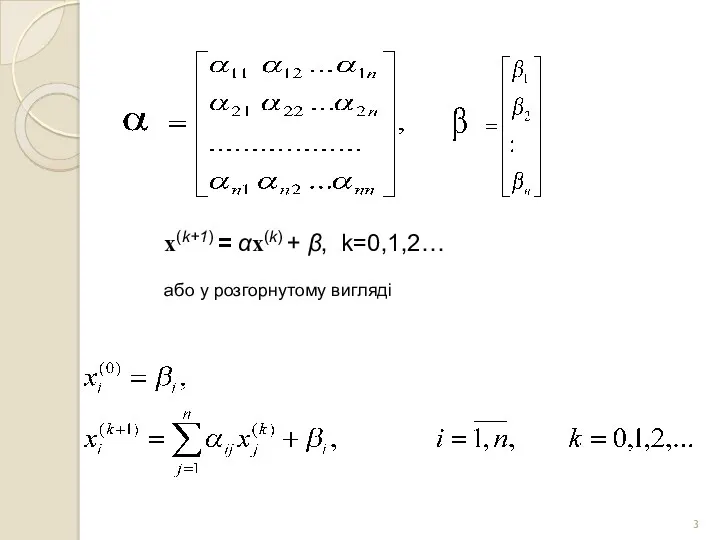
- 3. x(k+1) = αx(k) + β, k=0,1,2… або у розгорнутому вигляді
- 7. ЗБІЖНІСТЬ МЕТОДУ ПРОСТОЇ ІТЕРАЦІЇ Для збіжності процесу обчислень необхідно, щоб виконувалась умова ||α|| Відповідно для різних
- 8. Теорема Якщо матриця α системи рівнянь x(k+1) = αx(k) + β задовольняє одну із умов то
- 9. ПОХИБКИ МЕТОДУ ПРОСТОЇ ІТЕРАЦІЇ Глобальна похибка розв’язку на двох сусідніх ітераціях ||x(k+1) – x*|| = ||α||
- 10. МЕТОД ЯКОБІ Запишемо метод Якобі в матричній формі. Для цього запишемо матрицю A як: A =
- 11. МЕТОД ЯКОБІ Запишемо СЛАР як: (L + D + U)x = b або Dx = b
- 12. МЕТОД ЯКОБІ При цьому Для збіжності методу Якобі достатньо, щоб матриця α мала домінуючу головну діагональ:
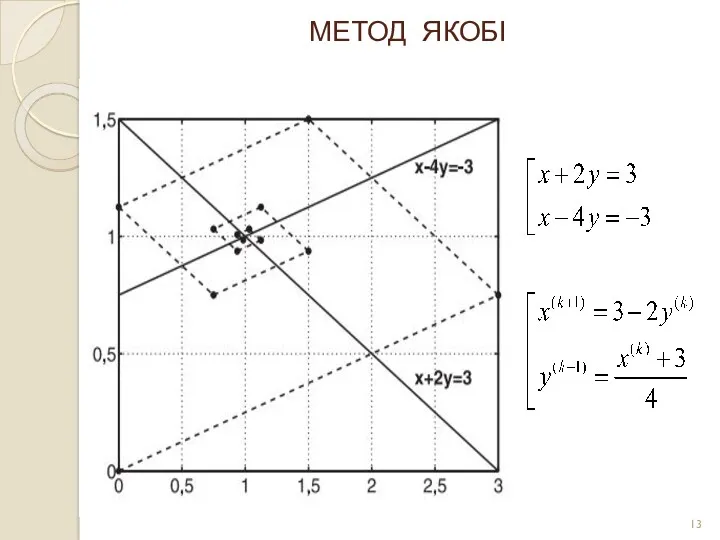
- 13. МЕТОД ЯКОБІ
- 14. МЕТОД ГАУССА-ЗЕЙДЕЛЯ Маємо (L + D)x = b - Ux У матричній формі метод Гаусса-Зейделя записується
- 17. ПОХИБКИ МЕТОДУ ГАУССА-ЗЕЙДЕЛЯ Локальна похибка за наближеннями, що отримані на двох сусідніх ітераціях Метод Гаусса-Зейделя слід
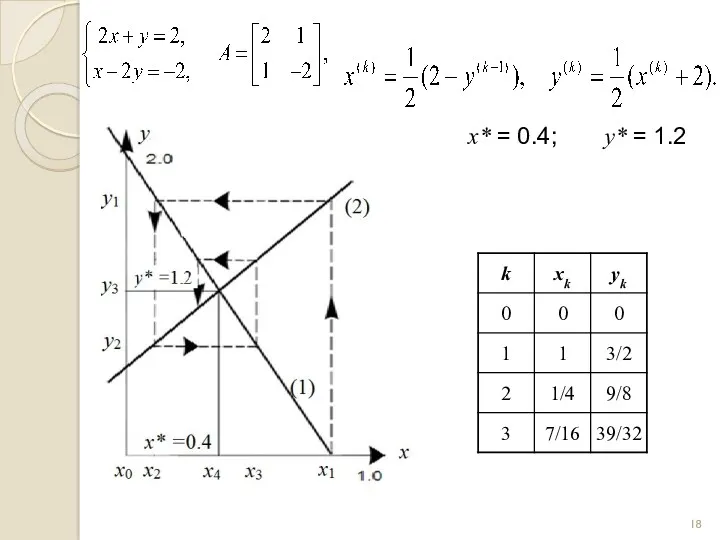
- 18. x* = 0.4; y* = 1.2
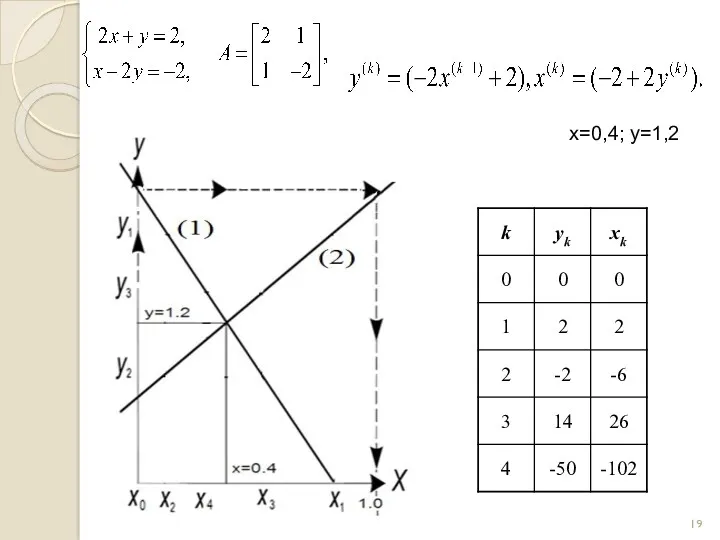
- 19. x=0,4; y=1,2
- 20. КАНОНІЧНА ФОРМА ІТЕРАЦІЙНИХ МЕТОДІВ Канонічною формою однокрокових ітераційних методів розв’язування СЛАР називається їх запис у вигляді:
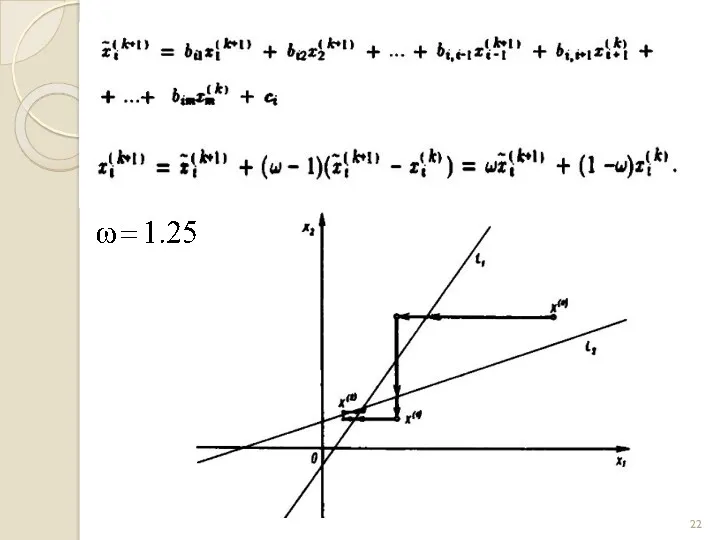
- 21. МЕТОД РЕЛАКСАЦІЇ Умови збіжності можна покращити, якщо ввести коефіцієнт демпфірування для врахування нев’язки Тоді метод простої
- 25. Метод релаксації
- 26. РОЗВ’ЯЗАННЯ СИСТЕМ НЕЛІНІЙНИХ РІВНЯНЬ У загальному випадку системa нелінійних рівнянь записується у вигляді де − функції
- 27. Для методу простої ітерації можна записати: де На першій ітерації на основі початкового наближення наступне знаходять
- 28. де – матриця Якобі, Одним із серйозних недоліків методу простих ітерацій є складність вибору функцій які
- 29. Узагальнений метод Ньютона:
- 34. Скачать презентацию























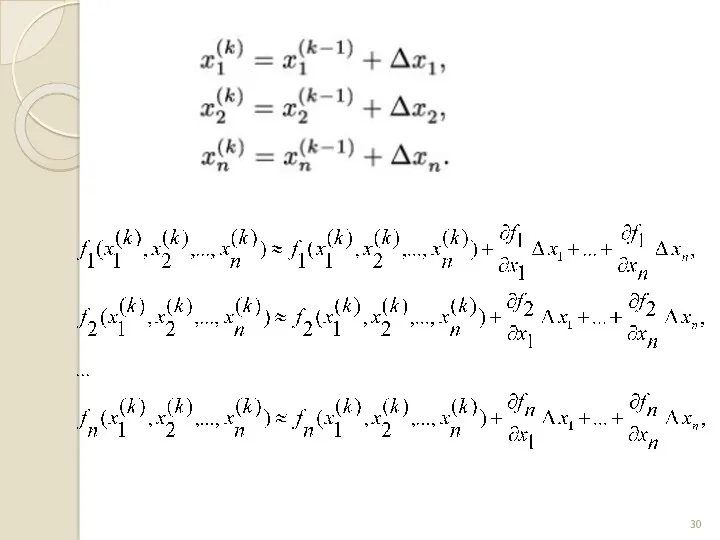

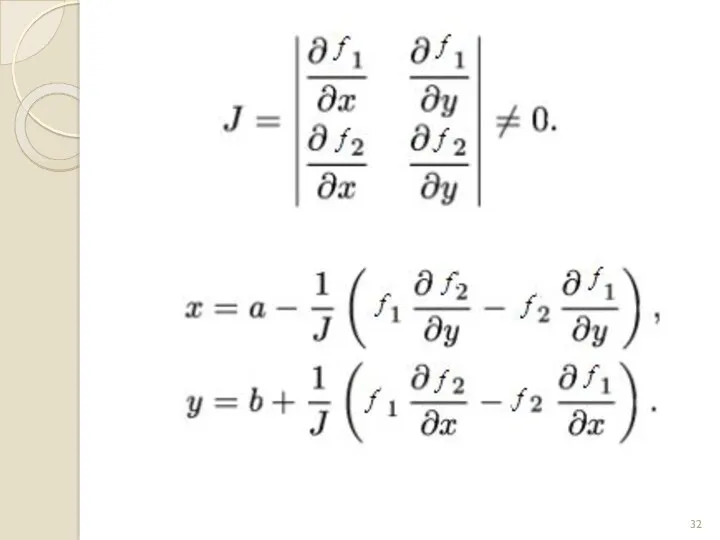
 Статистические ряды распределения и их виды
Статистические ряды распределения и их виды Вычисление первообразных функции
Вычисление первообразных функции Квадратные уравнения. Разработка раздела образовательной программы алгебры 8 класса
Квадратные уравнения. Разработка раздела образовательной программы алгебры 8 класса Разработка урока по математике.Письменное умножение двух чисел, оканчивающихся нулями
Разработка урока по математике.Письменное умножение двух чисел, оканчивающихся нулями Буквенное выражение
Буквенное выражение Умножение и деление смешанных чисел
Умножение и деление смешанных чисел Уравнение окружности
Уравнение окружности Открытый урок по математике Решение задач на увеличение числа в несколько единиц.
Открытый урок по математике Решение задач на увеличение числа в несколько единиц. Задачи городского тура олимпиады
Задачи городского тура олимпиады Изопериметрические задачи
Изопериметрические задачи Метрология, стандартизация и сертификация
Метрология, стандартизация и сертификация Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Сравнение чисел. 1 класс
Сравнение чисел. 1 класс Урок 11. Деление многозначного числа на многозначное с однозначным частным
Урок 11. Деление многозначного числа на многозначное с однозначным частным Практико–ориентированный подход в обучении математики
Практико–ориентированный подход в обучении математики Сложение чисел с помощью координатной прямой
Сложение чисел с помощью координатной прямой Тренажёр по математике (умножение на 6 и деление на 8)
Тренажёр по математике (умножение на 6 и деление на 8) Презентация Блоки Дьенеша
Презентация Блоки Дьенеша Четырехугольники. Подготовка к ОГЭ
Четырехугольники. Подготовка к ОГЭ Табличное умножение и деление, сложение и вычитание. Тренажёр
Табличное умножение и деление, сложение и вычитание. Тренажёр Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Презентация к конспекту занятия по формированию элементарных математических представлений на закрепление изученного материала для детей старшей группы
Презентация к конспекту занятия по формированию элементарных математических представлений на закрепление изученного материала для детей старшей группы Часть и целое
Часть и целое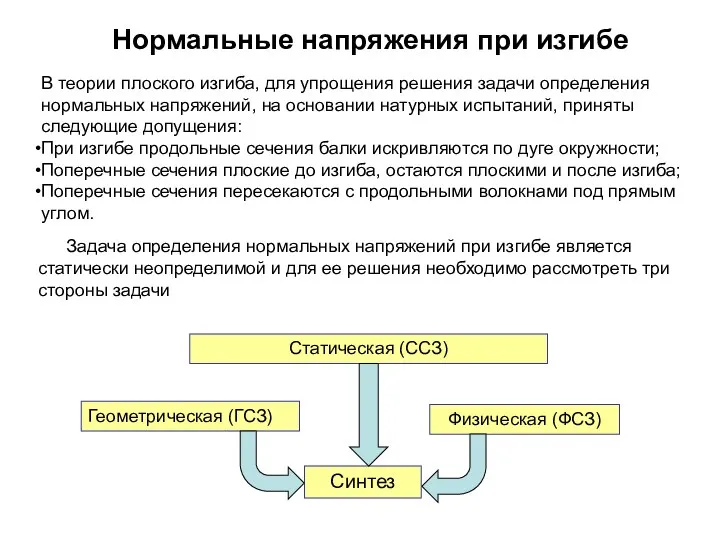 Нормальные напряжения при изгибе
Нормальные напряжения при изгибе Веселый счет
Веселый счет Математический диктант
Математический диктант История появления производной
История появления производной Счет в пределах 10, 1 класс Зимняя сказка
Счет в пределах 10, 1 класс Зимняя сказка