Содержание
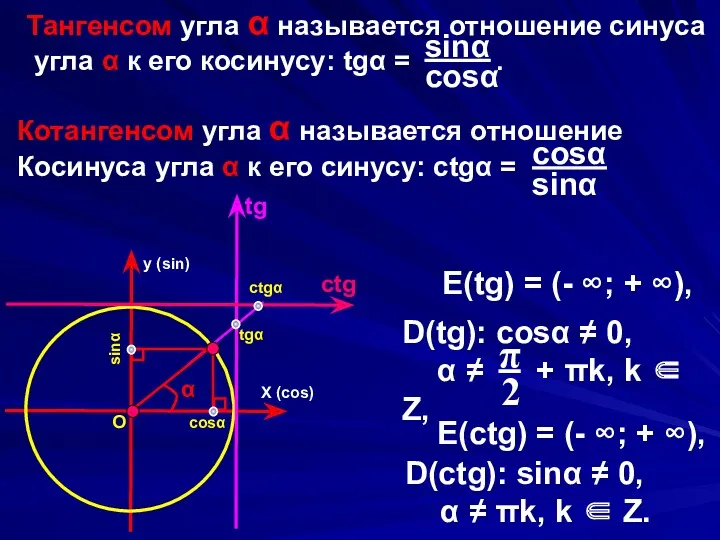
- 2. Синусом угла α называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол
- 3. X (cos) y (sin) α O cosα sinα E(tg) = (- ∞; + ∞), D(tg): cosα
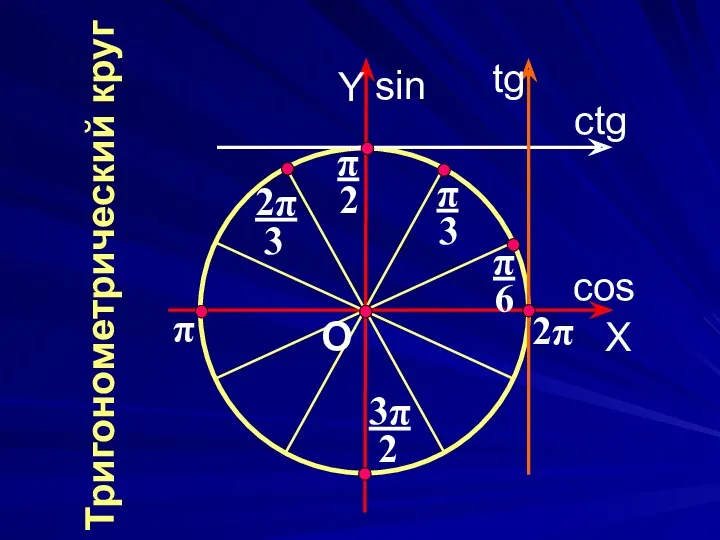
- 4. Y cos ctg tg sin X O π 2π Тригонометрический круг
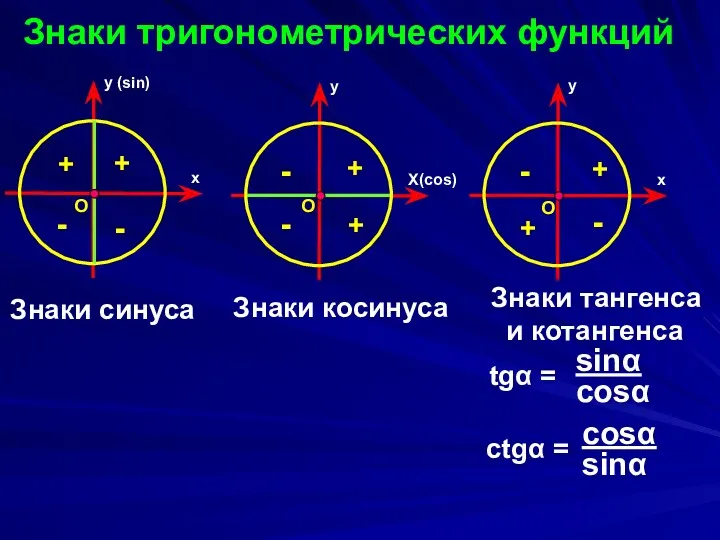
- 5. Знаки тригонометрических функций х y (sin) O Х(cos) y O х y O + + -
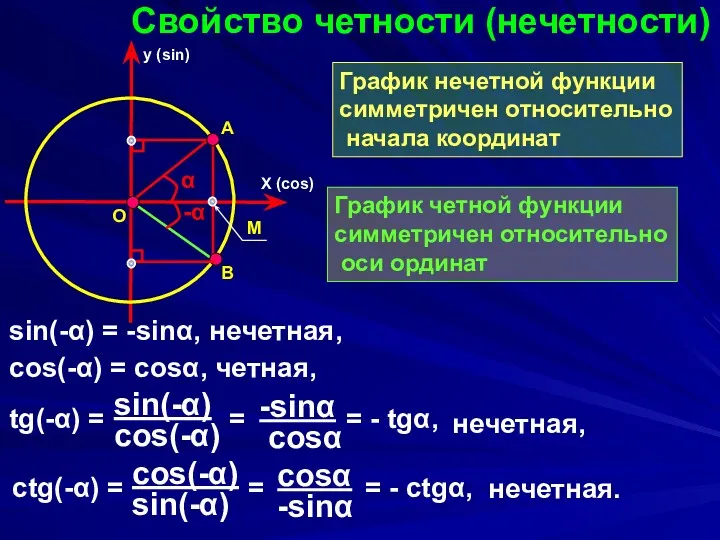
- 6. Свойство четности (нечетности) sin(-α) = -sinα, нечетная, X (cos) y (sin) α O -α А В
- 7. 1. Соотношения между тригонометрическими функциями одного и того же аргумента X (cos) sin2α + cos2α =
- 8. 1. Соотношения между тригонометрическими функциями одного и того же аргумента sin2α + cos2α = 1 ⎜
- 9. Формулы приведения Тригонометрические функции углов вида ± α, π ± α, ± α , 2π ±
- 10. Формулы приведения sin(π+α) = - sinα, X (cos) y (sin) α O А М π +
- 11. Формулы приведения sin(π - α) = sinα, X (cos) y (sin) α O А М π-α
- 12. Формулы приведения sin(2π+α) = sinα, X (cos) y (sin) α O А М 2π + α
- 13. Формулы приведения sin(2π - α) = - sinα, X (cos) y (sin) α O А М
- 14. Формулы приведения sin( + α) = cosα, X (cos) y (sin) α O А М В
- 15. Формулы приведения sin( - α) = cosα, X (cos) y (sin) α O А М В
- 16. Формулы приведения X (cos) y (sin) α O А М В N cos( + α) =
- 17. Формулы приведения X (cos) y (sin) α O А М В N cos( - α) =
- 18. 2. Формулы сложения и вычитания аргументов тригонометрических функций cos(α-β) = cosα • cosβ + sinα •
- 19. cos(α+β) = cosα • cosβ - sinα • sinβ sin(α+β) = sinα • cosβ + cosα
- 25. 3. Формулы двойных углов sin2α = 2sinα cosα sin2α = sin(α + α) = sinαcosα +
- 27. 4. Преобразование в произведение сумм sinα ± sinβ, cosα ± cosβ
- 28. 5. Формулы половинного аргумента
- 29. 6. Формулы универсальной подстановки
- 30. 7. Преобразование произведений в суммы или разности
- 31. 8. Преобразование выражений acosα + bsinα путем введения вспомогательного угла
- 32. Утверждение доказано
- 34. Скачать презентацию
















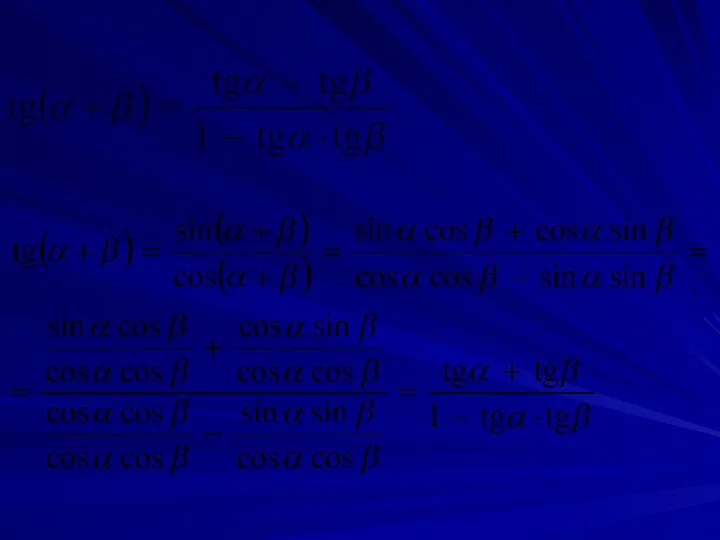
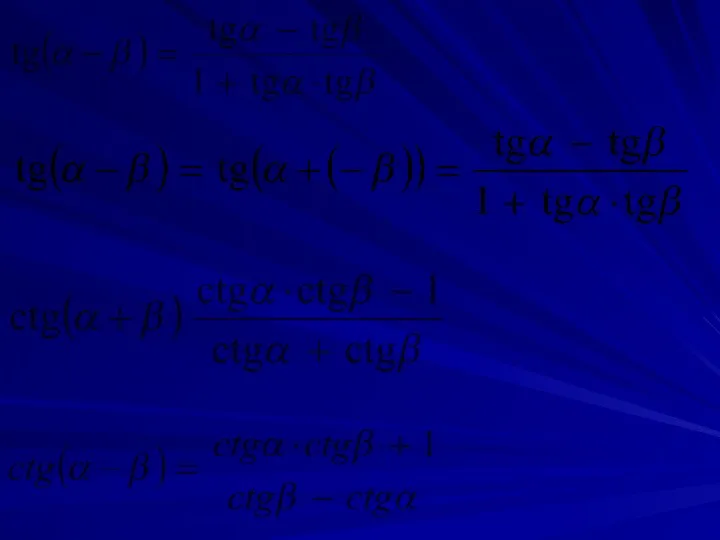









 Презентация к уроку- путешествию Вычитание трёхзначных чисел вида 804-467.
Презентация к уроку- путешествию Вычитание трёхзначных чисел вида 804-467. Равные треугольники. Высота, биссектриса, медиана
Равные треугольники. Высота, биссектриса, медиана Среднее арифметическое, размах и мода
Среднее арифметическое, размах и мода Презентация к внеклассному мероприятию: Математический КВН 3 класс
Презентация к внеклассному мероприятию: Математический КВН 3 класс Средняя линия треугольника
Средняя линия треугольника Абсолютті және қатысты шамалар
Абсолютті және қатысты шамалар Русские женщины-математики
Русские женщины-математики Презентация Длинный,короткий
Презентация Длинный,короткий Задачи на готовых чертежах
Задачи на готовых чертежах Урок математики в 4 классе. Школа России
Урок математики в 4 классе. Школа России Пифагор Самосский - великий древнегреческий математик
Пифагор Самосский - великий древнегреческий математик Плоские и пространственные кривые. Поверхности. (Лекция 8)
Плоские и пространственные кривые. Поверхности. (Лекция 8) число и цифра 7 УМК Л.В.Занков
число и цифра 7 УМК Л.В.Занков Радиус окружности, вписанной в равнобедренный прямоугольный
Радиус окружности, вписанной в равнобедренный прямоугольный Презентация к уроку математики 2 класс
Презентация к уроку математики 2 класс Плоскость, прямая, луч (5 класс)
Плоскость, прямая, луч (5 класс) Быстрый Поиск. Деревья поиска
Быстрый Поиск. Деревья поиска Площадь и периметр фигуры, составленной из двух-трёх прямоугольников (квадратов). Урок математики для учащихся 4 класса
Площадь и периметр фигуры, составленной из двух-трёх прямоугольников (квадратов). Урок математики для учащихся 4 класса Сборник логических заданий
Сборник логических заданий Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Математическое моделирование
Математическое моделирование Математика в задачах
Математика в задачах Великая Отечественная война. Исторические задачи
Великая Отечественная война. Исторические задачи Склад числа 9. Порівняння чисел у межах 9. Доповнення рівностей
Склад числа 9. Порівняння чисел у межах 9. Доповнення рівностей Счет десятками до 100 и обратно
Счет десятками до 100 и обратно Особенности работы со слабоуспевающими обучающимися на уроках математики
Особенности работы со слабоуспевающими обучающимися на уроках математики Математические ребусы
Математические ребусы Линейная функция и её график
Линейная функция и её график