Содержание
- 2. Возникновение понятия вектора. Векторный характер сил, скоростей, перемещений был знаком ещё в IV веке. Аристотель изображал
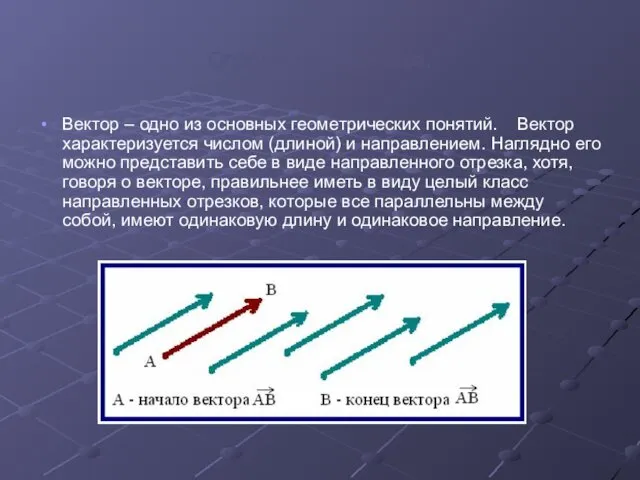
- 3. Определение вектора. Вектор – одно из основных геометрических понятий. Вектор характеризуется числом (длиной) и направлением. Наглядно
- 4. Равенство векторов. Любая точка является нулевым вектором. Длиной или модулем ненулевого вектора АВ называется длина АВ.
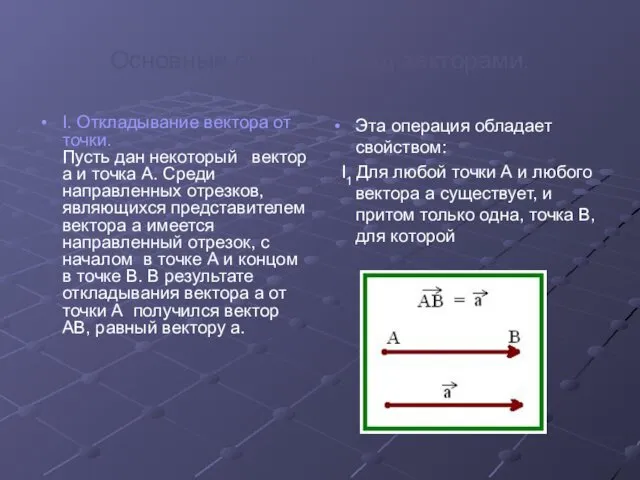
- 5. Основные операции над векторами. I. Откладывание вектора от точки. Пусть дан некоторый вектор а и точка
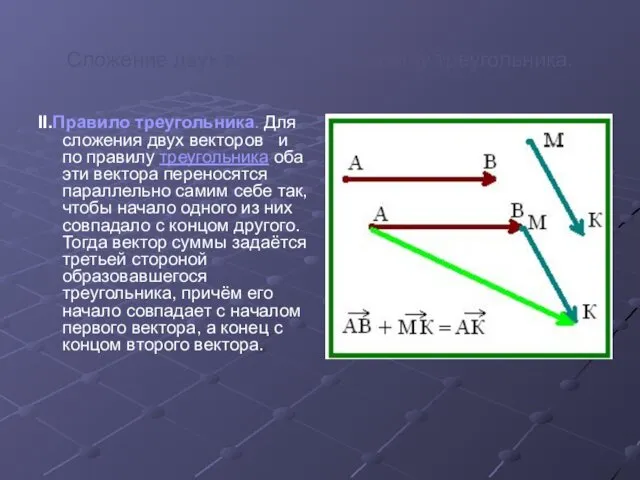
- 6. Сложение двух векторов по правилу треугольника. II.Правило треугольника. Для сложения двух векторов и по правилу треугольника
- 7. Сложение двух векторов по правилу параллелограмма. III.Если ненулевые векторы не параллельны, то их сумму удобно находить
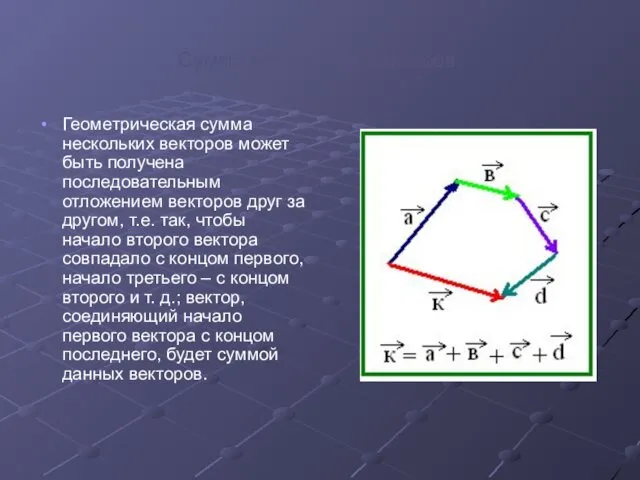
- 8. Сумма нескольких векторов. Геометрическая сумма нескольких векторов может быть получена последовательным отложением векторов друг за другом,
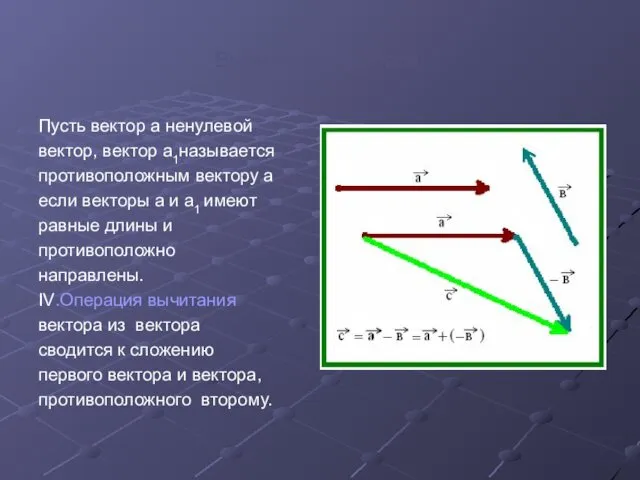
- 9. Вычитание векторов. Пусть вектор а ненулевой вектор, вектор а1называется противоположным вектору а если векторы а и
- 10. Умножение вектора на число. V. Произведением ненулевого вектора ā на число k называется такой вектор ū,
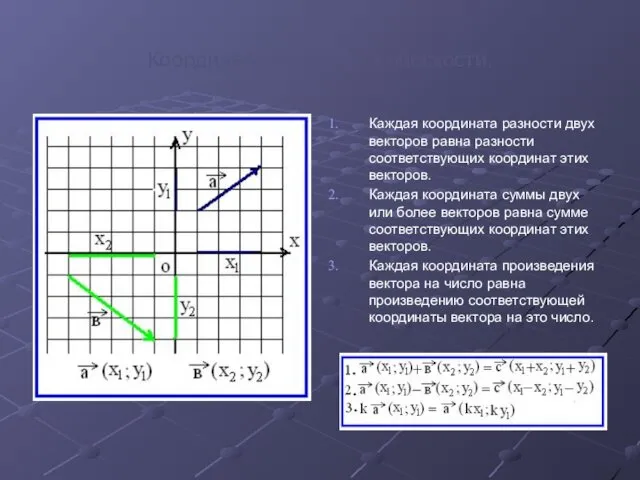
- 11. Координаты вектора на плоскости. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Каждая
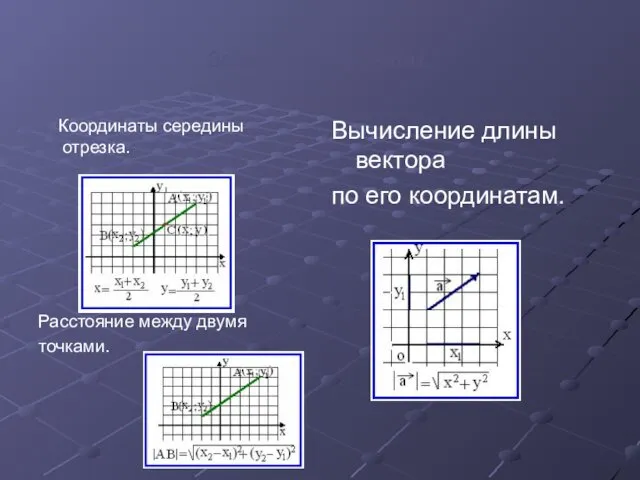
- 12. Задачи в координатах. Координаты середины отрезка. Расстояние между двумя точками. Вычисление длины вектора по его координатам.
- 13. Скалярное произведение векторов. Определение. Скалярным произведением двух векторов называется произведение их длин на косинус угла между
- 14. Векторы в физике. В физике практически всегда речь идёт не о математических объектах (обладающих теми или
- 15. Перемещение. Для решения различных практических задач в разных сферах деятельности ( например, в диспетчерской службе наземного
- 16. Ускорение. Ускорением тела при его равноускоренном движении называется величина, равная отношению измерения скорости к промежутку времени,
- 17. Магнитная индукция. Многие замечали, что одни магниты создают в пространстве более сильные поля, чем другие. Магнитное
- 19. Скачать презентацию









 Arvutusülesanded ühe osaleva aine järgi
Arvutusülesanded ühe osaleva aine järgi Среднее арифметическое
Среднее арифметическое Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Остров “Решайка”. Остров “Мыслите
Остров “Решайка”. Остров “Мыслите Производная. Понятие производной. Производная частных функций
Производная. Понятие производной. Производная частных функций Многоугольники, вписанные в окружность. Геометрия, 8 класс
Многоугольники, вписанные в окружность. Геометрия, 8 класс Дисперсионный анализ
Дисперсионный анализ Делимость суммы и разности чисел. Урок 102
Делимость суммы и разности чисел. Урок 102 Свойство биссектрисы угла
Свойство биссектрисы угла ОГЭ по математике. Задание 1-5
ОГЭ по математике. Задание 1-5 Пропорциональность
Пропорциональность Множество действительных чисел
Множество действительных чисел Основы метрологии, стандартизации, сертификации и контроля качества
Основы метрологии, стандартизации, сертификации и контроля качества Графы. Вершина. Ребро. Представление задачи с помощью графов
Графы. Вершина. Ребро. Представление задачи с помощью графов Математический бой. 6 класс
Математический бой. 6 класс Розв’язання вправ. Квадратне рівняння
Розв’язання вправ. Квадратне рівняння Многоугольники
Многоугольники Исторические комбинаторные задачи. Различные комбинации трех элементов
Исторические комбинаторные задачи. Различные комбинации трех элементов Единицы длины. 5 класс
Единицы длины. 5 класс Что такое дробь?
Что такое дробь? Сравнение натуральных чисел. Математика 5 класс
Сравнение натуральных чисел. Математика 5 класс Математика на повторення (зимові канікули).
Математика на повторення (зимові канікули). Прямая пропорциональность. Актуализация опорных знаний
Прямая пропорциональность. Актуализация опорных знаний Решение задач и выражений
Решение задач и выражений Специфика возникновения нормального распределения применительно к объектам биологии и медицины
Специфика возникновения нормального распределения применительно к объектам биологии и медицины Диагностическая работа. Готовимся к ГИА. 9 класс
Диагностическая работа. Готовимся к ГИА. 9 класс Адаптивные фильтры. Практическое применение (2)
Адаптивные фильтры. Практическое применение (2) Числовые последовательности
Числовые последовательности