Содержание
- 2. Section 1.3 p 1.3 Separable ODEs. Modeling
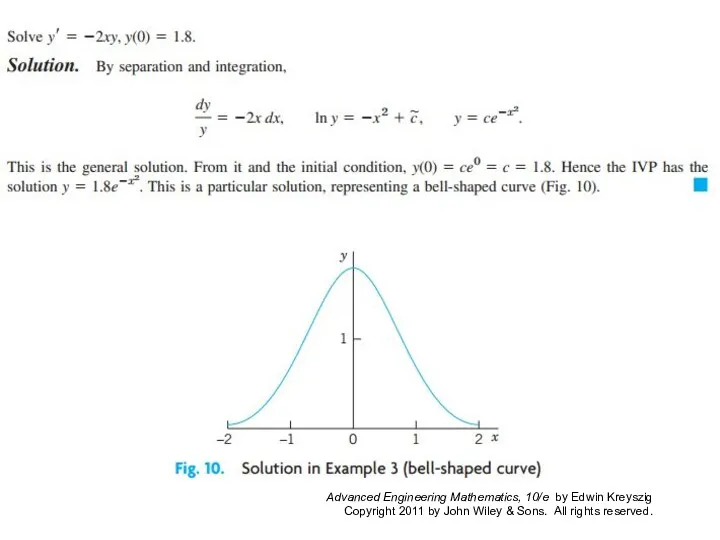
- 3. Section 1.3 p Many practically useful ODEs can be reduced to the form (1) g(y) y’
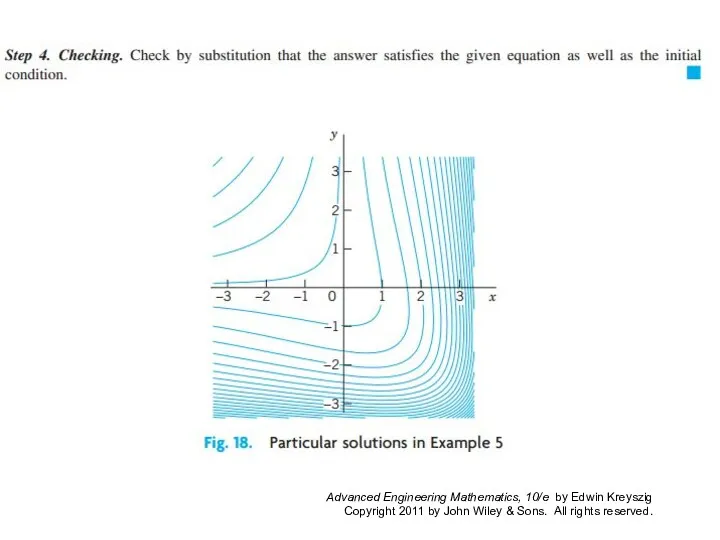
- 14. EXAMPLE 5 Mixing Problem Mixing problems occur quite frequently in chemical industry. We explain here how
- 15. EXAMPLE 5 (continued) Solution. Step 1. Setting up a model. Let y(t) denote the amount of
- 16. EXAMPLE 5 (continued) Step 2. Solution of the model. The ODE (4) is separable. Separation, integration,
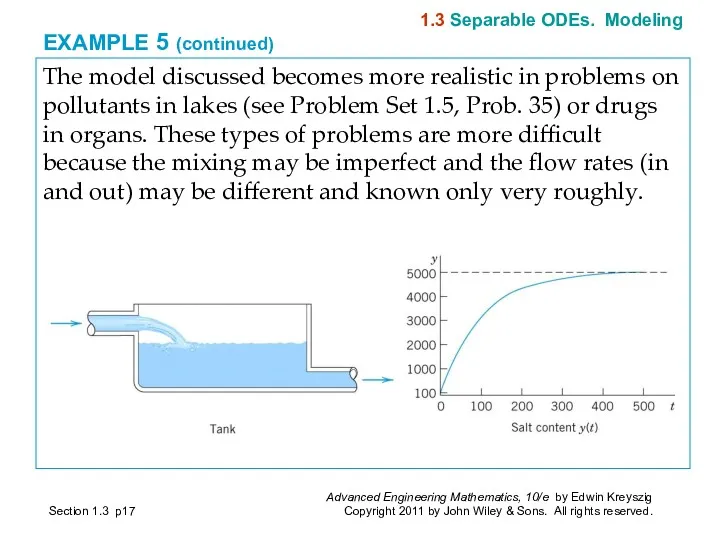
- 17. EXAMPLE 5 (continued) The model discussed becomes more realistic in problems on pollutants in lakes (see
- 18. Certain non separable ODEs can be made separable by transformations that introduce for y a new
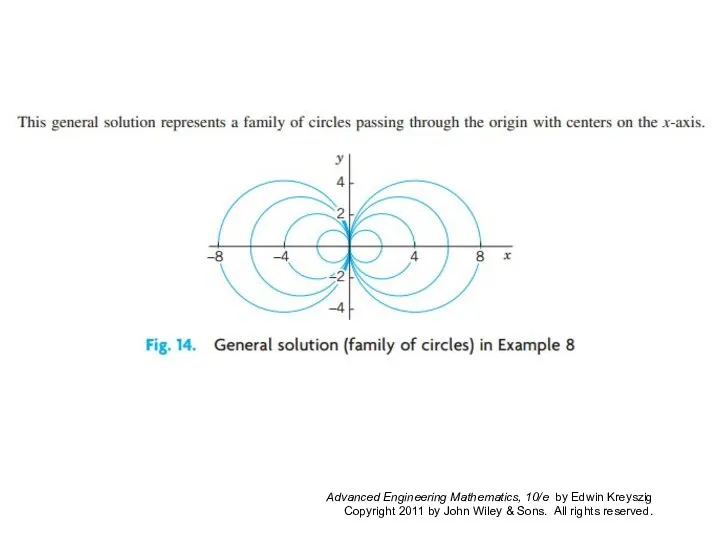
- 19. The form of such an ODE suggests that we set y/x = u; thus, (9) y
- 24. Section 1.4 p 1.4 Exact ODEs. Integrating Factors
- 25. We recall from calculus that if a function u(x, y) has continuous partial derivatives, its differential
- 26. A first-order ODE M(x, y) + N(x, y)y’ = 0, written as (use dy = y’dx
- 27. This is called an implicit solution, in contrast to a solution y = h(x) as defined
- 28. Let M and N be continuous and have continuous first partial derivatives in a region in
- 29. This condition is not only necessary but also sufficient for (1) to be an exact differential
- 31. Example
- 36. We multiply a given nonexact equation, (12) P(x, y) dx + Q(x, y) dy = 0,
- 37. For M dx + N dy = 0 the exactness condition (5) is ∂M/∂y = ∂N/∂x.
- 38. Let F = F(x). Then Fy = 0, and Fx = F’ = dF/dx, so that
- 39. Section 1.4 p Theorem 1 Integrating Factor F(x) If (12) is such that the right side
- 40. Similarly, if F* = F*(y), then instead of (16) we get (18) Section 1.4 p 1.4
- 41. Section 1.4 p Theorem 2 Integrating Factor F*(y) If (12) is such that the right side
- 50. Section 1.5 p 1.5 Linear ODEs. Bernoulli Equation. Population Dynamics
- 51. A first-order ODE is said to be linear if it can be brought into the form
- 52. Homogeneous Linear ODE. We want to solve (1) on some interval a (2) y’ + p(x)y
- 53. Nonhomogeneous Linear ODE We now solve (1) in the case that r(x) in (1) is not
- 55. EXAMPLE 1 First-Order ODE, General Solution, Initial Value Problem Solve the initial value problem y’ +
- 56. Numerous applications can be modeled by ODEs that are nonlinear but can be transformed to linear
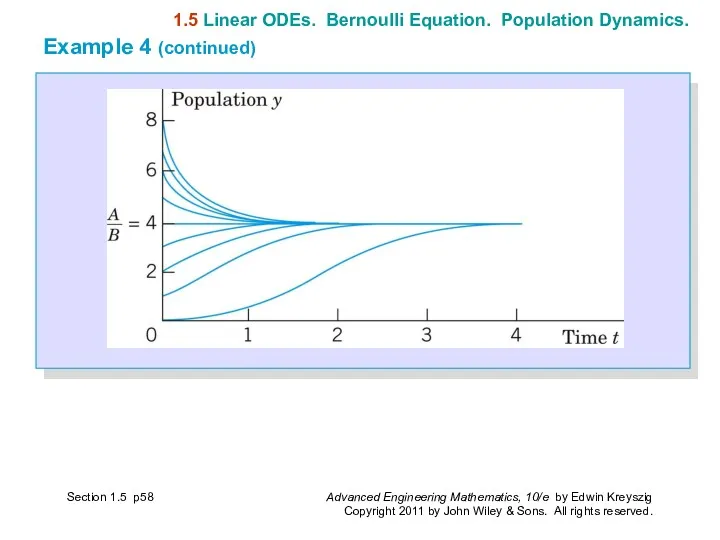
- 57. Logistic Equation Solve the following Bernoulli equation, known as the logistic equation (or Verhulst equation) (11)
- 58. 1.5 Linear ODEs. Bernoulli Equation. Population Dynamics. Section 1.5 p Example 4 (continued)
- 59. SUMMARY OF CHAPTER 1 First-Order ODEs Section 1.Summary p
- 60. Section 1.Summary p SUMMARY OF CHAPTER 1 First-Order ODEs This chapter concerns ordinary differential equations (ODEs)
- 61. Section 1.Summary p SUMMARY OF CHAPTER 1 First-Order ODEs (continued 1) A first-order ODE usually has
- 62. Section 1.Summary p SUMMARY OF CHAPTER 1 First-Order ODEs (continued 2) A separable ODE is one
- 64. Скачать презентацию






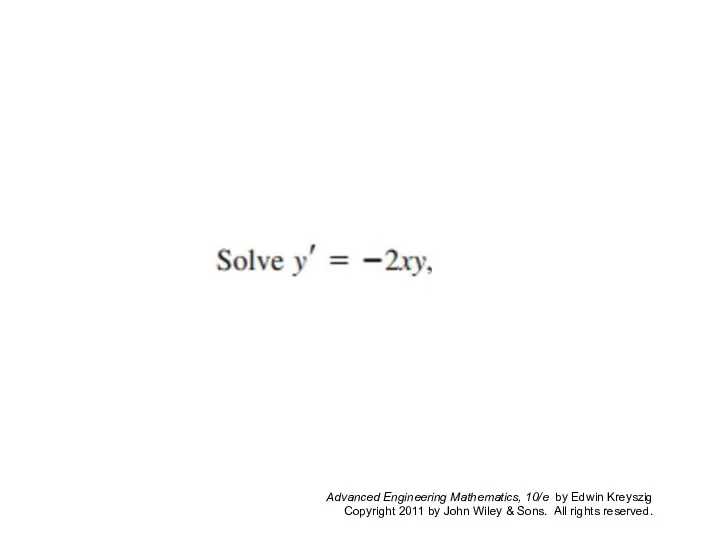









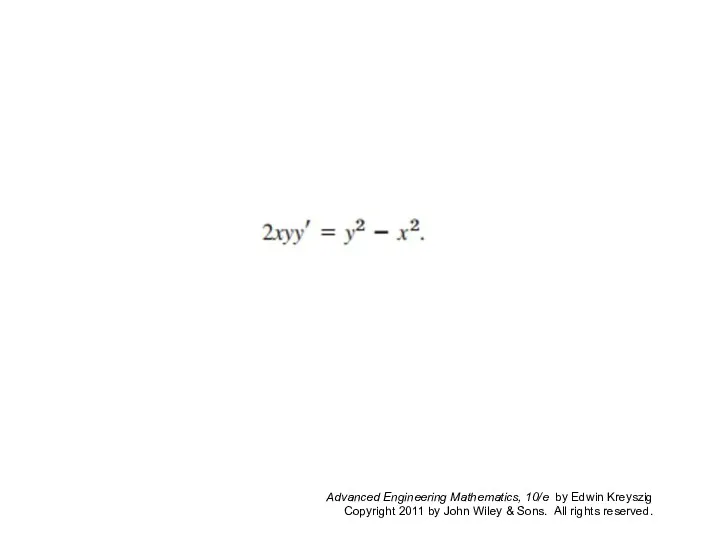































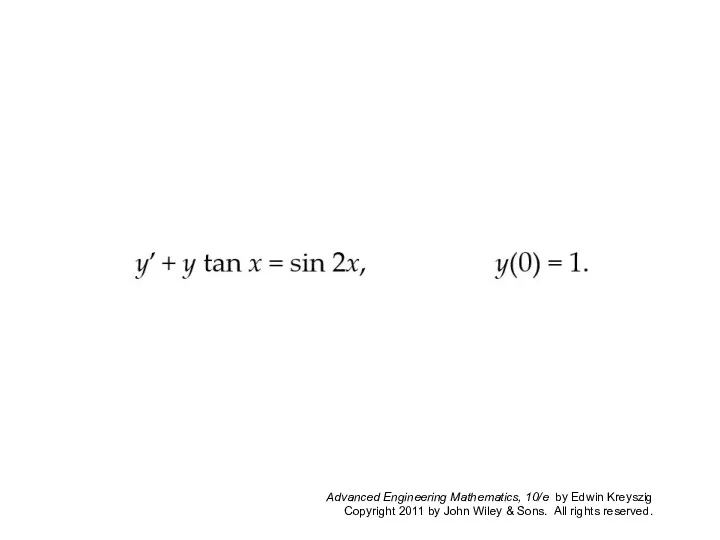







 Виртуальная экскурсия на мемориал Защитникам Ленинграда
Виртуальная экскурсия на мемориал Защитникам Ленинграда Московский городской конкурс исследовательских и проектных работ обучающихся
Московский городской конкурс исследовательских и проектных работ обучающихся Типы проектов. Структура индивидуального проекта
Типы проектов. Структура индивидуального проекта Порядок проведения итогового сочинения (изложения) в 2019-2020 учебном году
Порядок проведения итогового сочинения (изложения) в 2019-2020 учебном году Итоги проведения ГИА-2016. Подготовка к государственной итоговой аттестации в 2017 году
Итоги проведения ГИА-2016. Подготовка к государственной итоговой аттестации в 2017 году Презентация Самостоятельная работа на уроках русского языка
Презентация Самостоятельная работа на уроках русского языка Технология проектной деятельности: структура и содержание проекта
Технология проектной деятельности: структура и содержание проекта Одеська Національна Академія Харчових Технологій
Одеська Національна Академія Харчових Технологій Рефлексия как этап современного урока в условиях ФГОС
Рефлексия как этап современного урока в условиях ФГОС Программа развития учителей будущего Next–Педагог
Программа развития учителей будущего Next–Педагог Подготовка, выполнение и защита выпускной квалификационной работы
Подготовка, выполнение и защита выпускной квалификационной работы Развитие поликультурного образования в России
Развитие поликультурного образования в России Лекция как форма обучения
Лекция как форма обучения Квиз. Своя игра
Квиз. Своя игра Вчимося читати
Вчимося читати Требования к современному уроку в рамках ФГОС
Требования к современному уроку в рамках ФГОС Внедрение дополнительных общеобразовательных программ для подростков с ограниченными возможностями здоровья
Внедрение дополнительных общеобразовательных программ для подростков с ограниченными возможностями здоровья Профессиональный стандарт педагога в начальной школе
Профессиональный стандарт педагога в начальной школе Системно-деятельностный подход в обучении младшего школьника
Системно-деятельностный подход в обучении младшего школьника Правила оформления курсовой работы. Программирование на языке высокого уровня
Правила оформления курсовой работы. Программирование на языке высокого уровня Отчет о прохождении летней практики
Отчет о прохождении летней практики Федеральные основные образовательные программы
Федеральные основные образовательные программы Английский язык для будущих военных
Английский язык для будущих военных Презентация к теме самообразования Тестирование в начальных классах как способ повышения качества обучения
Презентация к теме самообразования Тестирование в начальных классах как способ повышения качества обучения CV Writing
CV Writing О региональных проектах национального проектаОбразование
О региональных проектах национального проектаОбразование Концепция духовно-нравственного развития и воспитания личности гражданина России (образовательная система Школа 2100)
Концепция духовно-нравственного развития и воспитания личности гражданина России (образовательная система Школа 2100) Президиум №16 от 29.11.2019 года Азовской организации профсоюза работников народного образования и науки РФ
Президиум №16 от 29.11.2019 года Азовской организации профсоюза работников народного образования и науки РФ