Содержание
- 2. Why a separator? Open circuit grinding is not very efficient: Overgrinding of fines Useless for quality
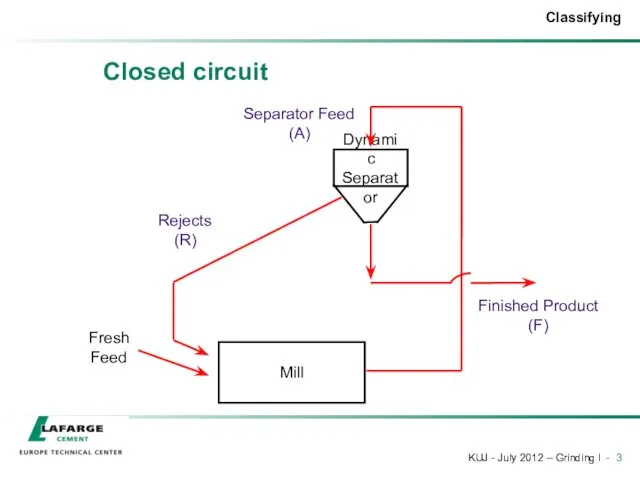
- 3. Closed circuit
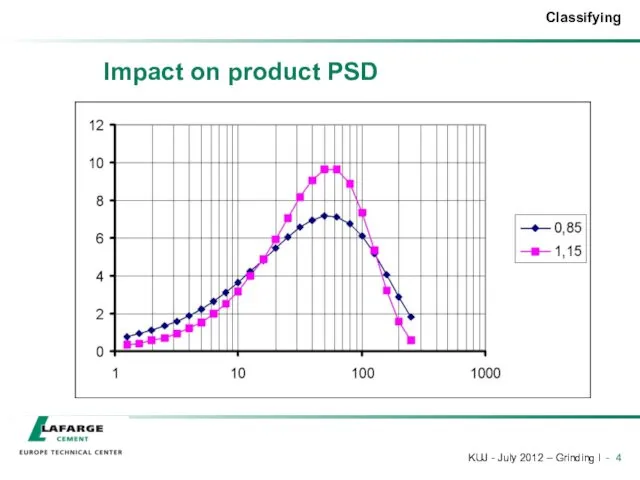
- 4. Impact on product PSD
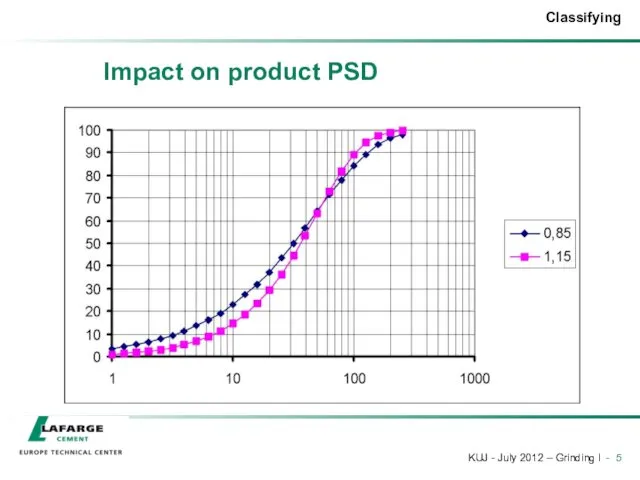
- 5. Impact on product PSD
- 6. Separation in general A SEPARATOR DOES NOT GRIND !!! … but it helps optimize the efficiency
- 7. Circulating Load (CL) How can we determine it? C.L. = R/F (used by Lafarge) Others define
- 8. Separation efficiency How do we assess the efficiency of separation? The tool is the separation curve,
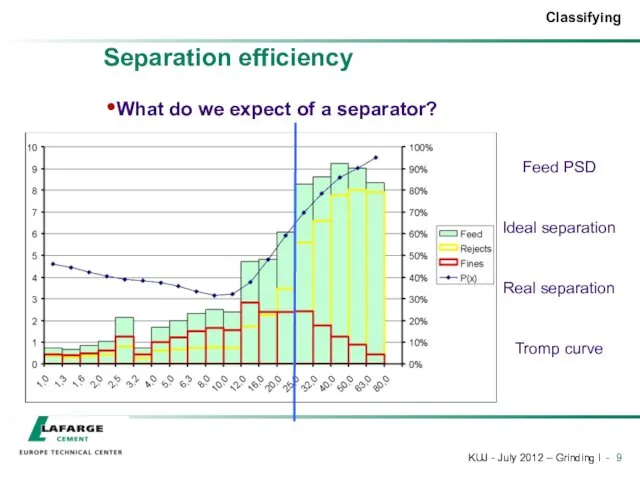
- 9. Separation efficiency What do we expect of a separator? Feed PSD Ideal separation Real separation Tromp
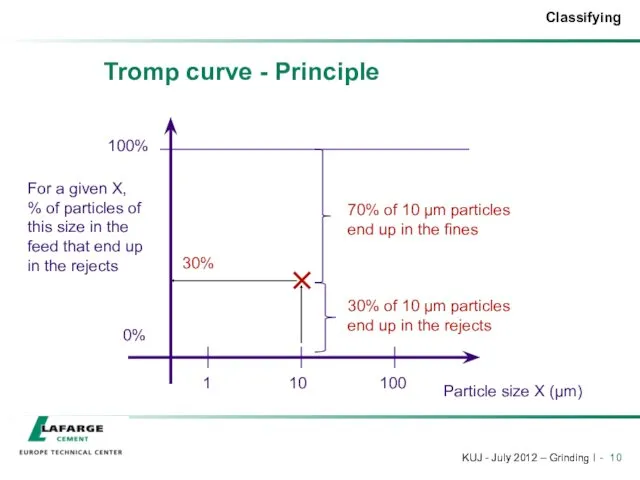
- 10. Tromp curve - Principle Particle size X (µm) For a given X, % of particles of
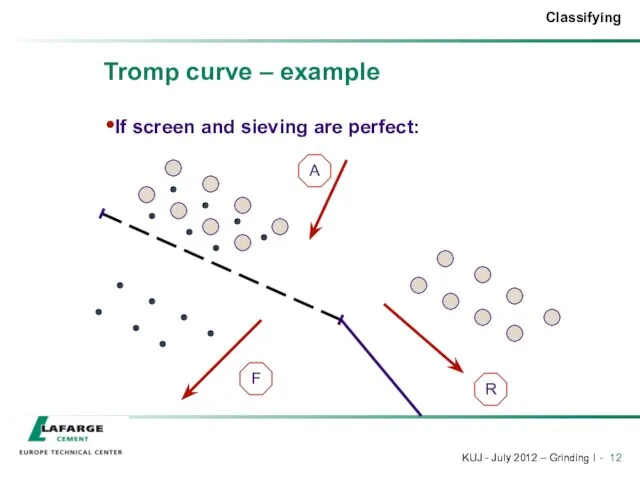
- 11. Tromp curve – example Let’s take the example of a sieve:
- 12. Tromp curve – example If screen and sieving are perfect: A F R
- 13. Tromp curve – Perfect screen 50µm Above 50 µm, all particles end up in the rejects
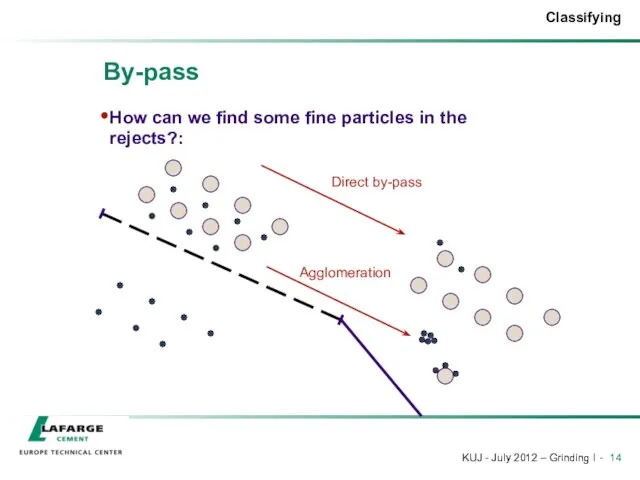
- 14. By-pass How can we find some fine particles in the rejects?:
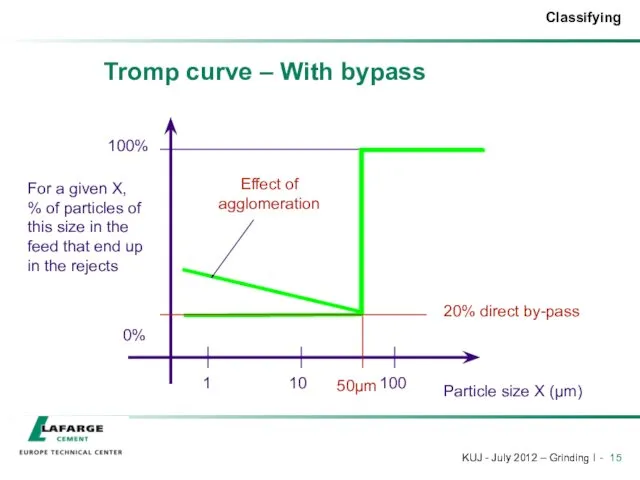
- 15. Tromp curve – With bypass 50µm 20% direct by-pass
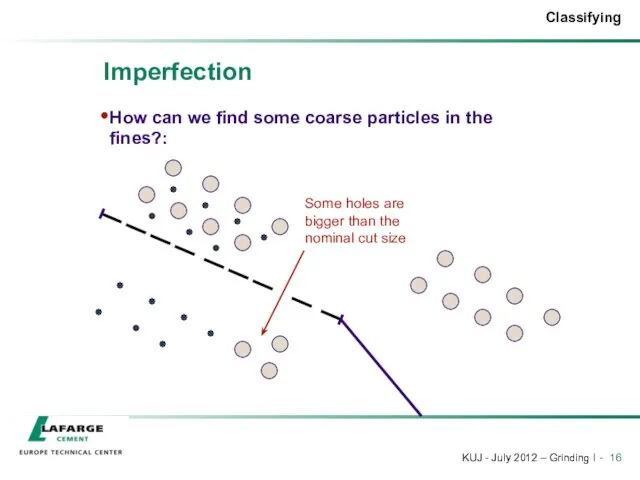
- 16. Imperfection How can we find some coarse particles in the fines?:
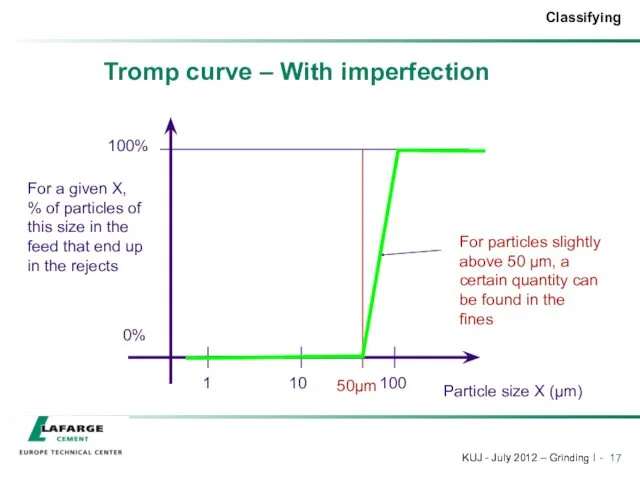
- 17. Tromp curve – With imperfection 50µm For particles slightly above 50 µm, a certain quantity can
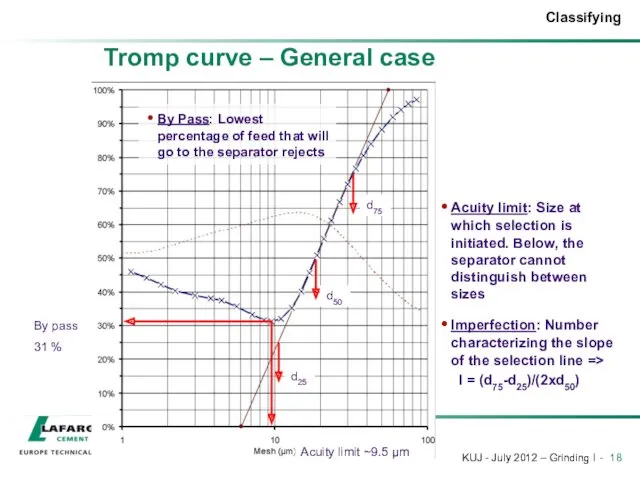
- 18. Tromp curve – General case By Pass: Lowest percentage of feed that will go to the
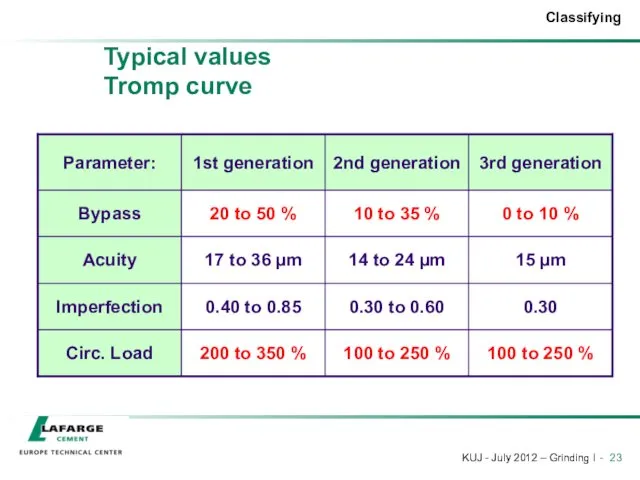
- 19. Tromp curve - Interpretation By-pass Should be as low as possible Directly linked to separator efficiency:
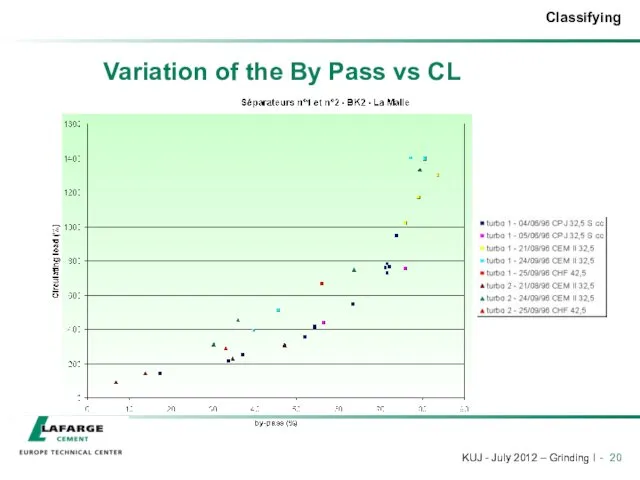
- 20. Variation of the By Pass vs CL
- 21. Tromp curve - Interpretation Acuity limit Mainly depends on the fineness of final product Imperfection Should
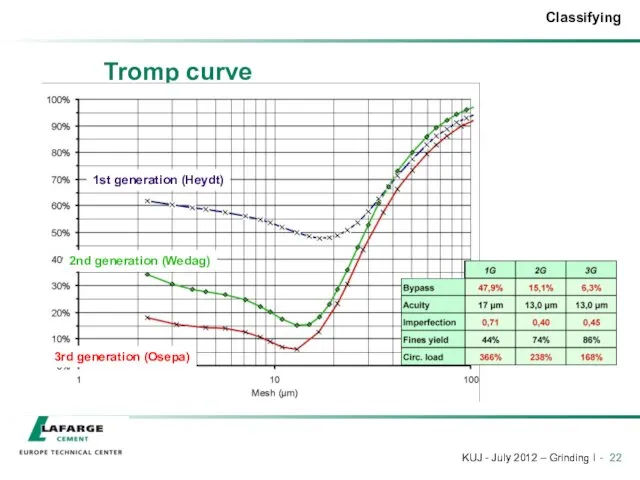
- 22. Tromp curve 1st generation (Heydt) 2nd generation (Wedag) 3rd generation (Osepa)
- 23. Typical values Tromp curve
- 24. Building a Tromp curve Mass balance Knowledge of a physical property of 3 flows gives access
- 25. Tromp curve: notations Separator Feed Fines Rejects A = feed flow (t/h) ax = % of
- 26. Tromp curves – R/A calculation Global mass balance: A = R + F (1) inlet flow
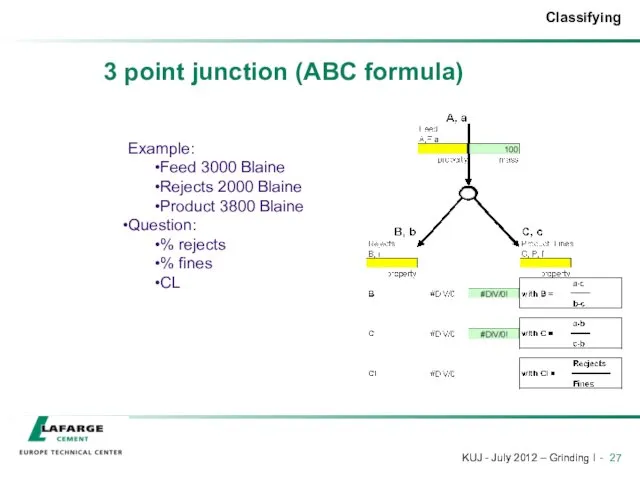
- 27. 3 point junction (ABC formula) Example: Feed 3000 Blaine Rejects 2000 Blaine Product 3800 Blaine Question:
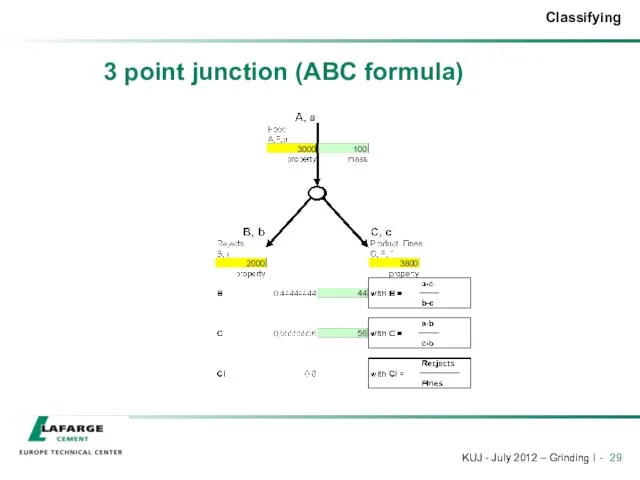
- 28. 3 point junction (ABC formula) Example: Feed 3000 Blaine Rejects 2000 Blaine Product 3800 Blaine Question:
- 29. 3 point junction (ABC formula)
- 30. Tromp curves – R/A calculation Interpretation: Using the laser PSD for separator feed, rejects and fines,
- 31. Tromp curves – average R/A From all the values of R/A calculated before (one for each
- 32. Tromp curves – final calculation From equations (1) and (2): A = R + F and
- 34. Скачать презентацию















 Викторина Жизнь и творчество С.А. Есенина
Викторина Жизнь и творчество С.А. Есенина Характеристика методов диагностики заболевания и контроля за эффективностью и безопасностью применения лекарственных средств
Характеристика методов диагностики заболевания и контроля за эффективностью и безопасностью применения лекарственных средств Модульная технология обучения на уроках биологии
Модульная технология обучения на уроках биологии ФГОС - презентация
ФГОС - презентация Brawlhalla и её движок
Brawlhalla и её движок Плата сбора данных ЛА 2М3
Плата сбора данных ЛА 2М3 Анализаторы, их строение и функции
Анализаторы, их строение и функции Оформление сертификатов
Оформление сертификатов Психологические механизмы волевой регуляции. В. А. Иванников
Психологические механизмы волевой регуляции. В. А. Иванников Инструкция по выгодной продаже недвижимости от АН Держава
Инструкция по выгодной продаже недвижимости от АН Держава Будущее робототехники. История появления и развития, предназначение и перспективы робототехники
Будущее робототехники. История появления и развития, предназначение и перспективы робототехники кл Безопасность в социальных сетях
кл Безопасность в социальных сетях формирование ключевых компетенций учащихся на уроках химии как средство реализации личностно-ориентированного подхода в образовании.
формирование ключевых компетенций учащихся на уроках химии как средство реализации личностно-ориентированного подхода в образовании. Аудит кредитных операций
Аудит кредитных операций Образцовый Театр Моды Стиль, коллекция Овощной микс
Образцовый Театр Моды Стиль, коллекция Овощной микс Презентация. МАСТЕР- КЛАСС.Чудеса солёного теста.
Презентация. МАСТЕР- КЛАСС.Чудеса солёного теста. Возрастные особенности шестиклассников
Возрастные особенности шестиклассников презентация на тему: Совершенствование системы физкультурно-оздоровительной работы...
презентация на тему: Совершенствование системы физкультурно-оздоровительной работы... Прием в 1 класс
Прием в 1 класс Презентация по ПДД
Презентация по ПДД Флуктуации амплитуды и частоты в автогенераторах СВЧ
Флуктуации амплитуды и частоты в автогенераторах СВЧ Великобритания
Великобритания Искусство Японии
Искусство Японии Электрические нагрузки промышленных предприятий. Номинальные режимы работы ЭП
Электрические нагрузки промышленных предприятий. Номинальные режимы работы ЭП Жизнь птиц и зверей
Жизнь птиц и зверей Эвенки – народы Байкала
Эвенки – народы Байкала Презентация Окислительные свойства азотной кислоты
Презентация Окислительные свойства азотной кислоты Игра в черное и белое
Игра в черное и белое