Содержание
- 2. Тема урока: Формулы корней квадратных уравнений. Цель урока: обобщить и систематизировать основные знания и умения по
- 3. Рене Декарт (французский математик) «Для разыскания истины вещей необходим метод»
- 4. Полезно знать: Исторические сведения: Квадратные уравнения впервые встречаются в работе индийского математика и астронома Ариабхатты. Другой
- 5. Устная работа Для того чтобы включиться в работу и сконцентрироваться предлагаю вам небольшую устную разминку. Для
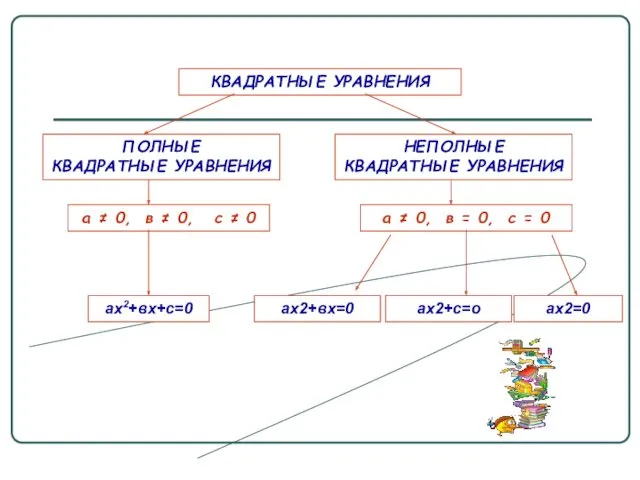
- 6. ПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ КВАДРАТНЫЕ УРАВНЕНИЯ а ≠ 0, в ≠ 0, с ≠
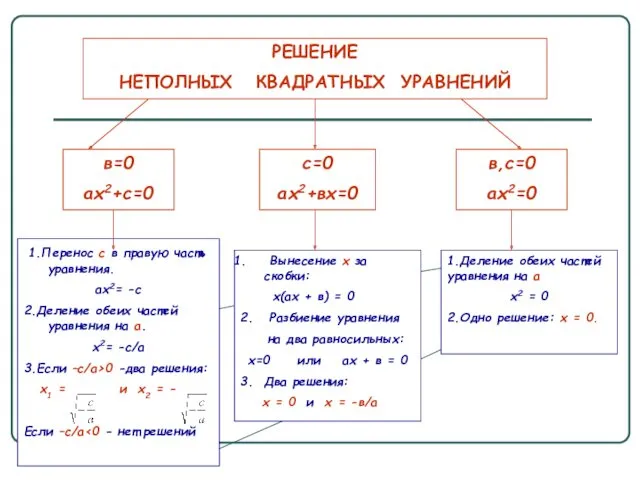
- 7. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ в=0 ах2+с=0 с=0 ах2+вх=0 в,с=0 ах2=0 1.Перенос с в правую часть уравнения.
- 8. Тест ( 2мин) взаимопроверка а) х2 +6 х + 3 = 0 б) 2 х2 +
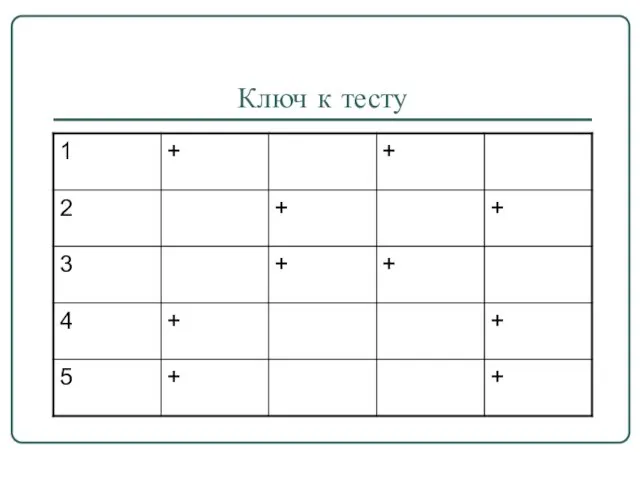
- 9. Ключ к тесту
- 10. А теперь, ребята , расскажите алгоритм решения полного квадратного уравнения.
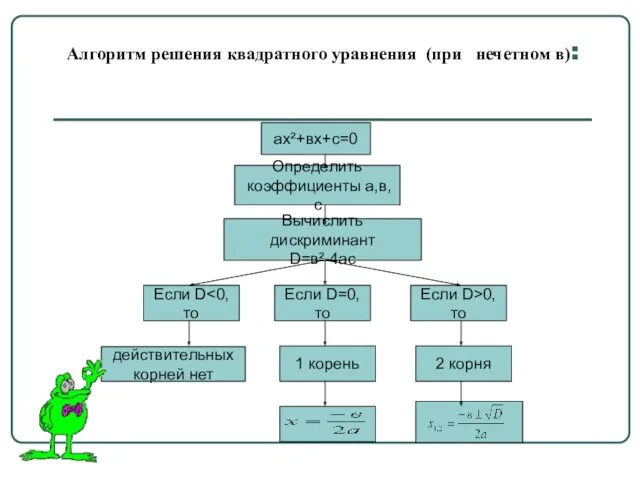
- 11. Алгоритм решения квадратного уравнения (при нечетном в): ах²+вх+с=0 Определить коэффициенты а,в,с Если D Вычислить дискриминант D=в²-4ас
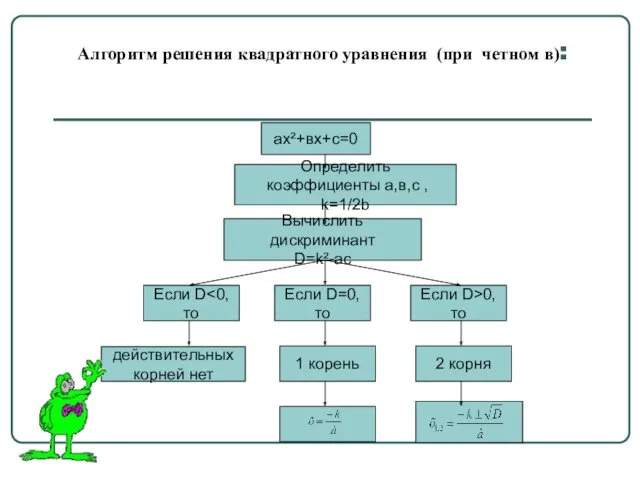
- 12. Алгоритм решения квадратного уравнения (при четном в): ах²+вх+с=0 Определить коэффициенты а,в,с , k=1/2b Если D Вычислить
- 13. Ф И З К У Л Ь Т - М И Н У Т К А
- 14. Актуализация знаний 1. x2 – 7х +6 = 0 1. 8х2 -6 х +1=0 1. 2.
- 15. Повторение. Соотнесите функцию с графиком
- 16. Рефлексия Могу решать уравнения самостоятельно Нужна помощь при решении уравнений Совсем не могу решать уравнения
- 17. Домашнее задание П. 25 №25.4 (ОРО) № 25.37(а,б), № 25.43 Итог урока обобщили и систематизировали основные
- 19. Скачать презентацию











 Классный часСвятая мать добром спасет
Классный часСвятая мать добром спасет Презентация Развитие способностей и творческого потенциала всех детей в условиях реализации ФГОС ДО
Презентация Развитие способностей и творческого потенциала всех детей в условиях реализации ФГОС ДО Клещевой энцифалит
Клещевой энцифалит Этимология химических элементов
Этимология химических элементов 20240130_17._delenie
20240130_17._delenie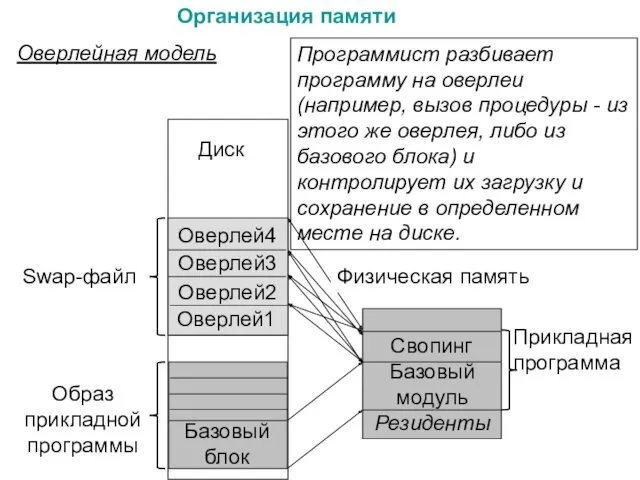 Организация памяти. (Лекция 5, 6)
Организация памяти. (Лекция 5, 6) Особенности обучения взрослых и рекомендации по проведению тренинга
Особенности обучения взрослых и рекомендации по проведению тренинга Европейский иррационализм
Европейский иррационализм Роль религии в жизни общества
Роль религии в жизни общества Пространственная жесткость одноэтажных промышленных зданий
Пространственная жесткость одноэтажных промышленных зданий Бази даних. Поняття звіту. Автоматичне створення звіту
Бази даних. Поняття звіту. Автоматичне створення звіту презентация Автоматизация звука С
презентация Автоматизация звука С 20231008_maslenitsa1
20231008_maslenitsa1 Детские праздники и дни рождения Лазертаг
Детские праздники и дни рождения Лазертаг ВКР: Реконструкции системы электроснабжения ОАО Балашихинский литейно-механический завод
ВКР: Реконструкции системы электроснабжения ОАО Балашихинский литейно-механический завод Урок по природе и экологии Красноярского края – 5 класс: Природные системы Красноярского края.
Урок по природе и экологии Красноярского края – 5 класс: Природные системы Красноярского края. Проект Безопасность детей через ознакомление с правилами дорожного движения
Проект Безопасность детей через ознакомление с правилами дорожного движения Рельеф Земли. Равнины суши. Горы суши
Рельеф Земли. Равнины суши. Горы суши Мой любимый поэт Александр Сергеевич Пушкин
Мой любимый поэт Александр Сергеевич Пушкин Дисперсті жүйелердің оптикалық әдістері
Дисперсті жүйелердің оптикалық әдістері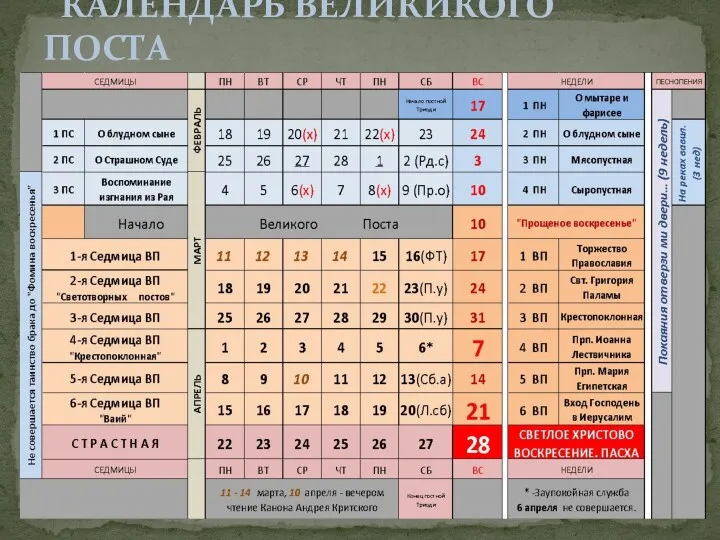 Календарь Великикого Поста
Календарь Великикого Поста Сочинение-описание картины Е. Н. Широкова Друзья
Сочинение-описание картины Е. Н. Широкова Друзья Вольт-амперная характеристика p-n-перехода
Вольт-амперная характеристика p-n-перехода Презентация День защиты детей
Презентация День защиты детей Подвижной состав железных дорог
Подвижной состав железных дорог Коэффициент полезного действия механизма
Коэффициент полезного действия механизма Тізе буыны туберкулезінің салыстырмалы диагностикасы
Тізе буыны туберкулезінің салыстырмалы диагностикасы Технология выращивания посадочного материала. Организация питомника. Лекция-1
Технология выращивания посадочного материала. Организация питомника. Лекция-1