Классификация функций. Предел функции. Бесконечно малые и бесконечно большие функции. (Лекция 3) презентация
Содержание
- 2. Совокупность всех значений независимой переменной, для которых функция определена, называется областью определения или областью существования этой
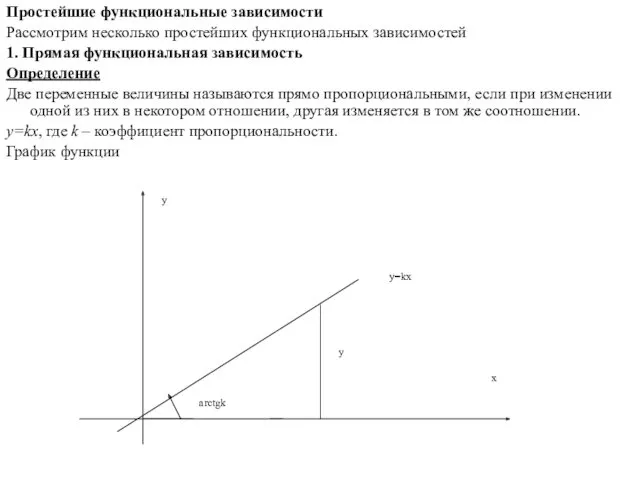
- 3. Простейшие функциональные зависимости Рассмотрим несколько простейших функциональных зависимостей 1. Прямая функциональная зависимость Определение Две переменные величины
- 4. 2. Линейная зависимость Определение Две переменные величины связаны линейной зависимостью, если , где - некоторые постоянные
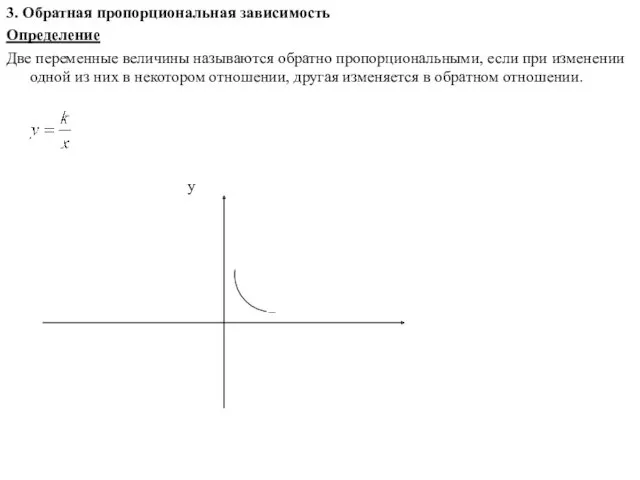
- 5. 3. Обратная пропорциональная зависимость Определение Две переменные величины называются обратно пропорциональными, если при изменении одной из
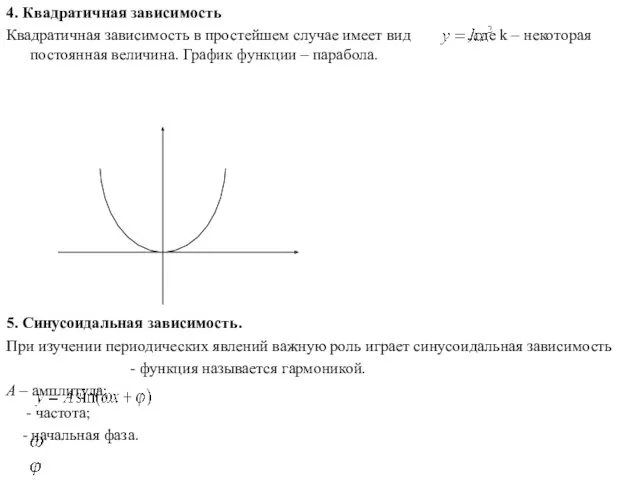
- 6. 4. Квадратичная зависимость Квадратичная зависимость в простейшем случае имеет вид , где k – некоторая постоянная
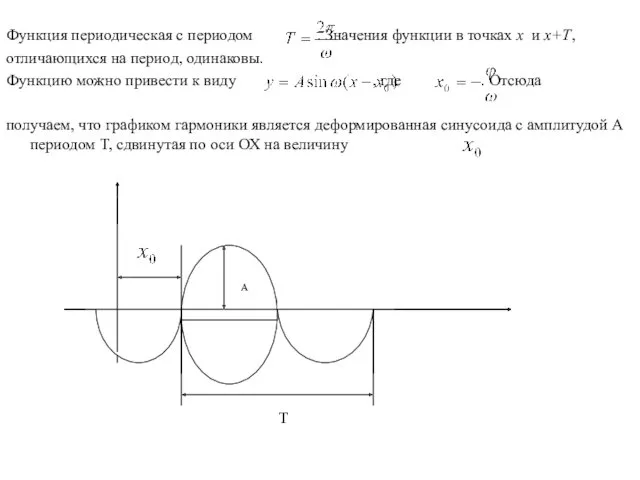
- 7. Функция периодическая с периодом . Значения функции в точках x и x+T, отличающихся на период, одинаковы.
- 8. Способы задания функции Обычно рассматривают три способа задания функции: аналитический, табличный, графический. 1. Аналитический способ задания
- 9. Этого недостатка лишен графический способ задания функции y=f(x), когда соответствие между аргументом x и функцией y
- 10. Классификация функций одного аргумента Принята следующая классификация: 1. Целая рациональная функция или многочлен Над аргументом выполняются
- 11. 5. Трансцендентные функции Всякая неалгебраическая функция называется трансцендентной. Элементарные трансцендентные функции: а) показательная ; b) логарифмическая
- 12. Пример f(x)=sinx отображает интервал на отрезок [-1,1]. Пусть между элементами множеств X и Y функция y=f(x)
- 13. Пусть функция f(x) задана на множестве X. Точка а называется предельной точкой (точкой накопления) этого множества,
- 14. Определение 3 Число А называется пределом функции f(x) при , то есть , если - окрестность
- 15. Определение 5 Функция f(x) называется ограниченной на данном множестве Х, если существует такое положительное число М,
- 16. Введем понятия левой и правой окрестностей точки а (а – число). Определение 1 1) любой интервал
- 17. Замечание Для существования предела функции f(x) при (а – число) необходимо и достаточно выполнение равенства f(a-0)=f(a+0).
- 18. Бесконечно малые функции Определение Функция называется бесконечно малой при (а – вещественное число или символ ),
- 19. Бесконечно большие функции Определение Функция f(x) называется бесконечно большой при (а – число или символ при
- 20. Пусть . В силу определения бесконечно малой функции существуют три, характеризуемые окрестности , такие что при
- 21. Доказательство Пусть при , где - некоторая окрестность точки а и при . Тогда , что
- 23. Скачать презентацию






![Пример f(x)=sinx отображает интервал на отрезок [-1,1]. Пусть между элементами](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/72728/slide-11.jpg)









 Этика и деонтология в онкологии
Этика и деонтология в онкологии Что нужно знать о туберкулезе для личной безопасности?
Что нужно знать о туберкулезе для личной безопасности? Презентация к занятию Чайный сервиз
Презентация к занятию Чайный сервиз Места обитания, классификация зайцев
Места обитания, классификация зайцев Мои увлечения Мои наряды , мой стиль.
Мои увлечения Мои наряды , мой стиль. Организация хранения и транспортировки ЛС, ИМН и медицинской техники
Организация хранения и транспортировки ЛС, ИМН и медицинской техники Презентация Круг семейного чтения
Презентация Круг семейного чтения Урок Простые вещества - металлы
Урок Простые вещества - металлы Ваше тело имеет на вас право
Ваше тело имеет на вас право Творчество Мариуса Ивановича Петипа
Творчество Мариуса Ивановича Петипа Предмет и содержание курса медицинского снабжения Вооружённых Сил РК
Предмет и содержание курса медицинского снабжения Вооружённых Сил РК Токовые защиты. Принцип действия и классификация токовых защит
Токовые защиты. Принцип действия и классификация токовых защит Классный час Композиторы Кубани
Классный час Композиторы Кубани Теории происхождения нефти и газа – основа прогнозирования перспектив нефтеносности недр
Теории происхождения нефти и газа – основа прогнозирования перспектив нефтеносности недр Решение неравенств, содержащих переменную под знаком модуля
Решение неравенств, содержащих переменную под знаком модуля Микроклимат палатки
Микроклимат палатки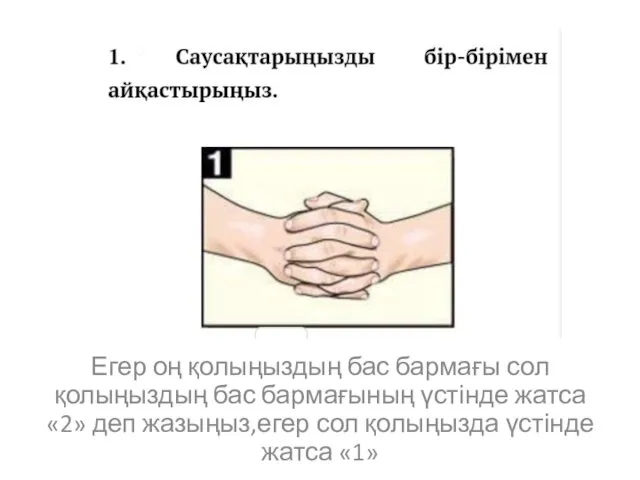 Саусақтарыңызды бір-бірімен айқастырыңыз
Саусақтарыңызды бір-бірімен айқастырыңыз Закаливание. Методы закаливания
Закаливание. Методы закаливания Шаблон для презентаций Ко Дню Победы зеленый
Шаблон для презентаций Ко Дню Победы зеленый Православная позиция
Православная позиция Использование оффшоров в международном менеджменте
Использование оффшоров в международном менеджменте Подставка для яйца на Пасху (зайка) Диск
Подставка для яйца на Пасху (зайка) Диск Нанотехнологии - технологии будущего
Нанотехнологии - технологии будущего Способы эксплуатации нефтяных и газовых скважин
Способы эксплуатации нефтяных и газовых скважин Агрессия как социально-психологический феномен
Агрессия как социально-психологический феномен Символизм. Основные темы символистов
Символизм. Основные темы символистов OZoWS_GZUQaNOQ1uP_qq2A (1)
OZoWS_GZUQaNOQ1uP_qq2A (1) Народные промыслы - Городецкая роспись
Народные промыслы - Городецкая роспись