Содержание
- 2. Понятие Метод Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня заданной
- 3. Описание метода
- 4. Описание метода Преимущество метода Ньютона-Рафсона: сходимость* метода касательных Ньютона очень быстрая. Недостаток метода Ньютона-Рафсона: негарантированная сходимость
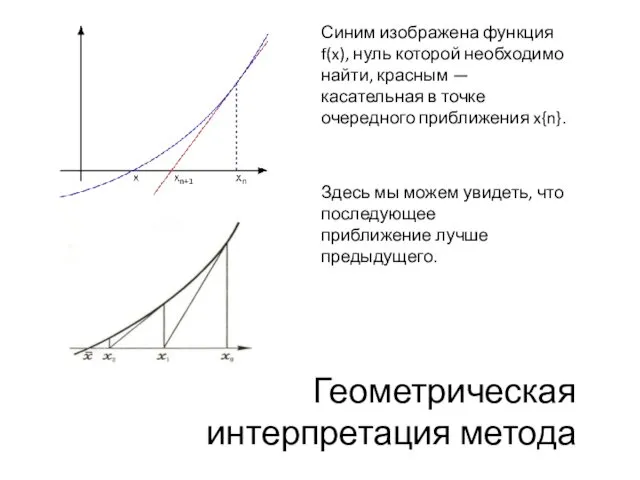
- 5. Геометрическая интерпретация метода Синим изображена функция f(x), нуль которой необходимо найти, красным — касательная в точке
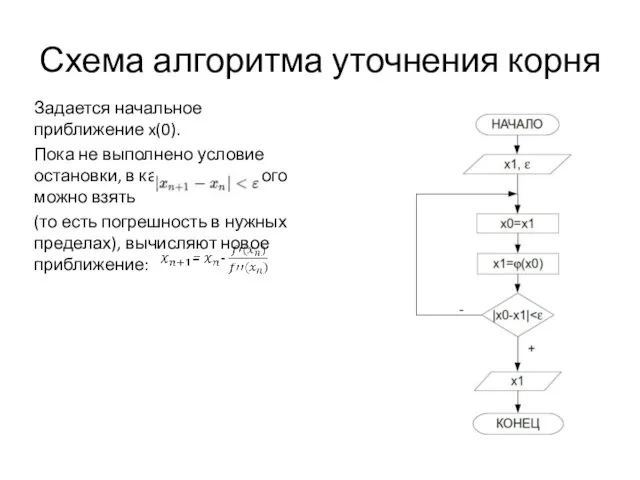
- 6. Схема алгоритма уточнения корня Задается начальное приближение x(0). Пока не выполнено условие остановки, в качестве которого
- 7. Пример
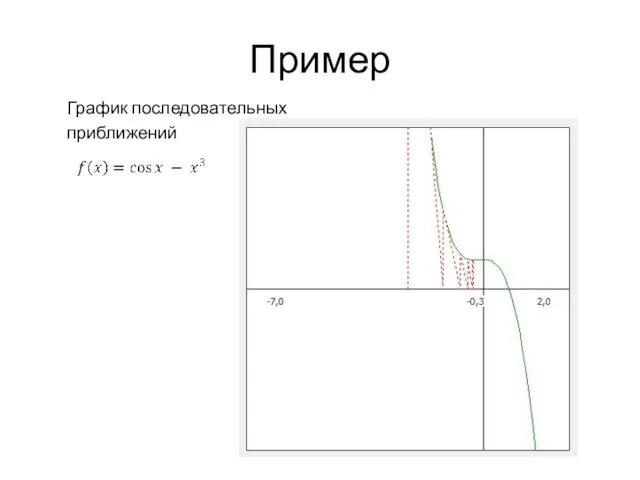
- 8. Пример График последовательных приближений
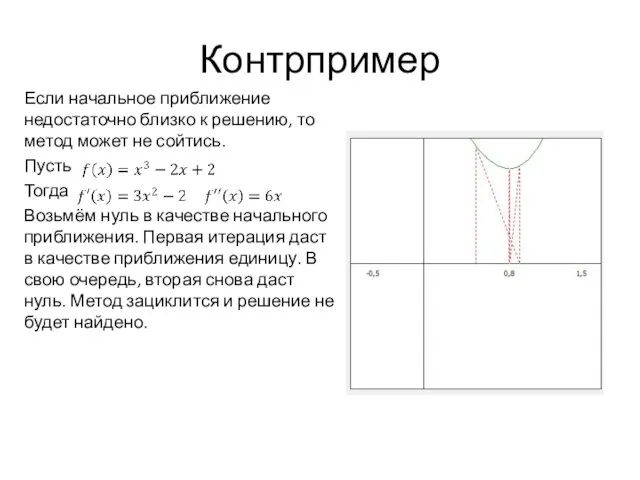
- 9. Контрпример Если начальное приближение недостаточно близко к решению, то метод может не сойтись. Пусть Тогда Возьмём
- 10. Источники https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0 http://matica.org.ua/metodichki-i-knigi-po-matematike/vychislitelnaia-matematika/5-2-1-metod-niutona-rafsona https://dic.academic.ru/dic.nsf/ruwiki/1034652
- 12. Скачать презентацию





 Строительство общеобразовательной школы на 1100 мест в г. Подольске, Московской области
Строительство общеобразовательной школы на 1100 мест в г. Подольске, Московской области Животные Австралии
Животные Австралии портфолио воспитателя Коноваловой Т.А.
портфолио воспитателя Коноваловой Т.А. Введение в информатику. Интернет
Введение в информатику. Интернет Инструкция по обновлению программного обеспечения планшета МегаФон V9+
Инструкция по обновлению программного обеспечения планшета МегаФон V9+ Простые дроби. 6 класс
Простые дроби. 6 класс Презентация для детей Что я знаю о цвете
Презентация для детей Что я знаю о цвете Жизнь в эпоху постправды: понимать или бороться и преодолевать?
Жизнь в эпоху постправды: понимать или бороться и преодолевать? ОбъединениеЮный языковед Диск
ОбъединениеЮный языковед Диск герои - земляки
герои - земляки Встраиваемые микроволновые печи
Встраиваемые микроволновые печи Акулы
Акулы Швейцарский лингвист Фердинанд де Соссюр ( 26 ноября 1857, Женева — 22 февраля 1913)
Швейцарский лингвист Фердинанд де Соссюр ( 26 ноября 1857, Женева — 22 февраля 1913) Разработка урока Природные зоны Южной Америки
Разработка урока Природные зоны Южной Америки Организация предметно-развивающей среды в сенсомоторном развитии детей младшего возраста.
Организация предметно-развивающей среды в сенсомоторном развитии детей младшего возраста. Блюхер Василий Константинович
Блюхер Василий Константинович Первые шаги в науку. Веселое путешествие
Первые шаги в науку. Веселое путешествие Причастие. Иконы
Причастие. Иконы Библия
Библия Презентация Первоцветы
Презентация Первоцветы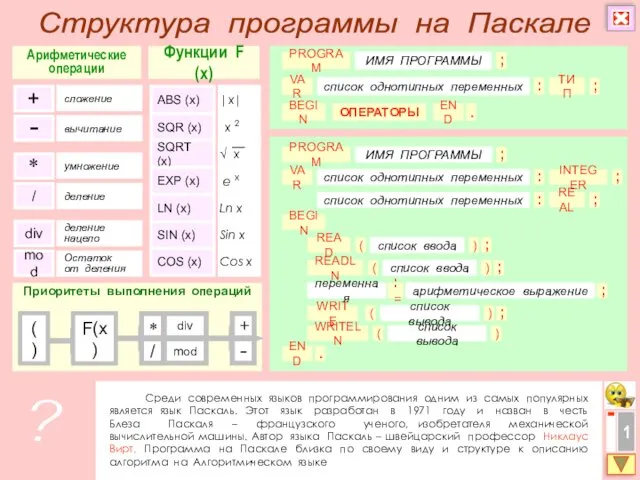 Структура программы на Паскале
Структура программы на Паскале Способ приведения матрицы к ступенчатому виду
Способ приведения матрицы к ступенчатому виду Джанни Родари Джельсомино в Стране Лжецов. Викторина
Джанни Родари Джельсомино в Стране Лжецов. Викторина Методические рекомендации по построению предметно-развивающей среды в соответствии с ФГОС в группе раннего возраста.
Методические рекомендации по построению предметно-развивающей среды в соответствии с ФГОС в группе раннего возраста. Резкость изображения
Резкость изображения Векторы. Что такое вектор и как его обазначают
Векторы. Что такое вектор и как его обазначают Путешествие с комнатными растениями
Путешествие с комнатными растениями Устройство телевидения и его история
Устройство телевидения и его история