Содержание
- 2. СЛОЖНАЯ ФУНКЦИЯ – функция, представленная как композиция нескольких функций. Сложная функция – функция от функции. Сложная
- 3. В композиции может быть и больше двух функций: Чтобы найти производную сложной функции, нужно 1. Определить,
- 4. Функция промежуточного аргумента – квадратичная функция Функция квадратного корня Показательная функция Функция промежуточного аргумента – квадратичная
- 5. Проверим, принадлежит ли х=ln3 промежутку [1; 2] 3 ln Найдите наименьшее значение функции y = e2x
- 6. Найдите наибольшее значение функции 2. x = – 2 Найдем критические точки, которые принадлежат D(у). Вычислим
- 7. При решении некоторых заданий на вычисление наибольшего и наименьшего значений функции можно найти ответ и без
- 8. Найдите наибольшее значение функции 2. 2 способ Решим задание без вычисления производной. Функция квадратного корня монотонно
- 9. Найдите наименьшее значение функции 3. x = 3 Найдем критические точки, которые принадлежат D(у). Вычислим производную,
- 10. Найдите наименьшее значение функции 3. 2 способ Решим задание без вычисления производной. Функция квадратного корня монотонно
- 11. Найдите наименьшее значение функции 4. x = - 1 Найдем критические точки, которые принадлежат D(у). Вычислим
- 12. Найдите наименьшее значение функции 4. Решим задание без вычисления производной. Показательная функция с основанием 2>1 монотонно
- 13. Найдите наибольшее значение функции 5. x = - 3 Найдем критические точки, которые принадлежат D(у). Вычислим
- 14. Найдите наибольшее значение функции 5. 2 способ Решим задание без вычисления производной. Показательная функция с основанием
- 15. Найдите наибольшее значение функции 6. Решим задание без вычисления производной. Логарифмическая функция с основанием 5 является
- 17. Скачать презентацию



![Проверим, принадлежит ли х=ln3 промежутку [1; 2] 3 ln Найдите](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/83473/slide-4.jpg)










 Происхождение галактик
Происхождение галактик Выставка Зимняя сказка
Выставка Зимняя сказка Осеннее ассорти
Осеннее ассорти Зимние загадки для 1 класса
Зимние загадки для 1 класса Вырасти чудо-цветок своими руками
Вырасти чудо-цветок своими руками Аппликация из ткани. Кошки. 4 класс.
Аппликация из ткани. Кошки. 4 класс. Мы теперь ученики!
Мы теперь ученики! Мероприятие по химии посвященное 300 летию со дня рождения М. В. Ломоносова
Мероприятие по химии посвященное 300 летию со дня рождения М. В. Ломоносова Программа кружковой деятельности Говорушка
Программа кружковой деятельности Говорушка 20181225_prezentatsiya_halk
20181225_prezentatsiya_halk Заповеди здорового образа жизни для детей
Заповеди здорового образа жизни для детей Задание 40 и Устная часть 4 (1)
Задание 40 и Устная часть 4 (1)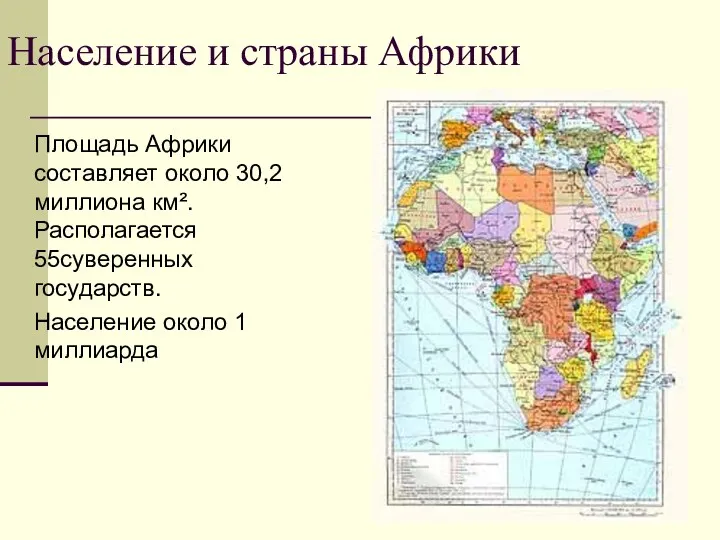 7 класс: Население и государства Африки
7 класс: Население и государства Африки Быт казачьей семьи
Быт казачьей семьи Проект Слава Победе!
Проект Слава Победе! Краткие сведения о канализации
Краткие сведения о канализации Профилактика вредных привычек у детей
Профилактика вредных привычек у детей Применение алгоритмов
Применение алгоритмов Презентация к классному часу Горячее сердце 2014
Презентация к классному часу Горячее сердце 2014 Наше радио
Наше радио Мультимедийная журналистика. Графическая модель
Мультимедийная журналистика. Графическая модель Оториноларингологияның маңызды сұрақтары
Оториноларингологияның маңызды сұрақтары Задержка мочеиспускания
Задержка мочеиспускания Маленькая страна (презентация)
Маленькая страна (презентация) Путешествие на Планету Добра.
Путешествие на Планету Добра. Путешествие викингов
Путешествие викингов Организация сестринского ухода за детьми с дистрофиями. Роль медицинской сестры
Организация сестринского ухода за детьми с дистрофиями. Роль медицинской сестры Современные автомобили и двигатели
Современные автомобили и двигатели