Содержание
- 2. Примеры. Вычислить интегралы: 1
- 3. Решение:
- 4. 2
- 5. Решение:
- 6. 3
- 7. Решение:
- 8. 2. Метод замены переменной или метод подстановки Метод замены переменной описывается формулой: 1
- 9. Где х=φ(t) – функция, дифференцируемая на рассматриваемом промежутке. Покажем справедливость этой формулы. Найдем производную по t
- 10. Получили одинаковый результат, следовательно по следствию из теоремы Лагранжа левая и правая части выражения (1) отличаются
- 11. Полученная формула показывает, что переходя к новой переменной, достаточно выполнить замену переменной в подынтегральном выражении. Удачная
- 12. Примеры. Вычислить интегралы: 1
- 13. Решение:
- 14. 2
- 15. Решение:
- 16. Теорема. Пусть F(x) – некоторая первообразная для функции f(x). Тогда
- 17. Примеры. Вычислить интегралы: 1
- 18. Решение:
- 19. 2
- 20. Решение:
- 21. 3. Интегрирование по частям Пусть функции u(x) и v(x) определены и дифференцируемы на промежутке Х и
- 22. тоже имеет первообразную на этом промежутке и справедлива формула Тогда функция
- 23. Доказательство: Найдем производную произведения данных функций: Отсюда выражаем второе слагаемое в правой части выражения:
- 24. Слагаемые в правой части имеют первообразную на промежутке Х по условию теоремы, следовательно, левая часть тоже
- 25. Поскольку То последнее равенство часто записывают в виде: формула интегрирования по частям
- 26. Примеры. Вычислить интегралы: 1
- 27. Решение:
- 28. 2
- 29. Решение:
- 30. 3
- 31. Решение:
- 32. Можно показать, что формула интегрирования по частям применима для следующих типов интегралов:
- 34. Скачать презентацию

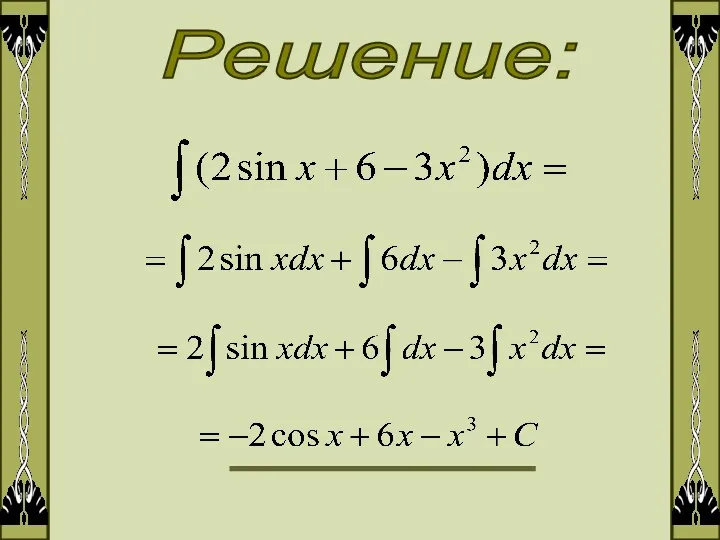


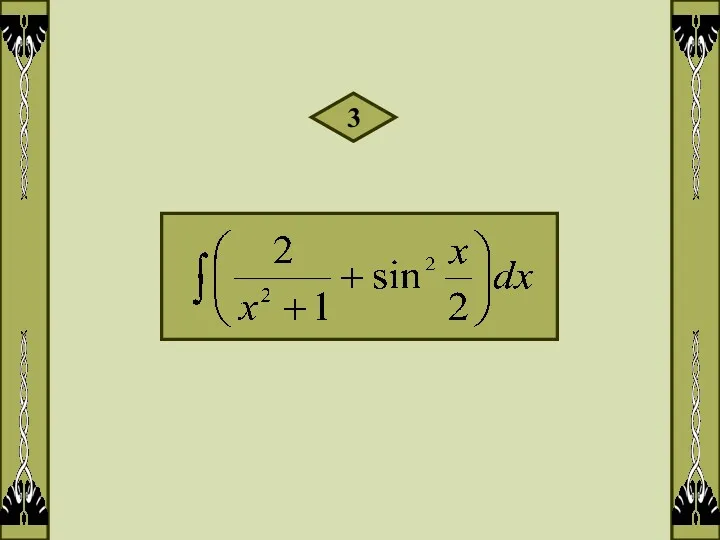
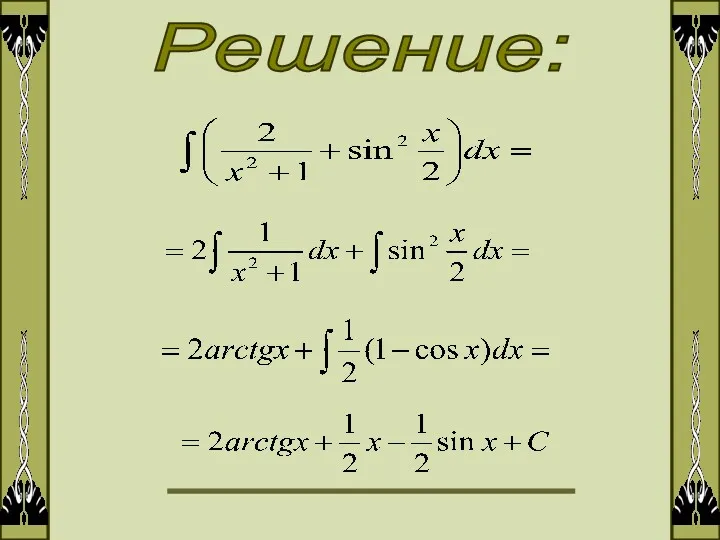





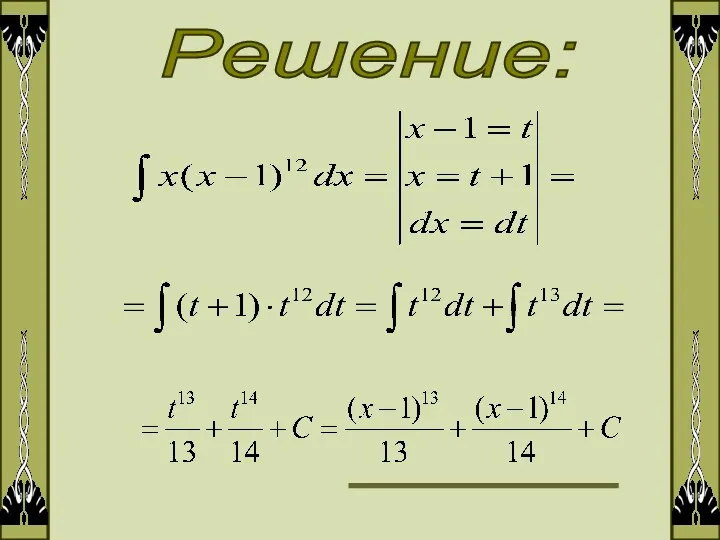
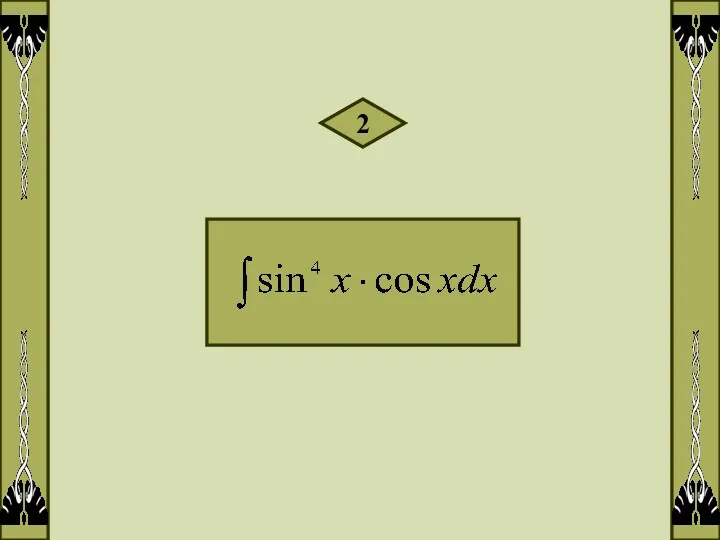
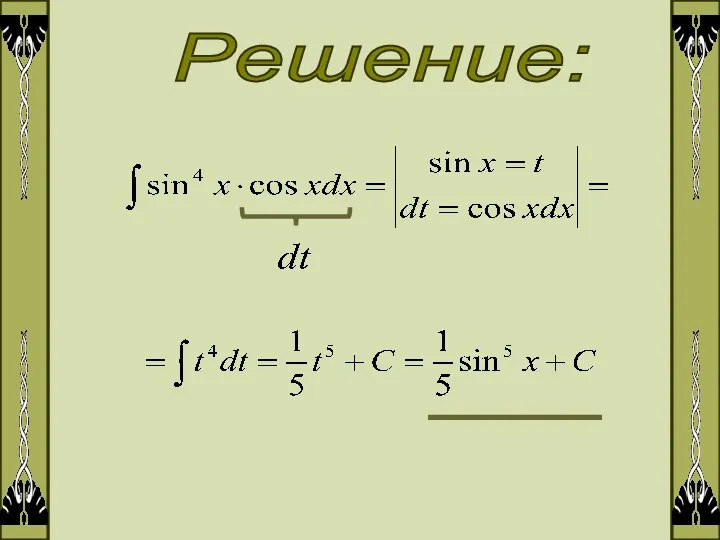


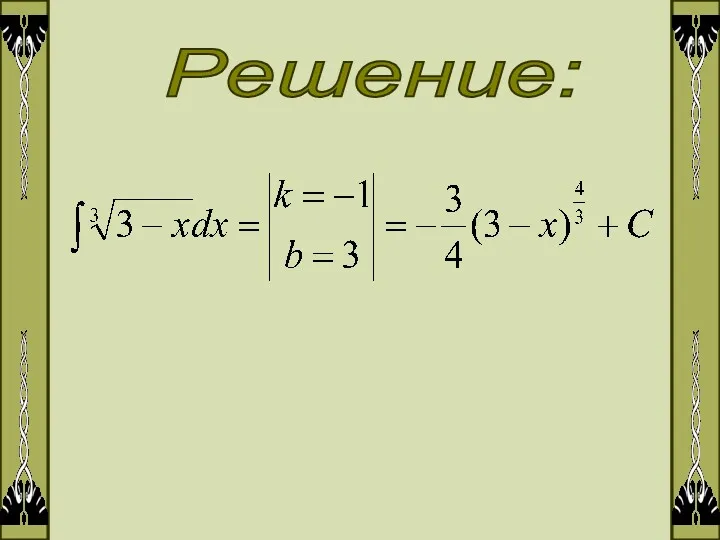
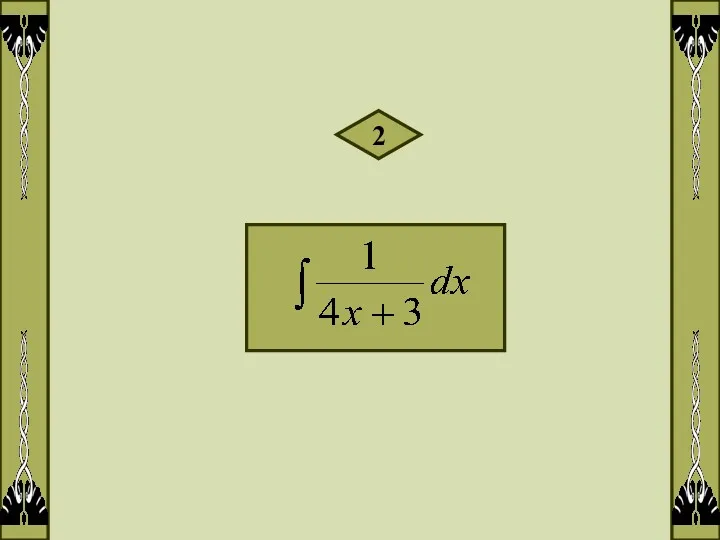
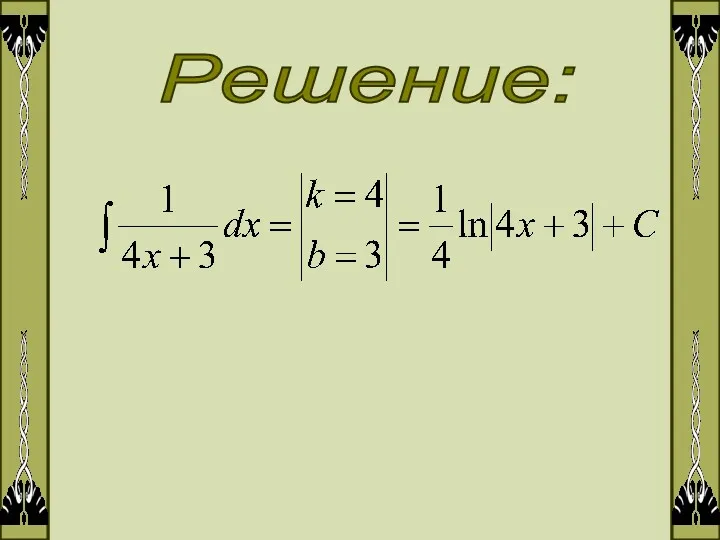






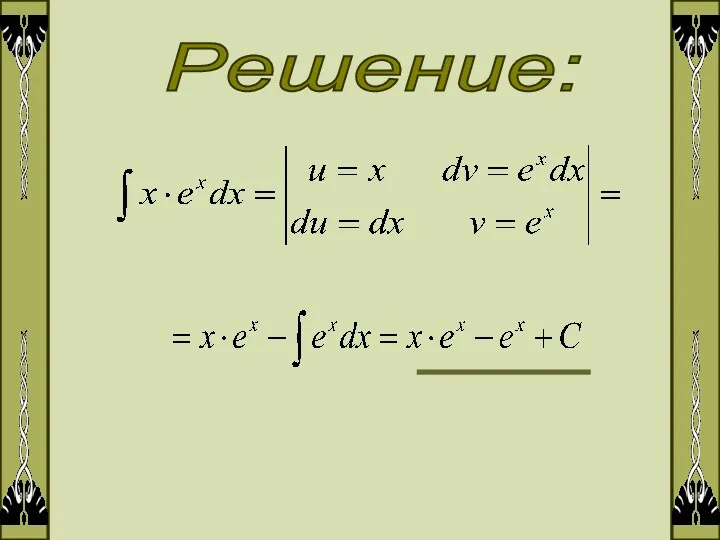
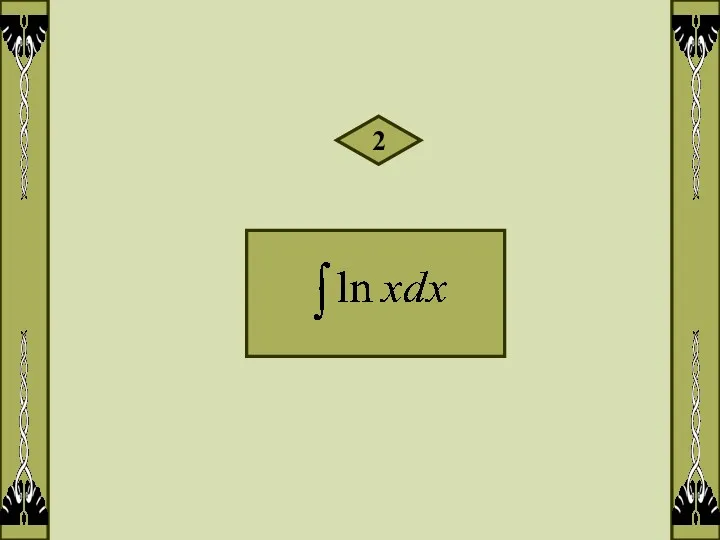
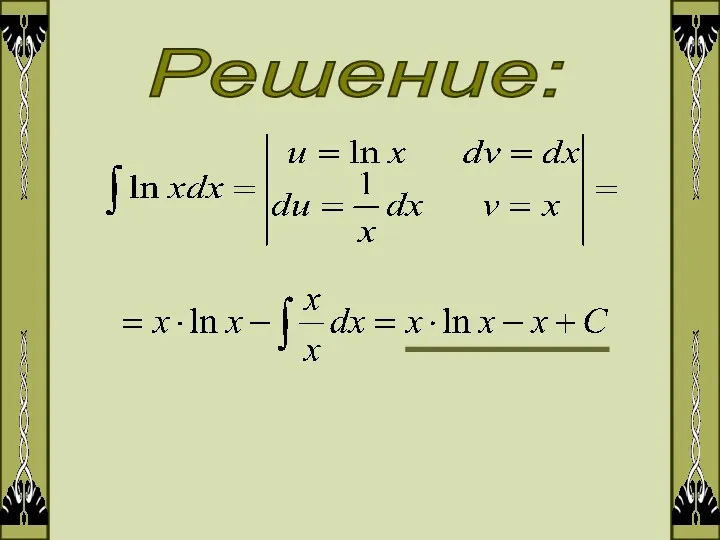
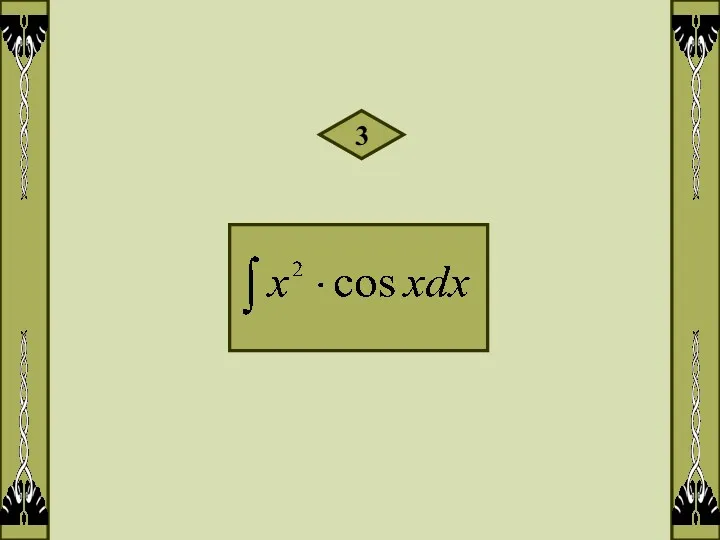
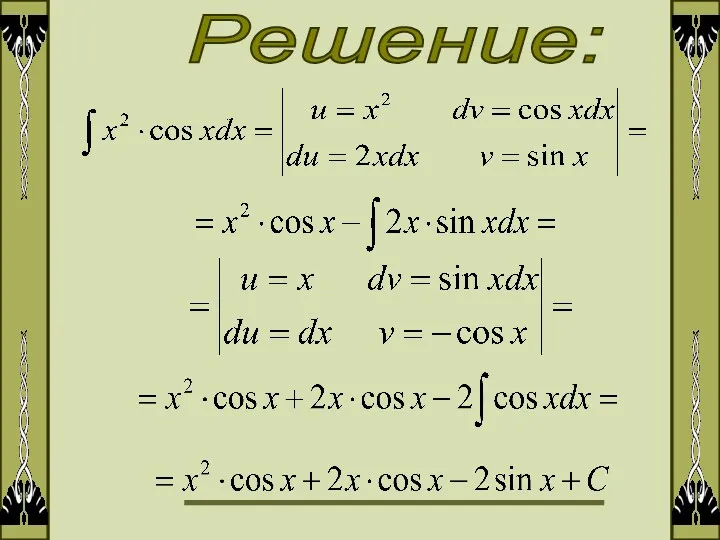

 Презентация Воздушный транспорт
Презентация Воздушный транспорт Инновационные подходы в преподавании физики и при подготовке к государственной итоговой аттестации в форме ЕГЭ и ОГЭ
Инновационные подходы в преподавании физики и при подготовке к государственной итоговой аттестации в форме ЕГЭ и ОГЭ Информация по сессии в Международном юридическом институте
Информация по сессии в Международном юридическом институте Презентация Информационно-коммуникационные технологии в процессе развития и обучения дошкольников
Презентация Информационно-коммуникационные технологии в процессе развития и обучения дошкольников Друзья-лицеисты Пушкина
Друзья-лицеисты Пушкина презентация Готовимся к школе
презентация Готовимся к школе Игровые технологии в ДОУ
Игровые технологии в ДОУ Великий канон cвятого Андрея Критского, читаемый в четверг пятой седмицы Великого поста
Великий канон cвятого Андрея Критского, читаемый в четверг пятой седмицы Великого поста Классный час Моя малая Родина.
Классный час Моя малая Родина. United Kingdom
United Kingdom Интегрированный урок (математика-география) Применение теоремы Пифагора в сельском хозяйстве
Интегрированный урок (математика-география) Применение теоремы Пифагора в сельском хозяйстве Анализ эмитента на примере ПАО ЛУКОЙЛ
Анализ эмитента на примере ПАО ЛУКОЙЛ Математика, как наука
Математика, как наука Технология сборки двутавровой балки
Технология сборки двутавровой балки ЛЕКЦИЯ 8. Электрические машины постоянного тока. Устройство электрической машины постоянного тока
ЛЕКЦИЯ 8. Электрические машины постоянного тока. Устройство электрической машины постоянного тока Информационная культура. Этические и правовые нормы информационной деятельности челове
Информационная культура. Этические и правовые нормы информационной деятельности челове Формирование и развитие философии науки
Формирование и развитие философии науки БЕЗОПАСНОСТЬ НА ДОРОГАХ
БЕЗОПАСНОСТЬ НА ДОРОГАХ 20 способов провалить интервью в Google
20 способов провалить интервью в Google Музеи мира. Лувр
Музеи мира. Лувр История основания города Петрозаводска
История основания города Петрозаводска Соуси
Соуси Типы и конструкции микроэлектромеханических систем. Сенсоры. Классификация сенсоров
Типы и конструкции микроэлектромеханических систем. Сенсоры. Классификация сенсоров ПЕДАГОГИЧЕСКИЙ СОВЕТ НА ТЕМУ: Формирование правовой компетентности учащихся – предупреждение подростковой преступности и правонарушений.
ПЕДАГОГИЧЕСКИЙ СОВЕТ НА ТЕМУ: Формирование правовой компетентности учащихся – предупреждение подростковой преступности и правонарушений. Учитель года-2012
Учитель года-2012 Преступления против собственности
Преступления против собственности Учимся рисовать вместе. Советы для родителей
Учимся рисовать вместе. Советы для родителей Сообщающиеся сосуды
Сообщающиеся сосуды