Слайд 2

Задачи математической статистики
Установление закономерностей, которым подчинены массовые случайные явления, основано
на изучении методами теории вероятностей статистических данных — результатов наблюдений.
Слайд 3

Первая задача математической статистики — указать способы сбора и группировки статистических
сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики—разработать методы анализа статистических данных в зависимости от целей исследования.
Слайд 4

Задача математической статистики состоит в создании методов сбора и обработки статистических
данных для получения научных и практических выводов.
Слайд 5

Генеральная и выборочная совокупности
Выборочной совокупностью или просто выборкой называют совокупность
случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.
Слайд 6

Пример
Если из 1000 деталей отобрано для обследования 100 деталей, то объем
генеральной совокупности N = 1000, а объем выборки n =100.
Слайд 7

Повторная и бесповторная выборки. Репрезентативная выборка
Повторной называют выборку, при которой отобранный
объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается. На практике обычно пользуются бесповторным случайным отбором.
Слайд 8

Свойства объектов выборки должны правильно отражать свойства объектов генеральной совокупности, или,
как говорят, выборка должна быть репрезентативной (представительной). Считается, что выборка репрезентативна, если все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку, т. е. выбор осуществляется случайно.
Слайд 9

Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка, причем х1 наблюдалось
n1 раз, х2 — n2 раз, ..., хk —nk раз и n1 + n2 + … + nk = n— объем выборки. Наблюдаемые значения x1, x2, … xk называются вариантами, а последовательность вариант, записанная в возрастающем порядке — вариационным рядом.
Слайд 10

Числа наблюдений n1, n2, … nk называют частотами, а их отношения
к объему выборки
— относительными частотами. Отметим, что сумма относительных частот равна единице:
Слайд 11

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или
относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал.
Слайд 12

Пример
Дана выборка:
12,2,6,2,6,12,6,2,6,12,6,6,12,12,12,6,6,12,6,6
Составить вариационный ряд и статистическое распределение
Слайд 13

Решение
Составим вариационный ряд:
2,2,2,6,6,6,6,6,6,6,6,6,6,12,12,12,12,12,12,12
Создадим статистическое распределение:
Слайд 14

Пример
Задано распределение частот выборки объема n — 20:
Написать распределение относительных
частот.
Слайд 15

Решение
Найдем относительные частоты, для чего разделим частоты на объем выборки:
Поэтому
получаем следующее распределение:
Слайд 16

Полигон и гистограмма
Для графического изображения статистического распределения используются полигоны и гистограммы.
Полигоном
частот называют ломаную, отрезки которой соединяют точки
(х1; n1), (х2; n2), ..., (xk; nk).
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки
Слайд 17

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат
частичные интервалы длиною h, а высоты равны отношению (плотность частоты).
Площадь i-го частичного прямоугольника равна
—сумме частот вариант i-гo интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т. е. объему выборки.
Слайд 18
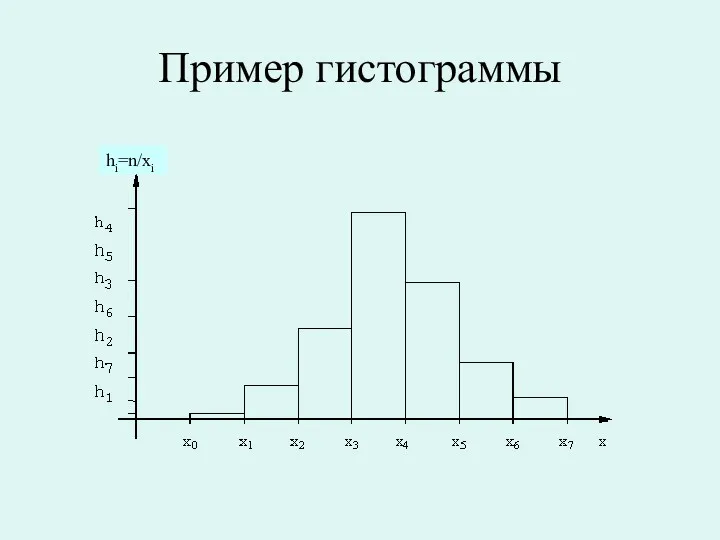
Пример гистограммы
hi=n/xi
Слайд 19

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною h, а высоты равны отношению (плотность относительной частоты).
Площадь i-го частичного прямоугольника равна
- относительной частоте вариант, попавших в i-й интервал, следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.
Слайд 20

Статистические оценки параметров распределения
Cтатистической оценкой неизвестного параметра теоретического распределения называют
функцию от наблюдаемых случайных величин.
Слайд 21

Генеральная и выборочная средние. Методы их расчета .
Пусть изучается дискретная генеральная
совокупность объема N относительно количественного признака X.
Генеральной средней называют среднее арифметическое значений признака генеральной совокупности.
Слайд 22

Если все значения x1, x2, … xN признака генеральной совокупности объема
N различны, то
Если же значения признака x1, x2, … xk имеют соответственно частоты N1, N2, ..., Nk, причем N1 + N2 + ... + Nk = N, то
или
Слайд 23

Пусть для изучения генеральной совокупности относительно количественного признака X произведена выборка
объема n.
Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.
Слайд 24

Если все значения x1, x2, … xk признака выборки объема n
различны, то
Слайд 25

Если же значения признака x1, x2, … xk имеют соответственно частоты
n1, n2 … nk причем n1 + n2 + … +nk = n, то
или
Слайд 26

Генеральная и выборочная дисперсии.
Для того чтобы охарактеризовать рассеяние значений количественного признака
X генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.
Слайд 27

Генеральной дисперсией DГ называют среднее арифметическое квадратов отклонений значений признака генеральной
совокупности от их среднего значения .
Если все значения x1, x2, … xN признака генеральной совокупности объема N различны, то
Слайд 28

Если же значения признака x1, x2, … xk имеют соответственно частоты
N1, N2, ..., Nk, причем N1 + N2 + ... + Nk = N, то
Слайд 29

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:
Слайд 30

Выборочной дисперсией DB называют среднее арифметическое квадратов отклонения наблюдаемых значений признака
от их среднего значения .
Если все значения x1, x2, … xk признака выборки объема n различны, то
Слайд 31

Если же значения признака x1, x2, … xn имеют соответственно частоты
n1, n2 … nk причем n1 + n2 + … +nk = n, то
Слайд 32

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:
Слайд 33

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной
дисперсии не равно оцениваемой генеральной дисперсии, а равно
Слайд 34

Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно
генеральной дисперсии. Достаточно для этого умножить DB на дробь . Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию
Слайд 35

Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше,
— точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Слайд 36

Интервальной называют оценку, которая определяется двумя числами — концами интервала. Интервальные
оценки позволяют установить точность и надежность оценок.
Слайд 37

Пусть X — оцениваемый параметр генеральной совокупности (генеральное среднее, генеральная дисперсия
и т.д.), a — его точечная оценка, полученная по выборке.
Интервальной оценкой параметра X называется оценка вида
Слайд 38

При этом интервал
называется доверительным интервалом.
Величина ε характеризует точность оценки,
а величина Рα равна вероятности того, что параметр лежит в указанных пределах.
Слайд 39

Пусть рассматриваемый признак распределен в генеральной совокупности по нормальному закону с
неизвестными значениями генерального среднего и дисперсии. Для того чтобы получить интервальную оценку генерального среднего Хг, поступают следующим образом.
Слайд 40

Для выборки некоторого объема n вычисляют выборочное среднее и исправленное среднее
квадратическое отклонение .
Выбирают доверительную вероятность Рα (обычно 0,95 или 0,99) и для нее по таблице распределения Стьюдента находят параметр t.
Рассчитывают полуширину доверительного интервала ε:







































 Основы религиозных культур и светской этики
Основы религиозных культур и светской этики интеллектуальная игра
интеллектуальная игра Рефінансування банків
Рефінансування банків Подушка – под ушко
Подушка – под ушко Бренд DUB - Different Unique Boards (Разные Уникальные Доски)
Бренд DUB - Different Unique Boards (Разные Уникальные Доски) Тиристоры
Тиристоры Понятие, функции, виды религии
Понятие, функции, виды религии Химия и повседневная жизнь человека
Химия и повседневная жизнь человека Дни Российских Вин
Дни Российских Вин Нанотехнологии и наноматериалы
Нанотехнологии и наноматериалы Система работы по правилам дорожного движения
Система работы по правилам дорожного движения Вводное занятие по геометрии для учащихся 7 класса
Вводное занятие по геометрии для учащихся 7 класса Ленинский коммунистический союз молодежи РФ
Ленинский коммунистический союз молодежи РФ правила поведения в гололед.
правила поведения в гололед. Древняя Русь в VIII - первой половине XII века
Древняя Русь в VIII - первой половине XII века Птицы (фотографии)
Птицы (фотографии) Основные характеристики и параметры платы Arduino. Подключение и сборка первой схемы
Основные характеристики и параметры платы Arduino. Подключение и сборка первой схемы Моцарт
Моцарт Родительское собрание: Как воспитать уверенность ребёнка в себе
Родительское собрание: Как воспитать уверенность ребёнка в себе Майский праздник - День Победы
Майский праздник - День Победы Проектирование строительного генерального плана
Проектирование строительного генерального плана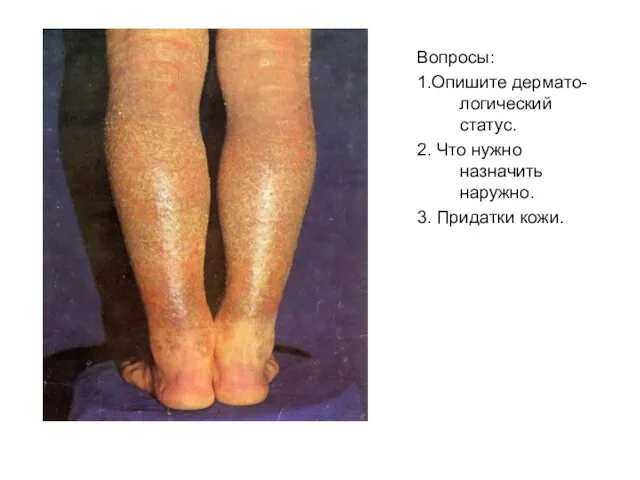 Дерматологический статус
Дерматологический статус Мастер - класс Рисование брызгами
Мастер - класс Рисование брызгами Местное лечение ран. Общее лечение раневой инфекции
Местное лечение ран. Общее лечение раневой инфекции Абарона правоў аўтарам і праваўладальнікам. Вырашэнне спрэчак ў галіне інтэлектуальнай уласнасці
Абарона правоў аўтарам і праваўладальнікам. Вырашэнне спрэчак ў галіне інтэлектуальнай уласнасці Классный час, посвящённый памяти В. Высоцкого.
Классный час, посвящённый памяти В. Высоцкого. Расчетно-графическая работа: отопление дома
Расчетно-графическая работа: отопление дома Дифтерия. Клиническая классификация. Лечение
Дифтерия. Клиническая классификация. Лечение