Содержание
- 2. Стационарен ли временной ряд? Для принятия решения полезно: Смотреть на график временного ряда Использовать формальные статистические
- 3. Тестирование стационарности для AR(1) Н0: θ = 1 – ряд является нестационарным содержит единичный корень; описывается
- 4. Тестирование стационарности для AR(1)
- 5. Обозначим Тестирование стационарности для AR(1)
- 6. Тестирование стационарности для AR(1) Обозначим В этом случае: Н0: θ = 1 ⟹ b =0. Если
- 7. Тестирование стационарности для AR(1) Н0: b = 0 H1: b Идея теста: давайте оценим уравнение обычным
- 8. Тестирование стационарности для AR(1) Н0: b = 0 H1: b Идея теста: давайте оценим уравнение обычным
- 9. Тестирование стационарности для AR(1): тест Дики – Фуллера (DF) Оцениваем уравнение: Н0: b = 0. H1:
- 10. Вычисляем расчетную статистику: Сравниваем расчетное значение с критическим значением из специальных таблиц Дики и Фуллера. Если
- 11. Мы рассмотрели самый простой случай, когда тестируется стационарность AR(1) процесса без константы. В прикладных исследованиях важны
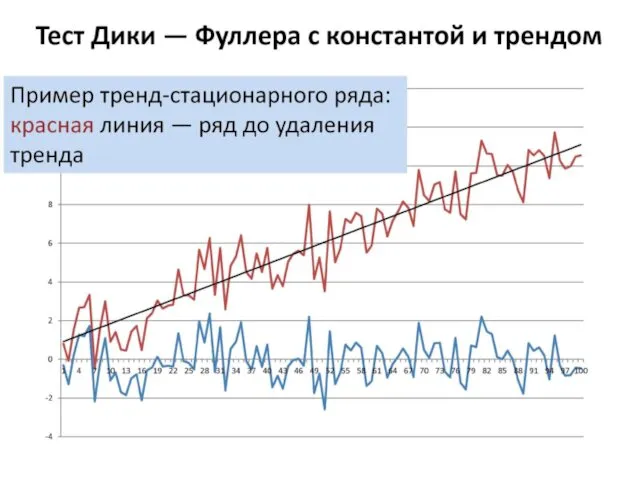
- 12. Тест Дики – Фуллера с константой Н0: θ = 1 – ряд является нестационарным содержит единичный
- 13. Обозначим Оцениваем уравнение Расчетное значение статистики: Сравниваем расчетное значение с критическим значением из специальных таблиц Дики
- 15. Результаты оценивания в Gretl Тест Дики-Фуллера для l_DM Объем выборки 1866 нулевая гипотеза единичного корня: а
- 16. Тест Дики – Фуллера с константой Результаты оценивания в Gretl Тест Дики-Фуллера для l_DM Объем выборки
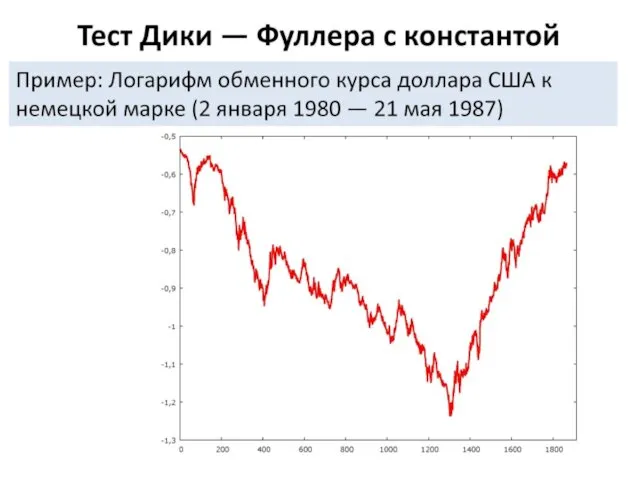
- 17. Тест Дики – Фуллера с константой Пример: Логарифм обменного курса доллара США к немецкой марке (2
- 18. Тест Дики – Фуллера с константой Результаты оценивания в Gretl Тест Дики-Фуллера для l_DM Объем выборки
- 19. Н0: θ = 1 – ряд является нестационарным, описывается процессом случайного блуждания с дрейфом Также в
- 21. Обозначим Оцениваем уравнение Расчетное значение статистики: Сравниваем расчетное значение с критическим значением из специальных таблиц Дики
- 22. Рассмотрим более общий случай авторегрессионного процесса: Н0: ряд является нестационарным, содержит единичный корень Н1: ряд является
- 23. Расширенный тест Дики – Фуллера Оцениваем уравнение: Расчетное значение статистики: Аналогично можно осуществлять ADF-тест с добавлением
- 24. Тест Kwiatkowski, Phillips, Schmidt, Shin (KPSS) Альтернативным тестом для проверки стационарности является KPSS-тест. Н0: Ряд является
- 25. Оцениваем регрессию: Вычисляем остатки Вычисляем вспомогательные суммы (Т штук): Вычисляем расчетное значение статистики: где - оценка
- 26. 5. Если расчетное значение статистики меньше критического значения, равного 0,146, то нулевая гипотеза принимается. Можно сделать
- 27. Рассмотрим решение следующей задачи: Имеется Т наблюдений временного ряда: Необходимо подобрать ARIMA(p,d,q) модель, которая хорошо описывает
- 28. Шаг 1. Определение порядка интегрированности ряда и переход к стационарным разностям Шаг 2. Анализ автокорреляционной функции
- 29. Тестируем ряд на стационарность, используя тесты, которые мы обсудили ранее Если ряд оказался стационарным, то переходим
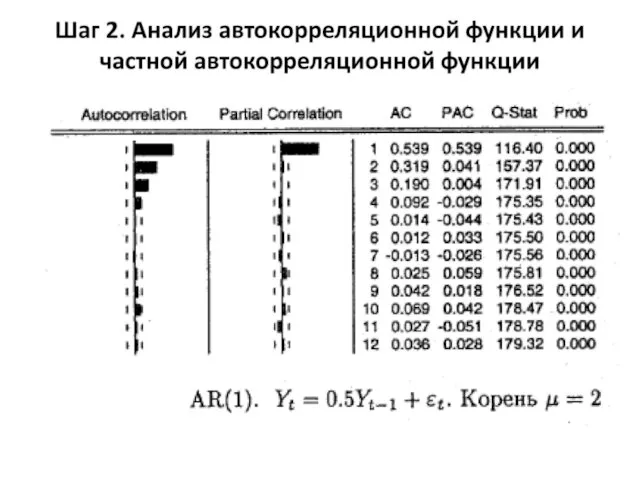
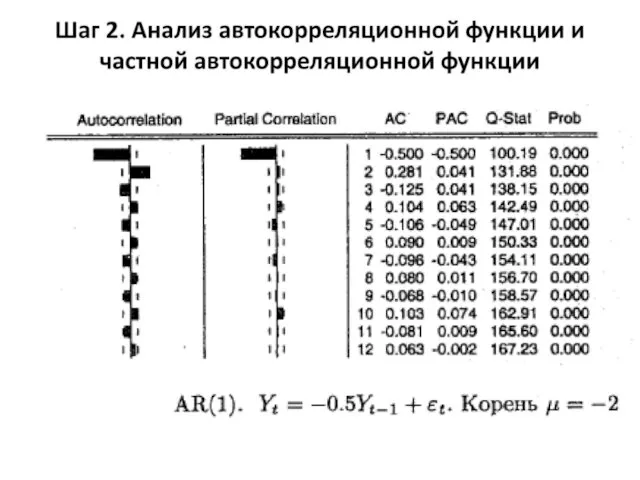
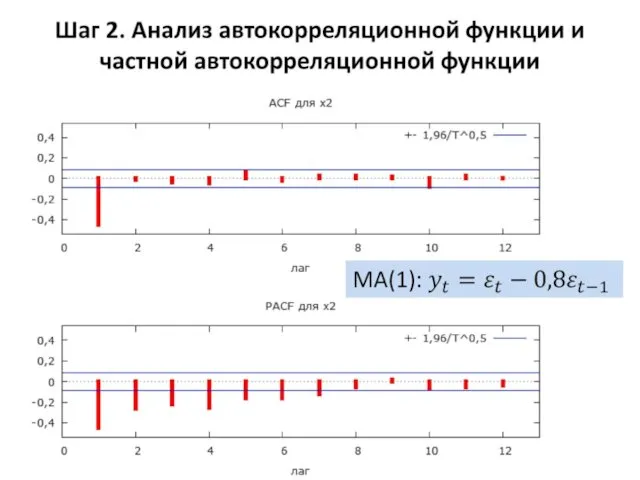
- 30. Шаг 2. Анализ автокорреляционной функции и частной автокорреляционной функции Эмпирическая автокорреляционная функция временного ряда (ACF) –
- 31. Эмпирическая частная автокорреляционная функция временного ряда (PACF) рассчитывается на основе выборочных частных коэффициентов корреляции. Определим выборочный
- 32. На шаге 2 следует построить и проанализировать графики ACF и PACF для рассматриваемого временного ряда. Далее
- 33. Случай А. Процесс AR(p) ACF бесконечна по протяженности и только в пределе при k→∞ сходится к
- 38. Скачать презентацию






























 Презентация для экспертов ТЭК по русскому языку
Презентация для экспертов ТЭК по русскому языку Способы образования имён существительных
Способы образования имён существительных Инженерная академия РУДН
Инженерная академия РУДН материалы курсовой работы по ТРИЗ
материалы курсовой работы по ТРИЗ человеческий капитал
человеческий капитал Илон Ривс. Основатель компаний SpaceX и X.com
Илон Ривс. Основатель компаний SpaceX и X.com Особенности древних цивилизаций. Цивилизации Древнего Востока
Особенности древних цивилизаций. Цивилизации Древнего Востока Российская Федерация: поиск пути развития
Российская Федерация: поиск пути развития Хімічна промисловість в Україні
Хімічна промисловість в Україні Использование здоровьесберегающих технологий для сохранения здоровья подрастающего поколения.
Использование здоровьесберегающих технологий для сохранения здоровья подрастающего поколения. успешность подготовки к ЕГЭ
успешность подготовки к ЕГЭ Энцефалиты. Первичные энцефалиты. Вторичные энцефалиты
Энцефалиты. Первичные энцефалиты. Вторичные энцефалиты Отгадайте загадки
Отгадайте загадки Центр речевой активности в группе ДОУ
Центр речевой активности в группе ДОУ что такое семья
что такое семья Тема урока: Вышивка крестом. Изготовление мешочка из конвы.
Тема урока: Вышивка крестом. Изготовление мешочка из конвы. Нормальная анатомия грудной полости при лучевых исследованиях
Нормальная анатомия грудной полости при лучевых исследованиях Літургійний день ранніх християн
Літургійний день ранніх християн Масленица Диск
Масленица Диск Особенности расследования должностных преступлений
Особенности расследования должностных преступлений Создание учителем условий для приобретения обучающимися позитивного социального опыта
Создание учителем условий для приобретения обучающимися позитивного социального опыта 21 политика
21 политика презентация по теме Атмосфера и климат Земли
презентация по теме Атмосфера и климат Земли Принципы организации службы медицины катастроф
Принципы организации службы медицины катастроф Автоматизированная система для подключения устройств ввода-вывода
Автоматизированная система для подключения устройств ввода-вывода Презентация Керженский заповедник. Нижегородская область
Презентация Керженский заповедник. Нижегородская область Наша достопримечательность: памятник-обелиск, погибшим землякам в поселке Харино
Наша достопримечательность: памятник-обелиск, погибшим землякам в поселке Харино Польза танцев
Польза танцев